Методы глобальной оптимизации
Элементы глобальной оптимизации
Все представленные ранее методы обучения нейронных сетей являются локальными. Они ведут к одному из локальных минимумов целевой функции, лежащему в окрестности точки начала обучения. Только в ситуации, когда значение глобального минимума известно, удается оценить, находится ли найденный локальный минимум в достаточной близости от искомого решения. Если локальное решение признается неудовлетворительным, следует повторить процесс обучения при других начальных значениях весов и с другими управляющими параметрами. Можно либо проигнорировать полученное решение и начать обучение при новых (как правило, случайных) значениях весов, либо изменить случайным образом найденное локальное решение (встряхивание весов) и продолжить обучение сети.
При случайном приращении весов переход в новую точку связан с определенной вероятностью того, что возобновление процесса обучения выведет поиск из "сферы притяжения" локального минимума.
При решении реальных задач в общем случае даже приблизительная оценка глобального минимума оказывается неизвестной. По этой причине возникает необходимость применения методов глобальной оптимизации. Рассмотрим три из разработанных подходов к глобальной оптимизации: метод имитации отжига, генетические алгоритмы и метод виртуальных частиц.
Алгоритмы имитации отжига
Метод имитации отжига основан на идее, заимствованной из статистической механики. Он отражает поведение расплавленного материала при отвердевании с применением процедуры отжига (управляемого охлаждения) при температуре, последовательно понижаемой до нуля.
В процессе медленного управляемого охлаждения, называемого отжигом, кристаллизация расплава сопровождается глобальным уменьшением его энергии, однако допускаются ситуации, в которых она может на какое-то время возрастать (в частности, при подогреве расплава для предотвращения слишком быстрого его остывания). Благодаря допустимости кратковременного повышения энергетического уровня, возможен выход из ловушек локальных минимумов энергии, которые возникают при реализации процесса. Только понижение температуры до абсолютного нуля делает невозможным какое-либо самостоятельное повышение энергетического уровня расплава.
Метод имитации отжига представляет собой алгоритмический аналог физического процесса управляемого охлаждения. Классический алгоритм имитации отжига можно описать следующим образом:
- Запустить процесс из начальной точки
 при заданной
начальной температуре
при заданной
начальной температуре 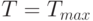 .
. - Пока
 , повторить
, повторить  раз следующие
действия:
раз следующие
действия:- выбрать новое решение
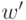 из окрестности
из окрестности  ;
; - рассчитать изменение целевой функции
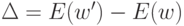 ;
; - если
 , принять
, принять  ; в
противном случае (при
; в
противном случае (при  ) принять, что
) принять, что  с вероятностью
с вероятностью 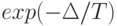 путем генерации
случайного числа
путем генерации
случайного числа  из интервала
из интервала 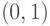 с последующим
сравнением его со
значением
с последующим
сравнением его со
значением 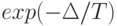 . Если
. Если 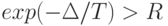 , принять новое решение
, принять новое решение  ;
в противном случае проигнорировать его.
;
в противном случае проигнорировать его.
- выбрать новое решение
- Уменьшить температуру
 с использованием
коэффициента
с использованием
коэффициента  ,
выбираемого из интервала
,
выбираемого из интервала 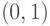 , и вернуться к п. 2.
, и вернуться к п. 2. - После снижения температуры до нуля провести обучение сети любым из детерминированных методов локальной оптимизации вплоть до достижения минимума целевой функции.
Наибольшего ускорения имитации отжига можно достичь путем замены случайных
начальных значений весов  тщательно подобранными значениями с
использованием любых доступных способов предварительной обработки исходных
данных.
тщательно подобранными значениями с
использованием любых доступных способов предварительной обработки исходных
данных.
Метод имитации отжига оказывается особенно удачным для полимодальных комбинаторных проблем с очень большим количеством возможных решений, например, для машины Больцмана, в которой каждое состояние системы считается допустимым. При решении наиболее распространенных задач обучения многослойных нейронных сетей наилучшие результаты в общем случае достигаются применением стохастически управляемого метода повторных рестартов совместно с детерминированными алгоритмами локальной оптимизации.
