Вероятностные и компактные генетические алгоритмы

8.5. Сравнение простых и вероятностных генетических алгоритмов

Для апробации описанных в работе алгоритмов использовались традиционные задачи численной и комбинаторной оптимизации. Рассмотрим полученные результаты более подробно.

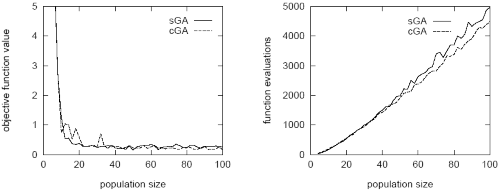
Задачи численной оптимизации (нахождение наибольшего либо наименьшего значения функции многих переменных). Для тестирования использовались функции De Jong 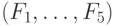. Графическое сравнение эффективности алгоритмов представлено на рис.8.2, из которого видно, что классический и вероятностный ГА дают очень близкие результаты для этого задач численной оптимизации. Однако следует заметить, что вероятностные ГА существенно проще в реализации.

Рис. 8.2. Сравнение простого (sGA) и компактного (cGA) ГА.

Задачи комбинаторной оптимизации.

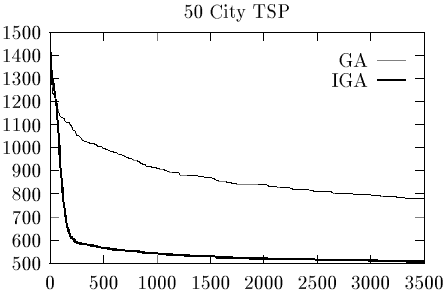
1. Задача коммивояжера (Traveling salesman problem).
   

   
   Рис. 8.3. Сравнение простого (GA) и вероятностного(IGA) ГА.
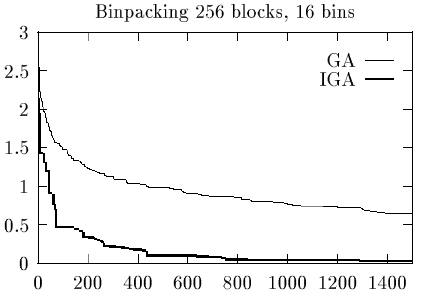
2. Задача упаковки рюкзака (Bin packing).
   

   
   Рис. 8.4. Сравнение простого (GA) и вероятностного(IGA) ГА.
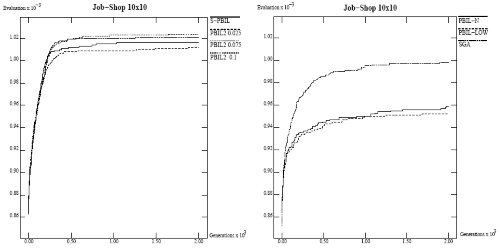
3. Задача календарного планирования (Job-shop scheduling problem).
   

   
   Рис. 8.5. Сравнение простого ГА и различных модификаций PBIL

Аналогично на рис.8.3,рис.8.4,рис.8.5 представлены результаты компьютерных экспериментов, которые показывают близкие характеристики классических и вероятностных ГА для задач комбинаторной оптимизации. Здесь по осям абсцисс отложены число поколений (итераций), а по осям ординат значения фитнесс-функций.

Итак, представленное в графической форме сравнение эффективности работы простого (или классического) ГА с вероятностными и компактными ГА практически однозначно свидетельствует в пользу последних. Более подробное освещение данного вопроса можно найти в первоисточниках [2,3,4]. Генетические алгоритмы в последние годы широко и довольно успешно используются при решении задач численной и комбинаторной оптимизации. Их популярность, в первую очередь, связана с той универсальностью, которая заложена в них теорией эволюции Ч. Дарвина.

Однако, несмотря на значительные преимущества ГА перед остальными метода поиска, приходится констатировать и ряд недостатков. Так, до сих пор не решена проблема преждевременной сходимости ГА к локальным экстремумам. Очередной попыткой, сделанной исследователями в этом направлении, стали вероятностные и компактные ГА. По сравнению с традиционными ГА они имеют ряд преимуществ. Во-первых, это контроль и управление скоростью сходимости генетического поиска. Во-вторых, это поддержка и сохранение разнородности генетической информации в популяции. И, в-третьих, это экономия вычислительных ресурсов. Пока рано говорить о том, что такие ГА полностью решили проблему преждевременной сходимости, однако они существенно сгладили тот негативный эффект, который она создавала. Таким образом, дальнейшие исследования в этой области являются перспективными и вероятностные и компактные ГА при решении практических задач могут быть весьма полезными. Особо следует отметить компактные ГА, которые вследствие своей простоты допускают эффективную аппаратную реализацию. Более полно вероятностные метаэвристики представлены, например, в монографии[7].