Машинное обучение
7.3. Системы классификации XCS
В настоящее время Мичиганский подход к машинному обучению, который позволяет проводить обучение в on-line режиме, получил наибольшее развитие с 1995г. [6,7] в XCS системах. Эти системы, взаимодействуют с неопределенной внешней средой и используют обратную связь в виде поощрения при правильном выборе решения. При этом они стремятся научиться точно прогнозировать размер будущих "премий".
XCS система отличается от традиционных систем машинного обучения (LCS) использованием ГА и другим подходом к определению фитнесс-функции. Во-первых, вычисление фитнесс-функции для классификатора основано на прогнозировании точности величины поощрения, а не на размере самого поощрения. Во-вторых, ГА используется при выборе во множестве возможных действий классификатора, а не при обработке всей популяции. Наконец, в отличие от традиционных систем, XCS не использует список сообщений и поэтому удобна для обучения в среде, воздействие которой моделируется Марковским процессом.
В XCS системах, как и в других машинных системах обучения (LCS), решение проблемы представляется в виде популяции классификаторов. На каждом шаге XCS система принимает конкретное событие из окружающей среды в виде значений сигналов и основываясь на текущих знаниях предлагает решение для этого случая. В зависимости от проблемной ситуации (значений входов) и предложенного решения система определяет численное значение поощрения (премии), которое характеризует качество рекомендуемого решения. В отличие от обычных систем обучения (LCS), где каждому классификатору соответствовала "сила", в XCS системе она фактически заменяется тремя параметрами: 1) (payoff) preduction, 2) prediction error, 3) fitness. Роль этих параметров рассмотрена ниже.
Для простоты мы сначала рассмотрим продукционную систему XCS как систему чистой классификации, в которой распространение поощрения (через обратную связь) необязательно. Однако следует помнить, что XCS является более общей системой обучения, которая способна обучаться итеративно (многошагово), где распространение поощрения для вывода оптимального решения проблемы является обязательным.
Описание проблемы. Рассмотрим задачу классификации на  - множестве двоичных наборов длины
- множестве двоичных наборов длины  . При этом каждая ситуация
. При этом каждая ситуация  характеризуется
характеризуется  двоичными значениями. Целевая концепция приписывает каждой проблемной ситуации соответствующий класс
двоичными значениями. Целевая концепция приписывает каждой проблемной ситуации соответствующий класс  . Двоичные вектора
. Двоичные вектора  , представляющие различные проблемные ситуации, генерируются случайным образом в соответствии с некоторым распределением вероятностей
, представляющие различные проблемные ситуации, генерируются случайным образом в соответствии с некоторым распределением вероятностей  . Если не оговорено специально, то предполагается однородное распределение на всех
. Если не оговорено специально, то предполагается однородное распределение на всех  возможных значениях. Различные ситуации (двоичные вектора
возможных значениях. Различные ситуации (двоичные вектора  ) итеративно предъявляются системе XCS. В соответствие с результатом классификации программа обучения назначает "подкрепление"
) итеративно предъявляются системе XCS. В соответствие с результатом классификации программа обучения назначает "подкрепление"  , отражающее правильность классификации. В простейшем случае нулевое поощрение показывает неправильную классификацию, а ненулевое значение (например, 1000) соответствует правильной классификации.
, отражающее правильность классификации. В простейшем случае нулевое поощрение показывает неправильную классификацию, а ненулевое значение (например, 1000) соответствует правильной классификации.
Представление знаний. Знания представляются популяцией  - множеством классификаторов (правил классификации) по сути в виде дизъюнктивной нормальной формы, где каждый классификатор определяется конъюнктивным термом в дизъюнкции. Таким образом, каждый классификатор можно рассматривать как эксперта в своей проблемной области, который дает в ней экспертное заключение.
- множеством классификаторов (правил классификации) по сути в виде дизъюнктивной нормальной формы, где каждый классификатор определяется конъюнктивным термом в дизъюнкции. Таким образом, каждый классификатор можно рассматривать как эксперта в своей проблемной области, который дает в ней экспертное заключение.
Каждый классификатор состоит из пяти основных компонент и некоторых дополнительных предположений:
- Условная часть
 определяет, когда применим классификатор;
определяет, когда применим классификатор; - Активная часть
 определяет предлагаемую акцию-действие (классификацию или решение);
определяет предлагаемую акцию-действие (классификацию или решение); - Поощрение прогноза
 оценивает среднюю величину "премии" при выполнении действия
оценивает среднюю величину "премии" при выполнении действия  и условия
и условия  ;
; - Ошибка прогноза поощрения
 оценивает среднее абсолютное отклонение
оценивает среднее абсолютное отклонение  относительно реального выигрыша (поощрения;
относительно реального выигрыша (поощрения; - Фитнесс
 оценивает нормированное относительную точность относительно других пересекающихся классификаторов.
оценивает нормированное относительную точность относительно других пересекающихся классификаторов.
Условия классификаторов  представляются строками из
представляются строками из  символов троичного алфавита
символов троичного алфавита ![[\{0,1k,\#\}\ (C\in\{0,1,\#\}^l\dots)]\ \{0,1k,\#\}\ (C\in\{0,1,\#\}^l)](/sites/default/files/tex_cache/35a0d00a8396ec6480d9276f26e5a3dd.png) , где символ # (неопределенность) покрывает значения и 0 и 1 (это 0 или 1, но неизвестно, что именно). Отметим, что C определяет гиперплоскость в булевом
, где символ # (неопределенность) покрывает значения и 0 и 1 (это 0 или 1, но неизвестно, что именно). Отметим, что C определяет гиперплоскость в булевом  -мерном пространстве, в котором классификатор применим. Активная часть определяет одно возможное действие или классификацию. Поощрение прогноза
-мерном пространстве, в котором классификатор применим. Активная часть определяет одно возможное действие или классификацию. Поощрение прогноза  итеративно изменяется в процессе обучения и обеспечивает коррекцию среднего значения "премии" для классификатора в соответствии со значением условной части
итеративно изменяется в процессе обучения и обеспечивает коррекцию среднего значения "премии" для классификатора в соответствии со значением условной части  и выбранного действия
и выбранного действия  . Аналогично выполняется коррекция ошибки прогноза поощрения
. Аналогично выполняется коррекция ошибки прогноза поощрения  и фитнесса
и фитнесса  .
.
Кроме указанных основных компонент, каждый классификатор имеет несколько дополнительных параметров. Размер множества действий  оценивает среднее изменение множества акций. Он изменяется аналогично поощрению прогноза
оценивает среднее изменение множества акций. Он изменяется аналогично поощрению прогноза  . Временной "штамп"
. Временной "штамп"  определяет время, когда последний раз классификатор принимал участие в соревновании при выполнении ГА. Счетчик опыта
определяет время, когда последний раз классификатор принимал участие в соревновании при выполнении ГА. Счетчик опыта  подсчитывает число изменений параметров испытуемого классификатора. Параметр
подсчитывает число изменений параметров испытуемого классификатора. Параметр  определяет число идентичных микроклассификаторов, которые представляет реально данный классификатор.
определяет число идентичных микроклассификаторов, которые представляет реально данный классификатор.
Оценка классификатора. Для текущей проблемной ситуации  система XCS формирует множество соответствий
система XCS формирует множество соответствий ![(match set) [M]](/sites/default/files/tex_cache/4c8c4b6ee2754fc1676ec909cf5c1e76.png) , которое состоит из всех классификаторов в популяции
, которое состоит из всех классификаторов в популяции  , чьи условные части соответствуют
, чьи условные части соответствуют  . По сути, множество соответствий
. По сути, множество соответствий ![[M]](/sites/default/files/tex_cache/73729d04b8e6f0a5d694ba46a855be7e.png) представляет знания о текущей ситуации
представляет знания о текущей ситуации  . Это множество используется для решения проблемы классификации и формирования взвешенных фитнесс-значений поощрений прогноза для каждого варианта возможной классификации. В результате система XCS стремится сформировать полное и точное отображение
. Это множество используется для решения проблемы классификации и формирования взвешенных фитнесс-значений поощрений прогноза для каждого варианта возможной классификации. В результате система XCS стремится сформировать полное и точное отображение  от входных воздействий и акций (действий) в стоимость прогноза, которое позволяет сделать выбор действия с максимальной стоимостью. После выполнения выбранной классификации
от входных воздействий и акций (действий) в стоимость прогноза, которое позволяет сделать выбор действия с максимальной стоимостью. После выполнения выбранной классификации  и результирующего поощрения
и результирующего поощрения  формируется множество действий
формируется множество действий ![[A]](/sites/default/files/tex_cache/7e2bf8880d46cb84f91d8740b2659a88.png) , состоящее из всех классификаторов из
, состоящее из всех классификаторов из ![[M]](/sites/default/files/tex_cache/73729d04b8e6f0a5d694ba46a855be7e.png) , определяемых выбранным действием
, определяемых выбранным действием  . Основные параметры
. Основные параметры  ,
,  и
и  всех классификаторов в
всех классификаторов в ![[A]](/sites/default/files/tex_cache/7e2bf8880d46cb84f91d8740b2659a88.png) корректируются в соответствии со следующими формулами:
корректируются в соответствии со следующими формулами:
 |
( 7.1) |
 |
( 7.2) |
![k=\begin{cases}1,&\text{если $\varepsilon<\varepsilon_0$}\\ \alpha\left(\frac{\varepsilon}{\varepsilon_0}\right)^{-v},&\text{иначе $k'=\frac{k}{\sum_{x\in [A]} k_x}$}\end{cases}](/sites/default/files/tex_cache/c335988d340d7701088417826506fdc1.png) |
( 7.3) |
 |
( 7.4) |
где параметр  - коэффициент обучения,
- коэффициент обучения, 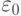 - коэффициент толерантности,
- коэффициент толерантности,  и
и  - дополнительные константы для масштабирования фитнесс-функции. Коэффициент обучения
- дополнительные константы для масштабирования фитнесс-функции. Коэффициент обучения ![\beta\in [0,1]](/sites/default/files/tex_cache/d5476267c79f1cbded0e2d4fad6e37c9.png) определяет точность и адаптивность изменения средней ошибки поощрения прогноза. Высокое значение коэффициента
определяет точность и адаптивность изменения средней ошибки поощрения прогноза. Высокое значение коэффициента  ведет к меньшей зависимости от предыстории и большей адаптивности, но и большей изменчивости вследствие выбора различных значений поощрений. Отметим, что формула (7.1) соответствует коррекции поощрения в
ведет к меньшей зависимости от предыстории и большей адаптивности, но и большей изменчивости вследствие выбора различных значений поощрений. Отметим, что формула (7.1) соответствует коррекции поощрения в  -обучении [8] (которое здесь фактически используется). Однако
-обучении [8] (которое здесь фактически используется). Однако  -значения не аппроксимируются таблицей, а определяются множеством правил, представленных в массиве прогноза
-значения не аппроксимируются таблицей, а определяются множеством правил, представленных в массиве прогноза 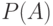 .
.
Значения фитнесс-функции вычисляются согласно формулам (7.3) - (7.4) . Здесь  по сути измеряет текущую абсолютную точность классификатора, используя степенную функцию с параметром
по сути измеряет текущую абсолютную точность классификатора, используя степенную функцию с параметром  в экспоненте для дальнейшего понижения ошибки классификаторов. Порог
в экспоненте для дальнейшего понижения ошибки классификаторов. Порог 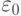 означает порог максимальной толерантности ошибки. В соответствии с этим классификаторы, у которых ошибка
означает порог максимальной толерантности ошибки. В соответствии с этим классификаторы, у которых ошибка  падает ниже порога
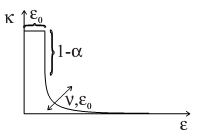
падает ниже порога 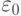 , считаются точными. Отклонение точности
, считаются точными. Отклонение точности  относительно
относительно  показано на рис.7.3. Параметр
показано на рис.7.3. Параметр  управляет степенью падения, параметр
управляет степенью падения, параметр  различает точные и неточные классификаторы.
различает точные и неточные классификаторы.
Относительная точность 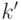 отражает относительную точность по отношению к другим классификаторам в текущем множестве действий
отражает относительную точность по отношению к другим классификаторам в текущем множестве действий  . В действительности каждый классификатор в
. В действительности каждый классификатор в ![[A]](/sites/default/files/tex_cache/7e2bf8880d46cb84f91d8740b2659a88.png) соревнуется за ограниченные ресурсы фитнесса, которые распределяются в зависимости от
соревнуется за ограниченные ресурсы фитнесса, которые распределяются в зависимости от  .
.
Значение фитнесс-функции изменяется согласно формуле (7.4) относительно текущей точности 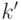 множества действий. Оно отражает изменение средней относительной точности классификатора.
множества действий. Оно отражает изменение средней относительной точности классификатора.
Кроме этого, корректируется параметр  , характеризующий размер множества действий
, характеризующий размер множества действий ![as\leftarrow as+\beta(|[A]|-as)](/sites/default/files/tex_cache/90a990dcadebbf8623a95fc2c5e406a8.png) и чувствительность его изменения в зависимости от коэффициента обучения
и чувствительность его изменения в зависимости от коэффициента обучения  .
.
Эволюция правил. В системе XCS множество правил-классификаторов эволюционирует согласно стационарному ГА с использованием ниш. При этом ниши формируются на основе множества действий классификаторов. Первоначально популяция ![[P]](/sites/default/files/tex_cache/6f585df5b3729ad672d28b2bd7c5b25d.png) пуста. В том случае, когда при предъявлении ситуации
пуста. В том случае, когда при предъявлении ситуации  в
в ![[P]](/sites/default/files/tex_cache/6f585df5b3729ad672d28b2bd7c5b25d.png) нет соответствующих ей классификаторов, используется механизм покрытия, который генерирует классификатор для любой возможной проблемной ситуации. Такой классификатор покрывает данную ситуацию и имеет среднюю определенность
нет соответствующих ей классификаторов, используется механизм покрытия, который генерирует классификатор для любой возможной проблемной ситуации. Такой классификатор покрывает данную ситуацию и имеет среднюю определенность 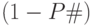 , где
, где  означает вероятность неопределенного символа #. Следует отметить, что если
означает вероятность неопределенного символа #. Следует отметить, что если  имеет значение, близкое к 1, то эволюция стартует с популяции, содержащей слишком общие классификаторы (имеющие в условной части много неопределенных символов), и затем в процессе эволюции происходит снятие неопределенности (замена # на 0 или 1) и вывод более определенных классификаторов. Такой подход чаще применяется на практике. Но возможен и другой подход, при котором эволюция стартует из начальной популяции, содержащей слишком определенные классификаторы (в условной части мало неопределенных символов #). В этом случае в процессе эволюции, наоборот, неопределенные символы вносятся в классификаторы.
имеет значение, близкое к 1, то эволюция стартует с популяции, содержащей слишком общие классификаторы (имеющие в условной части много неопределенных символов), и затем в процессе эволюции происходит снятие неопределенности (замена # на 0 или 1) и вывод более определенных классификаторов. Такой подход чаще применяется на практике. Но возможен и другой подход, при котором эволюция стартует из начальной популяции, содержащей слишком определенные классификаторы (в условной части мало неопределенных символов #). В этом случае в процессе эволюции, наоборот, неопределенные символы вносятся в классификаторы.
В процессе эволюции ГА отбирает два родительских классификатора из текущего множества действий ![[A]](/sites/default/files/tex_cache/7e2bf8880d46cb84f91d8740b2659a88.png) , используя пропорциональный (или турнирный) отбор, где вероятность выбора классификатора
, используя пропорциональный (или турнирный) отбор, где вероятность выбора классификатора  определяется значением относительной фитнесс-функции в
определяется значением относительной фитнесс-функции в ![[A]](/sites/default/files/tex_cache/7e2bf8880d46cb84f91d8740b2659a88.png) , то есть
, то есть
![p_s(cl)=\frac{F(cl)}{\sum_{c\in [A]}F(c)}.](/sites/default/files/tex_cache/9d90653217610cbb043f6e3443482087.png)
Далее генерируются два потомка путем выполнения операторов кроссинговера и мутации. При этом родители остаются в популяции и конкурируют с потомками. Обычно применятся "свободная" мутация, где значение каждого атрибута условной части (имеющее значение из троичного алфавита {0,1,#}) мутирует в одно из двух оставшихся значений (например, неопределенность # в 0 или 1) с равной вероятностью. Иногда применяется мутация в пределах ниши, когда мутировавший классификатор продолжает покрывать (соответствовать) текущую проблемную ситуацию  . Параметры потомков инициализируются путем установки премии прогноза
. Параметры потомков инициализируются путем установки премии прогноза  в текущее значение, и средняя ошибка
в текущее значение, и средняя ошибка  принимает среднее значение во множестве действий. Значения фитнесс-функции и параметра
принимает среднее значение во множестве действий. Значения фитнесс-функции и параметра  приравниваются соответствующим родительским значениям. Дополнительно значение фитнесс-функции потомков уменьшаетсся на 10% по сравнению с родительскими значениями, что отражает пессимистический подход к потомкам. Счетчики
приравниваются соответствующим родительским значениям. Дополнительно значение фитнесс-функции потомков уменьшаетсся на 10% по сравнению с родительскими значениями, что отражает пессимистический подход к потомкам. Счетчики  и
и  устанавливаются в единицу.
устанавливаются в единицу.
Дополнительно в процессе внедрения потомков в популяцию для усиления обобщения классификаторов применяется механизм поглощения. При этом классификаторы–потомки проверяются на возможность поглощения имеющимися классификаторами либо по логике в условной части, либо по точности (в популяции уже есть аналогичные классификаторы с лучшей точностью). Если потомок поглощается имеющимися классификаторами, то он не вносится в популяцию, но увеличивается счетчик num поглощающего классификатора.
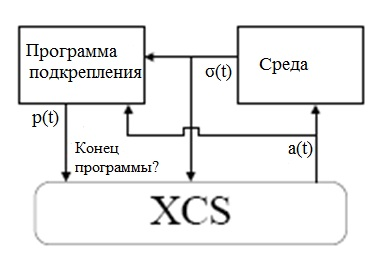
На рис.7.4 представлена общая организация процесса обучения в XCS. Отметим, что в отличие от традиционных систем обучения, система XCS отбирает классификаторы для репродукции из текущего множества действий, определяемого текущей ситуацией  , а не из всей популяции. Кроме этого используются некоторые дополнительные параметры классификаторов и фитнесс-функция основана на оценке точности поощрения прогноза. Сам по себе размер поощрения прогноза меньше влияет на процесс обучения. XCS имеет тенденцию в процессе эволюции генерировать наиболее общее решение проблемы, поскольку при репродукции предпочтение отдается классификатором, которые чаще активны. В целом процесс обучения в XCS направлен на достижение глобальной цели: в результате эволюции получить оптимальное решение проблемы, которое:
, а не из всей популяции. Кроме этого используются некоторые дополнительные параметры классификаторов и фитнесс-функция основана на оценке точности поощрения прогноза. Сам по себе размер поощрения прогноза меньше влияет на процесс обучения. XCS имеет тенденцию в процессе эволюции генерировать наиболее общее решение проблемы, поскольку при репродукции предпочтение отдается классификатором, которые чаще активны. В целом процесс обучения в XCS направлен на достижение глобальной цели: в результате эволюции получить оптимальное решение проблемы, которое:
- является полным, т.е. описывает все области пространства вход/выход;
- не имеет пересечений – ни одна часть пространства не охватывается более одного раза;
- является минимальным, т.е. используется минимальное число непересекающихся правил;
- является максимально точным.
Далее для лучшего понимания рассмотрим простой пример решения задачи классификации для 6-входового мультиплексора.
Обучение XCS на примере мультиплексора.
Этот пример представляет интерес потому, что полное решение проблемы может быть представлено непересекающимися нишами. Функция мультиплексора определяется для двоичных строк длины  , где
, где  –целое число. Для мультиплексора с
–целое число. Для мультиплексора с  входом является двоичная строка из 6 бит, из которых первые две представляют индекс (адрес) а остальные биты являются информационными, один из которых (определяемый адресом) передается на выход. Например, в строке (101101) первые два бита определяют индекс 2, который соответствует предпоследнему биту входной строки и поэтому передается на выход
входом является двоичная строка из 6 бит, из которых первые две представляют индекс (адрес) а остальные биты являются информационными, один из которых (определяемый адресом) передается на выход. Например, в строке (101101) первые два бита определяют индекс 2, который соответствует предпоследнему биту входной строки и поэтому передается на выход  . Аналогично, строка (001000) дает значение выхода
. Аналогично, строка (001000) дает значение выхода 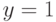 , поскольку первые слева 2 бита определяют индекс 0, указывающий на следующий (третий слева) бит, который и передается на выход. Оптимальное решение для классификации мультиплексора с 6 входами представлено в табл. 7.2.
, поскольку первые слева 2 бита определяют индекс 0, указывающий на следующий (третий слева) бит, который и передается на выход. Оптимальное решение для классификации мультиплексора с 6 входами представлено в табл. 7.2.
| Nr | C | A | R |  |
F |
|---|---|---|---|---|---|
| 1 | 000### | 0 | 1000 | 0 | 1 |
| 2 | 000### | 1 | 0 | 0 | 1 |
| 3 | 001### | 1 | 0 | 0 | 1 |
| 4 | 001### | 1 | 1000 | 0 | 1 |
| 5 | 01#0## | 0 | 0 | 0 | 1 |
| 6 | 01#0## | 1 | 0 | 0 | 1 |
| 7 | 01#1## | 0 | 0 | 0 | 1 |
| 8 | 01#1## | 1 | 1000 | 0 | 1 |
| 9 | 10##0# | 0 | 1000 | 0 | 1 |
| 10 | 10##0# | 1 | 1 | 0 | 1 |
| 11 | 10##1# | 0 | 0 | 0 | 1 |
| 12 | 10##1# | 1 | 1000 | 0 | 1 |
| 13 | 11###0 | 0 | 1000 | 0 | 1 |
| 14 | 11###0 | 1 | 0 | 0 | 1 |
| 15 | 11###1 | 0 | 0 | 0 | 1 |
| 16 | 11###1 | 1 | 1000 | 0 | 1 |
Как отмечалось выше, XCS чаще стартует со множества максимально общих классификаторов (имеющих в условной части много неопределенных символов). В крайнем случае, вероятность неопределенности полагается  , что ведет к тому, что начальная популяция содержит два максимально общих классификатора
, что ведет к тому, что начальная популяция содержит два максимально общих классификатора 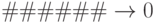 и
и  . Далее в процессе эволюции оператор мутации вносит определенные значения 0 и 1. Однако одного оператора мутации недостаточно, так как слишком общие классификаторы дают большее число множеств акций-действий и необходимо применять оператор кроссинговера. В табл.7.3 показан пример промежуточной популяции классификаторов, в которых классификаторы содержат неопределенные символы. Отметим, что сначала определенные значения ведут к меньшей ошибке и большей точности. Внесение определенности на начальном этапе в адресный или дополнительный бит дает одинаковый либо положительный эффект, либо ошибку.
. Далее в процессе эволюции оператор мутации вносит определенные значения 0 и 1. Однако одного оператора мутации недостаточно, так как слишком общие классификаторы дают большее число множеств акций-действий и необходимо применять оператор кроссинговера. В табл.7.3 показан пример промежуточной популяции классификаторов, в которых классификаторы содержат неопределенные символы. Отметим, что сначала определенные значения ведут к меньшей ошибке и большей точности. Внесение определенности на начальном этапе в адресный или дополнительный бит дает одинаковый либо положительный эффект, либо ошибку.
В целом сначала процесс эволюции способствует внесению большего числа определенных значений. Вскоре, однако, начинает преобладать внесение определенных значений в адресные биты, что способствует генерации полных и точных классификаторов.
| Nr | C | A | R |  |
|---|---|---|---|---|
| 1 | ###### | 0 | 500.0 | 500.0 |
| 2 | ###### | 1 | 500.0 | 500.0 |
| 3 | 1##### | 0 | 500.0 | 500.0 |
| 4 | 1##### | 1 | 500.0 | 500.0 |
| 5 | 0##### | 0 | 500.0 | 500.0 |
| 6 | 1##### | 1 | 500.0 | 500.0 |
| 7 | ##1### | 0 | 375.0 | 468.8 |
| 8 | ##1### | 1 | 625.0 | 468.8 |
| 9 | ##0### | 0 | 625.0 | 468.8 |
| 10 | ##0### | 0 | 375.0 | 468.8 |
| 11 | ##11## | 0 | 250.0 | 375.0 |
| 12 | ##11## | 1 | 750.0 | 375.0 |
| 13 | ##00## | 0 | 250.0 | 375.0 |
| 14 | ##00## | 1 | 750.0 | 375.0 |
| 15 | 0#1### | 0 | 750.0 | 375.0 |
| 16 | 0#1### | 1 | 750.0 | 375.0 |
| 17 | 0#0### | 0 | 750.0 | 375.0 |
| 18 | 0#0### | 1 | 250.0 | 375.0 |
| 19 | 0#11## | 0 | 0.0 | 0.0 |
| 20 | 0#11## | 1 | 1000.0 | 0.0 |
| 21 | 001### | 0 | 0.0 | 0.0 |
| 22 | 001### | 1 | 1000.0 | 0.0 |
| 23 | 10##1# | 0 | 0.0 | 0.0 |
| 24 | 10##1# | 1 | 1000.0 | 0.0 |
| 25 | 000### | 0 | 1000.0 | 0.0 |
| 26 | 000### | 1 | 0.0 | 0.0 |
| 27 | 01#0## | 0 | 1000.0 | 0.0 |
| 28 | 01#0## | 1 | 0.0 | 0.0 |