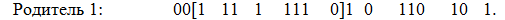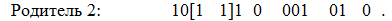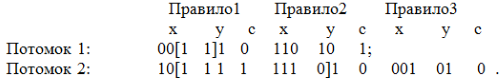Машинное обучение

7.1. Питтсбургский подход

Здесь каждая особь в популяции представляет целый набор правил (а не отдельное правило, как в альтернативном подходе). Как обычно, особи конкурируют между собой, при этом слабые особи умирают, сильные живут и воспроизводятся. Здесь при реализации ГА часто используется пропорциональный отбор родителей, а операторы кроссинговера и мутации определяются над соответствующими структурами данных. Следует отметить, что Питтсбургский подход позволяет избежать тонкой проблемы оценки эффективности отдельного правила, для которой применяются эвристические методы.

Рассмотрим один из возможных способов кодирования правила [4] на примере продукции .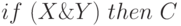

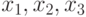Пусть переменная для определенности принимает три значения , а переменная – два значения . Тогда для кодирования значений переменной будем использовать три бита, соответственно для переменной два бита (по одному биту для каждого возможного значения). При этом значение 1 в соответствующей позиции означает, что переменная может принимать соответствующее значение. Например, код (010) для переменной означает, что эта переменная имеет значение . Более того, этот способ кодирования позволяет описывать ситуации, когда переменная может принимать несколько значений [4]. Так код (011) для той же переменной означает, что переменная может принимать значения 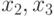. Отметим, что код (111) соответствует наименьшим ограничениям, когда переменная может принимать любые (из допустимых) значения. Тогда, например, гипотеза (концепция) кодируется следующим образом (110 1). Данный метод кодирования позволяет легко учитывать ограничения на значения нескольких атрибутов (переменных) путем конкатенации (сцепления) двоичных кодов этих переменных. Так, например, гипотеза 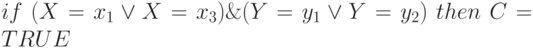кодируется двоичной строкой (101 11 1). Следует отметить, что двоичная строка, представляющая некоторое правило–продукцию, содержит для каждого атрибута (переменной) соответствующую подстроку (даже в том случае, когда на ее значения не накладываются никаких ограничений – атрибут может принимать любые значения). Это определяет фиксированный размер двоичной строки для кодирования правила–продукции, в котором под кодирование значений каждого атрибута выделяется поле в определенных позициях.

Данный метод кодирования легко распространяется на множество продукций путем конкатенации (сцепления) двоичных строк, которые представляют отдельные продукции [4]. Например, множество продукций (представляющих гипотезы)

можно представить следующей двоичной строкой (001 11 1 111 01 0 110 10 1) в соответствии с тремя правилами .

При Питтсбургском подходе одна двоичная строка представляет (как и в классическом ГА) потенциальное решение – множество продукций. В этом случае популяция, как обычно, содержит множество особей - потенциальных решений (систем продукций). Далее для представленного метода кодирования продукций необходимо определить генетические операторы кроссинговера и мутации. Поскольку система продукций кодируется двоичной строкой, то возможно использование стандартных генетических операторов кроссинговера (например, одноточечного, двухточечного, однородного, которые рассмотрены в разделе 4) и классической мутации. Но для повышения эффективности при реализации данного метода в системе GABIL, в которой применяется данный подход [5], используются следующие модификации генетических операторов.

При рекомбинации применяется двухточечный оператор кроссинговера, который учитывает специфику кодирования, в частности то, что родительские особи могут иметь различную длину. Это оператор выполняется следующим образом. Первая и вторая точка кроссинговера в первом родителе выбирается случайным образом. Пусть обозначает расстояние от левого (правого) края двоичной строки кода правила до первой (второй) точки кроссинговера родительской особи. Во второй родительской особи точки кроссинговера также выбираются случайным образом, но так, чтобы расстояния сохранились. Эти ограничения обусловлены семантикой и методом кодирования системы продукций и позволяет "разрывать" вторую особь так, чтобы сохранялся "формат" представления системы продукций. При этом точка кроссинговера должна попадать на тот же разряд кода той же переменной, но, возможно, другого правила данной системы. Рассмотрим выполнение двухточечного кроссинговера на примере следующих особей:

Допустим, что для первого родителя выбраны точки кроссинговера 2, 10, что соответствует (номер позиции от левого края правила с первой точкой кроссинговера) и 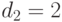(номер позиции от правого края правила со второй точкой кроссинговера) – это показано ниже квадратными скобками [4]:

Тогда возможны следующие варианты выбора пар точек кроссинговера во втором родителе: (2,4), (2,10), (8,10). При этом первая точка кроссинговера попадает между вторым и третьим разрядами двоичного кода переменной , а вторая точка – между первым и вторым разрядами кода переменной . Для определенности возьмем пару точек (2,4), что дает

Далее, как обычно, в двухточечном кроссинговере выполняется обмен фрагментами двоичных кодов между точками кроссинговера (скобками [ и ]), что дает следующих потомков (две новых систем продукций):

Следует отметить, что в результате выполнения такого кроссинговера число правил в системе продукций может изменяться.

Далее к полученным потомкам с небольшой вероятностью применяется один из следующих операторов мутации:

1. стандартный оператор мутации, инвертирующий один двоичный разряд;
2. оператор, изменяющий в случайным образом выбранном разряде нулевое значение на единичное ;
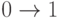3. оператор, который устанавливает все разряды кода выбранной переменной правила в единицу (то есть фактически исключает ее из рассмотрения, поскольку приписывает ей неопределенное значение и она не влияет на результат).

Следует особо отметить, что при Питтсбургском подходе проблема построения фитнесс-функции решается гораздо проще, чем в Мичиганском, поскольку здесь оценивается вся система продукций в целом. Одним из самых распространенных видов фитнесс-функции [2] является следующий:

где 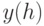– процент правильно классифицируемых примеров обучающей выборки с помощью гипотезы (системы продукций) . При этом каждое потенциальное решение – система продукций оценивается на обучающей выборке "естественным образом".