Генетические алгоритмы многокритериальной оптимизации
5.5. Меры качества решений
Пусть 
множество решений. Для того чтобы оценить эффективность различных подходов к вычислению значений фитнесс-функции для особей, необходимо определить явную меру оценки близости 
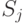к известному множеству оптимального по Парето решению 
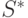. В данном разделе рассмотрены три основные меры, которые, в основном, используются в многокритериальных ГА. Они обеспечивают хорошую оценку сходимости, если известно (суб)оптимальное решение по Парето, что показано на рис.5.13.
Число полученных решений
В простейшем случае в качестве меры 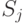можно использовать количество полученных решений 
.
Отношение недоминируемых решений 
В этой мере подсчитывается число решений 
, которые входят в Парето-оптимальное решение 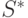и делится на общее число решений следующим образом:
где 
означает, что решение доминируемо решением 
. Отметим, что равенство 
означает, что все решения принадлежат Парето- оптимальному решению 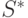. Напротив, равенство 
означает, что ни одно решение не принадлежит Парето-оптимальному решению 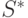. Для достоверности данной меры число полученных решений должно быть достаточно большим. Однако, если некоторое решение не принадлежит 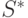, то оно не может быть подсчитано в 
, что является недостатком данной меры.
В этом случае в качестве меры используется среднее расстояние решений 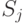от 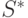, которое определяется следующим образом:
где 
- расстояние между текущим решением и базовым (принадлежащим оптимальному фронту Парето) , которое в случае двух целей вычисляется так:
Чем меньше величина 
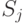, тем лучше решение . В этой мере явным образом подсчитывается близость решени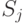й и .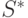
