Генетические алгоритмы многокритериальной оптимизации
5.2. Векторная оценка
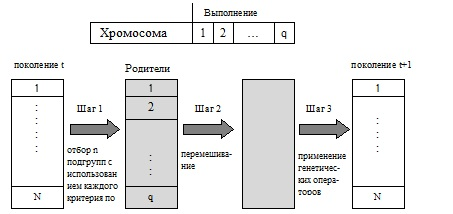
Этот метод является фактически первым эволюционным алгоритмом для решения задач многокритериальной оптимизации. Здесь вместо использования скалярной фитнесс-функции для каждой хромосомы предложено применять векторную фитнесс-функцию. При этом шаг отбора особей реализуется в виде цикла, где каждый раз соответствующая часть (доля популяции или подпопуляций) выбирается на основе каждого из 
критериев. Затем вся популяция полностью смешивается и применяются операторы кроссинговера и мутации. Это делается для того, чтобы достичь скрещивания особей из разных подпопуляций. В процессе эволюции идентифицируются недоминируемые особи в популяции, но эта информация не используется непосредственно в ГА. Такой подход, показанный на рис.5.2, обеспечивает выживание лучших особей относительно каждого критерия и одновременно повышает вероятность кратного выбора особей, которые являются лучшими в среднем более чем по одному критерию.
Для иллюстрации приведем простой пример оптимизации функций одной переменной относительно двух целевых функций [2,5]:
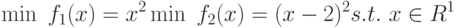
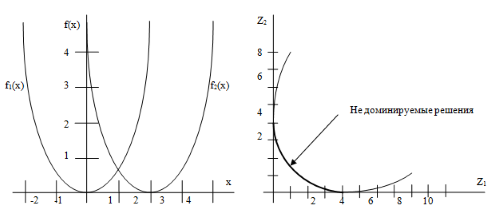
На рис.5.3 а) представлены две целевые функции с областью определения [-2,4]. Очевидно, что оптимальные по Парето решения попадают в [0,2]. На рис.5.3 б) этот пример представлен в пространстве критериев.
Для решения этой задачи использовался ГА с векторной оценкой [5] со следующими параметрами: мощность популяции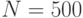 
, длина стринга 
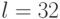, максимальное число поколений 
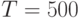, вероятности кроссинговера 
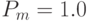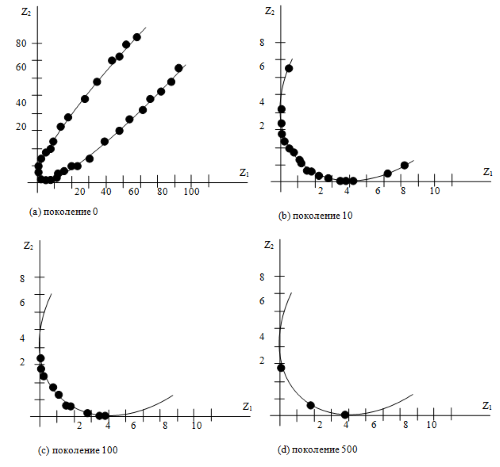
и мутации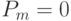 
. Начальная популяция генерировалась на отрезке [-10,10] в пространстве решений и показана на рис.5.4 а).
Из рис.5.4 b) видно, что при 
популяция начинает сходиться к недоминируемой области. Далее при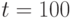 
популяция, в основном, концентрируется в недоминируемой области, что хорошо видно рис.5.4 с). Наконец, при 
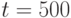популяция сходится только к трем решениям, как показано на рис.5.4 d). Это явление получило название видообразования.