Модификации генетических алгоритмов
3.1. Создание исходной популяции
В настоящее время наиболее известными и часто применяемыми на практике являются три способа создания исходной популяции (начального множества решений)[1,2].
Стратегия "одеяла" – формирование полной популяции, содержащей все возможные решения. Например, для  -разрядной хромосомы мы имеем всего
-разрядной хромосомы мы имеем всего  вариантов решений, которые составляют полную популяцию.
вариантов решений, которые составляют полную популяцию.
Стратегия "дробовика" - генерация достаточно большого случайного подмножества решений.
Стратегия фокусировки - генерация подмножества решений, включающих разновидности одного решения.
Первый подход (стратегия "одеяла") практически не реализуем даже для задач средней размерности, вследствие больших вычислительных затрат. Заметим, что при этом подходе начальная популяция не может развиваться, т.к. в ней уже содержатся все возможные решения.
Третий способ используется тогда, когда есть предположение, что некоторое решение является вариацией известного значения. В этом случае время поиска оптимального решения существенно сокращается, т.к. алгоритм начинает работу в окрестности оптимума.
Чаще всего применяют второй способ. В этом случае в результате эволюции есть возможность перейти в другие подобласти поиска и каждая из них имеет сравнительно небольшое пространство поиска.
В целом эффективность ГА, качество решения и дальнейшая эволюция в значительной степени определяются структурой и качеством начальной популяции.
На практике часто применяют комбинацию второго и третьего способов. Сначала определяются особи с высокими значениями целевой функции, а затем случайно формируются начальные решения в этих подобластях.
3.2. Отбор родителей (селекция)
Оператор отбора  порождает промежуточную популяцию
порождает промежуточную популяцию 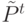 из текущей популяции
из текущей популяции 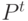 путем отбора и генерации новых копий особей:
путем отбора и генерации новых копий особей: 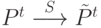 .
.
При отборе конкурентоспособных особей используют целевую (fitness) функцию, как единственно доступный источник информации о качестве решения. Но различные методы отбора родителей по-разному используют эту информацию. Далее мы рассмотрим наиболее распространенные методы отбора родителей [1,2,3].
3.2.1. Пропорциональный отбор (метод "рулетки")
Данный вид отбора чаще всего используется на практике. При этом особи (решения) отображаются в отрезки линии (или сектора рулетки) таким образом, что их размер пропорционален значению целевой функции для данной особи. Это показано в следующем примере, представленном в табл.3.1
| Номер особи | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Значение ЦФ | 2,0 | 1,8 | 1,6 | 1,4 | 1,2 | 1,0 | 0,8 | 0,6 | 0,4 | 0,2 | 0,0 |
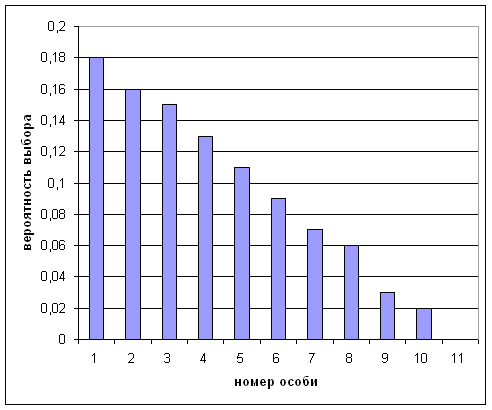
| Вероятность выбора | 0,18 | 0,16 | 0,15 | 0,13 | 0,11 | 0,09 | 0,07 | 0,06 | 0,03 | 0,02 | 0,0 |
Здесь на отрезке [0,1] для каждой особи строятся отрезки, длины которых пропорциональны вероятностям выбора особей, как это показано на рис.3.1
Далее случайно генерируются числа из диапазона [0,1] и в промежуточную популяцию выбираются те особи, в чей "отрезок" попадают эти случайные числа. Таким образом, каждая попытка представляет собой случайное число из отрезка [0,1], в результате чего выбирается особь, соответствующая выбранному отрезку. В данном примере в результате пяти попыток были выбраны в промежуточную популяцию особи 1, 2, 3, 6 и 9.
Данный метод, несмотря на частое применение, имеет следующие недостатки:
- зависимость от положительных значений целевой функции (функция должна для всех особей принимать положительное значение);
- метод может использоваться (без модификации) только в задачах максимизации (но не минимизации) функции;
- простое добавление очень большой константы к целевой функции может свести способ отбора практически к случайному выбору;
- особи с очень маленькими значениями фитнесс-функции слишком быстро исключаются из популяции, что может привести к преждевременной сходимости ГА.
Для устранения этих недостатков используют масштабирование оценок значений целевой функции относительно минимального значения в популяции (см. раздел 3.2.8) или метод ранжирования (раздел 3.2.2).
Очевидно, что проблема минимизации может быть сведена к задаче максимизации функции и обратно. Поэтому в некоторых реализациях ГА метод рулетки применяется и для поиска минимума функции, что в практических задачах встречается чаще (минимизация затрат, расстояния, погрешности и т.д.).
Для приведенного примера можно привести следующую гистограмму вероятностей выбора особей, представленную на рис.3.2. Отметим, что здесь высота "ступенек" различна, в отличие от следующего метода выбора, для которого гистограмма представлена на рис.3.3.
3.2.2. Ранжирование
При этом методе особи популяции сортируются (упорядочиваются) согласно значениям целевой функции. Отметим, что здесь вероятность отбора для каждой особи зависит только от ее позиции (номера) в этом упорядоченном множестве особей, а не от самого значения целевой функции. Этот метод отбора более устойчив, чем предыдущий. В основном применяют линейное ранжирование, где вероятность отбора особи определяют в соответствии со следующим выражением:
 |
( 3.1) |
- где
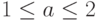 выбирается случайным образом;
выбирается случайным образом; -
 ;
; -
 – мощность популяции;
– мощность популяции; -
 – номер особи в упорядоченном списке.
– номер особи в упорядоченном списке.
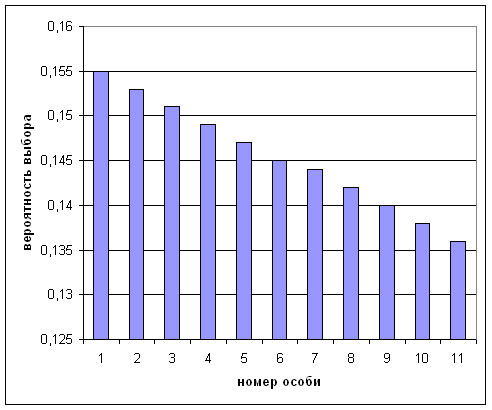
Для приведенного примера гистограмма вероятностей выбора особей методом ранжирования, представлена на рис.3.3. Отметим, что здесь высота "ступенек" (разность значений вероятностей отбора- высот столбцов) одинакова, в отличие от предыдущего метода выбора. Иногда применяют нелинейное ранжирование. При этом вероятность отбора также определяется номером позиции в упорядоченном множестве особей, но вид функции может быть сложнее.
Достоинством метода ранжирования является возможность его применения при поиске как максимумов, так и минимумов функций. Этот метод также не требует масштабирования для предотвращения преждевременной сходимости в отличие от метода рулетки.