|
Здравствуйте Владимир (Ефименко). Я обучаюсь по программе повышения квалификации "Наноэлектронная элементная база информатики на основе полупроводников и ферромагнетиков". У меня проблема с тестом № 2 (к лекции № 2) по этой программе. Я несколько раз пытался пройти этот тест, но больше 50 баллов набрать не удаётся, хотя я всё делаю в соответствии сматериалом лекции. В заданиях этого теста есть ошибки, которые видны невооружённым глазом. Обращаюсь к Вам как к инспектору этой программы повышения квалификации. Найдите возможность исправить ошибки в тесте № 2. Из-за остановки на этом тесте я не могу двигаться дальше, а у меня очень ограниченное время на освоение этой программы. Заранее благодарен Вам за внимание к моим проблемам и помощь. |
Одноэлектроника – одна из новых концепций построения НЭБИ
Одноэлектронные клеточные автоматы
Совсем другую концепцию эффективной обработки информации представляют собой т.н. "клеточные автоматы" (англ. Cellular Automata). Клеточные автоматы (термин употребляется только во множественном числе) – это логическая сеть, состоящая из одинаковых элементов. Каждый элемент такой сети (элементарный автомат, ячейка, отдельная "клетка" сети) может находиться в одном из нескольких дискретных состояний и переходить в другие состояния в зависимости от состояния соседних элементов. Уже давно математически доказано, что клеточные автоматы представляют собой функционально полную систему элементов и теоретически могут обеспечить обработку любой информации, которая может обрабатываться на универсальных ЭВМ.
Структура простейшего двоичного элемента для такой сети, построенного из 5 наноостровков проводника в диэлектрике, показана на
рис.
4.8.а. С помощью одноэлектронного туннелирования в такой элемент заводят 2 избыточных электрона ( ). Туннельные барьеры между центральным наноостровком
). Туннельные барьеры между центральным наноостровком 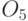 и каждым из наноостровков
и каждым из наноостровков 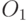 ,
, 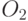 ,
, 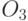 и
и 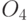 являются относительно прозрачными, так что электроны могут относительно легко мигрировать через центральный наноостровок на любой другой.
являются относительно прозрачными, так что электроны могут относительно легко мигрировать через центральный наноостровок на любой другой.
Согласно закону Кулона одноименно электрически заряженные электроны взаимно отталкиваются и поэтому стремятся занять места на противоположных наноостровках. Возможны 2 варианта устойчивого расположения двух электронов: на островках 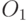 и
и 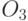 или на островках
или на островках 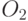 и
и 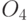 . Следовательно, в сети таких клеточных автоматов каждый элемент может находиться лишь в одном из двух состояний, одно из которых рассматривают как логический "0", а другое – как логическую "1" (
рис.
4.8.б).
. Следовательно, в сети таких клеточных автоматов каждый элемент может находиться лишь в одном из двух состояний, одно из которых рассматривают как логический "0", а другое – как логическую "1" (
рис.
4.8.б).
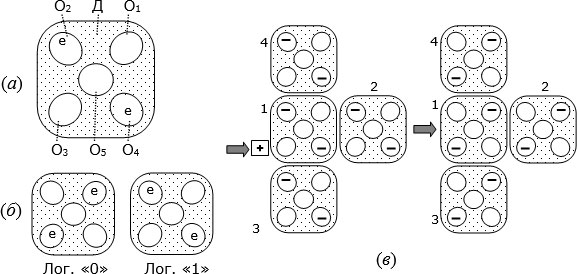
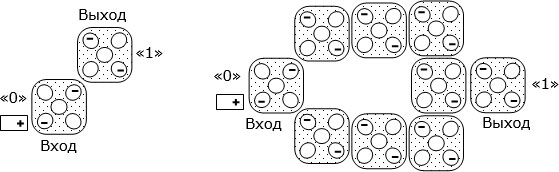
Рис. 4.8. а) Структура элемента сети одноэлектронных клеточных автоматов; б) кодирование состояний; в) самоорганизация состояний сети элементов при изменении состояния одного из них
Если разместить рядом несколько таких элементов так, чтобы они могли электрически взаимодействовать между собой, то силы кулоновского отталкивания электронов приводят к самоорганизации состояний этих элементов так, чтобы электроны расположились как можно дальше друг от друга. (При этом достигается минимум потенциальной энергии кулоновского взаимодействия).
На рис. 4.8.в слева показан пример рядом расположенных четырех одинаковых двоичных элементов сети. Сначала все они находятся в состояниях логической "1". Потом элемент 1 с помощью внешнего электрического поля (оно условно изображено квадратом с пометкой положительного потенциала "+") принудительно переводят в состояние логического "0". Тогда под действием кулоновских сил все другие элементы сети тоже переходят в состояние логического "0". Переход этот условно обозначен стрелкой. Справа показано результирующее состояние сети.
Если образовать из таких элементов "дорожку" ( рис. 4.9.а), то все они будут находиться в одинаковом состоянии, например, логического "0". Но если первый из них (Вход) с помощью внешнего электрического поля принудительно перевести в состояние логической "1", то и все другие элементы под действием кулоновских сил быстро перейдут в состояние логической "1" ( рис. 4.9.б). Вдоль дорожки почти мгновенно пробегает волна "переполяризации" элементов. И на противоположном конце дорожки (Выход) можно зарегистрировать изменение состояния (например, с помощью расположенного рядом с выходом одноэлектронного транзистора).

Рис. 4.9. Линия передачи информации через последовательность одноэлектронных клеточных автоматов: а) пример исходного состояния; б) состояние линии после изменения состояния входного элемента
При этом ни электрический заряд, ни энергия вдоль "дорожки" не переносятся. Передается лишь информация – почти мгновенно и с очень незначительными затратами энергии. Возможность передачи данных через такие "линии связи" значительно уменьшает потребность в системе многослойных металлических "разводок", характерных для современных полупроводниковых больших интегральных схем.
На рис. 4.10.а показана конфигурация одноэлектронных клеточных автоматов, которая функционирует как мажоритарный логический элемент. На ее выходе реализуется то логическое состояние, которое соответствует большинству состояний на входе.
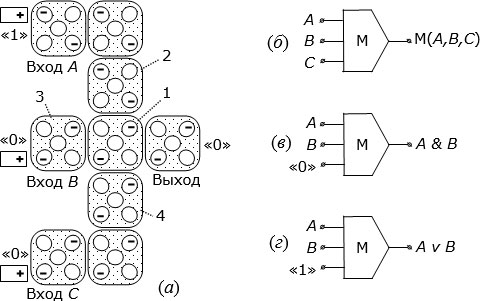
Рис. 4.10. а) Топология мажоритарного логического элемента из сети одноэлектронных клеточных автоматов; б) его обозначение в схемах; в) принцип реализации конъюнкции; г) принцип реализации дизъюнкции
Здесь показан случай, когда на входе  установлено состояние логической "1", а на входах
установлено состояние логической "1", а на входах  и
и  – состояние логического "0". На "ключевой" элементарный автомат 1 со стороны элементарного автомата 2 действуют кулоновские силы, побуждающие его перейти тоже в состояние логической "1". Но со стороны элементарных автоматов 3 и 4 действуют кулоновские силы, побуждающие его перейти в состояние логического "0". И поскольку их больше, то всей сети в целом энергетически выгоднее перейти в состояние логического "0". В результате на выходе формируется состояние логического "0".
Условное изображение такой логической схемы показано на
рис.
4.10.б. С помощью схемы мажоритарного логического элемента легко реализовать логические операции конъюнкции и дизъюнкции (
рис.
4.10.в,г). Мажоритарные логические элементы довольно перспективны также для построения и имитирования работы нейронных сетей.
– состояние логического "0". На "ключевой" элементарный автомат 1 со стороны элементарного автомата 2 действуют кулоновские силы, побуждающие его перейти тоже в состояние логической "1". Но со стороны элементарных автоматов 3 и 4 действуют кулоновские силы, побуждающие его перейти в состояние логического "0". И поскольку их больше, то всей сети в целом энергетически выгоднее перейти в состояние логического "0". В результате на выходе формируется состояние логического "0".
Условное изображение такой логической схемы показано на
рис.
4.10.б. С помощью схемы мажоритарного логического элемента легко реализовать логические операции конъюнкции и дизъюнкции (
рис.
4.10.в,г). Мажоритарные логические элементы довольно перспективны также для построения и имитирования работы нейронных сетей.
Два возможных варианта реализации логического отрицания с помощью клеточных автоматов показаны на рис. 4.11: слева – простейший вариант, справа – более сложный, но и более надежный в работе и допускающий разветвление.
На основе одноэлектронных клеточных автоматов можно строить довольно сложные логические схемы и процессоры для цифровой обработки сигналов. Подсчитано, например, что при размерах наноостровков 20х20 нм один разряд многоразрядного сумматора с переносами, сформированного из одноэлектронных клеточных автоматов, можно разместить на площади приблизительно 1,5 мкм2. Такую приблизительно площадь занимает обычно лишь один КМДП транзистор в современных интегральных схемах.
Скорость работы такого сумматора может достигать нескольких квадриллионов операций/с при очень низком энергопотреблении – порядка 10-10 Вт/бит. В таких схемах не нужны многослойные металлические межсоединения. Ведь разветвление логических сигналов, их передача и объединение легко реализуются с помощью дорожек из таких самых одноэлектронных клеточных автоматов.
В завершение данного пункта сделаем важные замечания относительно употребляемой терминологии. В литературе металлические наноостровки в одноэлектронных схемах (все вместе, несмотря на их размеры) часто называют "квантовыми точками". Но при размерах порядка 10 нм и более это далеко не всегда верно. Как мы уже показали в лекции 3, в квантовых точках энергетические состояния электронов квантованы, в то время как в металлических наноостровках размером свыше 10 нм такое квантование еще не наблюдается, и поведение электронов можно описывать в терминах классической физики. В таких случаях точнее употреблять именно термин "наноостровок" и некорректно употреблять термин "квантовая точка". От некорректно употребляемого термина "квантовая точка" пошли названия "квантовые клеточные автоматы", "клеточные автоматы на квантовых точках" или "квантово-точечные клеточные автоматы" (англ. "quantum cellular automata", "QCA" и соответственно "quantum dot cellular automation", "QDCA"). Для описанных выше одноэлектронных клеточных автоматов такие названия не подходят.
Если размеры наноостровков становятся настолько малыми, что они и впрямь превращаются в "квантовые точки", то показанную на
рис.
4.8.а структуру уже никак нельзя рассматривать как классическую, а надо рассматривать как квантовую и описывать волновыми функциями. По законам квантовой механики такая структура может находиться не только в базовых состояниях "0" и "1", но и во многих других "смешанных" состояниях. Ее уже нельзя рассматривать как классический "бит", а надо рассматривать как "кубит".
Подробнее об этом мы расскажем вам в цикле лекций "Наноэлектронная элементная база информатики. Качественно новые направления". Именно для таких одноэлектронных клеточных автоматов, функционирующих уже по принципам квантовой механики, и надо применять названия "квантовые клеточные автоматы" или "квантово-точечные клеточные автоматы" ( . "quantum cellular automata", "QCA" и соответственно "quantum dot cellular automation", "QDCA"). Здесь же мы рассмотрели лишь "классические" одноэлектронные клеточные автоматы.
. "quantum cellular automata", "QCA" и соответственно "quantum dot cellular automation", "QDCA"). Здесь же мы рассмотрели лишь "классические" одноэлектронные клеточные автоматы.