Генерация кода

Генерация оптимального кода методами синтаксического анализа

Сопоставление образцов

Техника генерации кода, рассмотренная выше, основывалась на однозначном соответствии структуры промежуточного представления и описывающей это представление грамматики. Недостатком такого "жесткого" подхода является то, что как правило одну и ту же программу на промежуточном языке можно реализовать многими различными способами в системе команд машины. Эти разные реализации могут иметь различную длину, время выполнения и другие характеристики. Для генерации более качественного кода может быть применен подход, изложенный в настоящей главе.

Этот подход основан на понятии "сопоставления образцов": командам машины сопоставляются некоторые "образцы", вхождения которых ищутся в промежуточном представлении программы, и делается попытка "покрыть" промежуточную программу такими образцами. Если это удается, то по образцам восстанавливается программа уже в кодах. Каждое такое покрытие соответствует некоторой программе, реализующей одно и то же промежуточное представление.

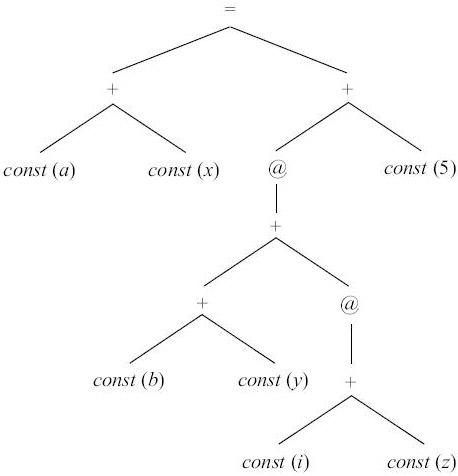
На рис. 9.24 показано промежуточное дерево для

Рис. 9.24.

оператора a = b[i] + 5, где a, b, i - локальные переменные, хранимые со смещениями x, y, z соответственно в областях данных с одноименными адресами.

Элемент массива b занимает память в одну машинную единицу. 0 -местная операция const возвращает значение атрибута соответствующей вершины промежуточного дерева, указанного на рисунке в скобках после оператора. Одноместная операция @ означает косвенную адресацию и возвращает содержимое регистра или ячейки памяти, имеющей адрес, задаваемый аргументом операции.

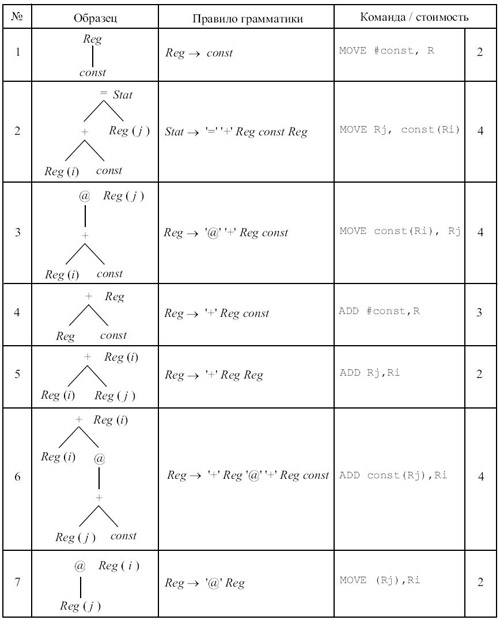
На рис. 9.25 показан пример сопоставления образцов машинным командам. Приведены два варианта задания образца: в виде дерева и в виде правила контекстно-свободной грамматики. Для каждого образца указана машинная команда, реализующая этот образец, и стоимость этой команды.

В каждом дереве-образце корень или лист может быть

Рис. 9.25.

помечен терминальным и/или нетерминальным символом. Внутренние вершины помечены терминальными символами - знаками операций. При наложении образца на дерево выражения, во-первых, терминальный символ образца должен соответствовать терминальному символу дерева, и, во-вторых, образцы должны "склеиваться" по типу нетерминального символа, то есть тип корня образца должен совпадать с типом вершины, в которую образец подставляется корнем. Допускается использование "цепных" образцов, то есть образцов, корню которых не соответствует терминальный символ, и имеющих единственный элемент в правой части. Цепные правила служат для приведения вершин к одному типу. Например, в рассматриваемой системе команд одни и те же регистры используются как для целей адресации, так и для вычислений. Если бы в системе команд для этих целей использовались разные группы регистров, то в грамматике команд могли бы использоваться разные нетерминалы, а для пересылки из адресного регистра в регистр данных могла бы использоваться соответствующая команда и образец.

Нетерминалы Reg на образцах могут быть помечены индексом ( i или j ), что (неформально) соответствует номеру регистра и служит лишь для пояснения смысла использования регистров. Отметим, что при генерации кода рассматриваемым методом не осуществляется распределение регистров. Это является отдельной задачей. Стоимость может определяться различными способами, например числом обращений к памяти при выборке и исполнении команды. Здесь мы не рассматриваем этого вопроса. На рис. 9.26 приведен пример покрытия промежуточного дерева рис. 9.24 образцами рис. 9.25. В рамки заключены фрагменты дерева, сопоставленные образцу правила, номер которого указывается в левом верхнем углу рамки. В квадратных скобках указаны результирующие вершины.

Приведенное покрытие дает такую последовательность команд:

1 MOVE #b,Rb
4 ADD #y,Rb
1 MOVE #i,Ri
6 ADD #z(Ri),Rb
7 MOVE (Rb),Rb
4 ADD #5,Rb

1 MOVE #a,Ra

Рис. 9.26.

2 MOVE Rb,#x(Ra)

Основная идея подхода заключается в том, что каждая команда машины описывается в виде такого образца. Различные покрытия дерева промежуточного представления соответствуют различным последовательностям машинных команд. Задача выбора команд состоит в том, чтобы выбрать наилучший способ реализации того или иного действия или последовательности действий, то есть выбрать в некотором смысле оптимальное покрытие.

Для выбора оптимального покрытия было предложено несколько интересных алгоритмов, в частности использующих динамическое программирование [ 14, 16 ]. Мы здесь рассмотрим алгоритм [ 15 ], комбинирующий возможности синтаксического анализа и динамического программирования. В основу этого алгоритма положен синтаксический анализ неоднозначных грамматик (модифицированный алгоритм Кока, Янгера и Касами [ 18, 19 ]), эффективный в реальных приложениях. Этот же метод может быть применен и тогда, когда в качестве промежуточного представления используется дерево.

Синтаксический анализ для T-грам- матик

Обычно код генерируется из некоторого промежуточного языка с довольно жесткой структурой. В частности, для каждой операции известна ее размерность, то есть число операндов, большее или равное 0. Операции задаются терминальными символами, и наоборот - будем считать все терминальные символы знаками операций. Назовем грамматики, удовлетворяющие этим ограничениям, T -грам- матиками. Правая часть каждой продукции в Т -грамматике есть правильное префиксное выражение, которое может быть задано следующим определением:

1. Операция размерности 0 является правильным префиксным выражением;
2. Нетерминал является правильным префиксным выражением;
3. Префиксное выражение, начинающееся со знака операции размерности n > 0, является правильным, если после знака операции следует n правильных префиксных выражений;
4. Ничто другое не является правильным префиксным выражением

Образцы, соответствующие машинным командам, задаются правилами грамматики (вообще говоря, неоднозначной). Генератор кода анализирует входное префиксное выражение и строит одновременно все возможные деревья разбора. После окончания разбора выбирается дерево с наименьшей стоимостью. Затем по этому единственному оптимальному дереву генерируется код.

Для T -грамматик все цепочки, выводимые из любого нетерминала A, являются префиксными выражениями с фиксированной арностью операций. Длины всех выражений из входной цепочки a₁ ... a_n можно предварительно вычислить (под длиной выражения имеется ввиду длина подстроки, начинающейся с символа кода операции и заканчивающейся последним символом, входящим в выражение для этой операции). Поэтому можно проверить, сопоставимо ли некоторое правило с подцепочкой ai : : : ak входной цепочки a₁ ... a_n, проходя слева-направо по a_i ... a_k. В процессе прохода по цепочке предварительно вычисленные длины префиксных выражений используются для того, чтобы перейти от одного терминала к следующему терминалу, пропуская подцепочки, соответствующие нетерминалам правой части правила.

Цепные правила не зависят от операций, следовательно, их необходимо проверять отдельно. Применение одного цепного правила может зависеть от применения другого цепного правила. Следовательно, применение цепных правил необходимо проверять до тех пор, пока нельзя применить ни одно из цепных правил. Мы предполагаем, что в грамматике нет циклов в применении цепных правил. Построение всех вариантов анализа для T-грамматики дано ниже в алгоритме 9.5. Тип Titem в алгоритме 9.5 ниже служит для описания ситуаций (то есть правил вывода и позиции внутри правила). Тип Tterminal - это тип терминального символа грамматики, тип Tproduction - тип для правила вывода.

Tterminal a[n];
setofTproduction r[n];
int l[n]; // l[i] - длина a[i]-выражения
Titem h; // используется при поиске правил,
	// сопоставимых с текущей подцепочкой
	
// Предварительные вычисления
Для каждой позиции i вычислить длину
	a[i]-выражения l[i];
// Распознавание входной цепочки
 for (int i=n-1;i>=0;i--){
  for (каждого правила A -> a[i] y из P){
   j=i+1;
   if (l[i]>1)
   // Первый терминал a[i] уже успешно
   // сопоставлен
    {h=[A->a[i].y];
    do
     // найти a[i]y, сопоставимое
     // с a[i]..a[i+l[i]-1]
     {Пусть h==[A->u.Xv];
      if (X in T)
       if (X==a[j]) j=j+1; else break;
      else // X in N
       if (имеется X->w in r[j]) j=j+l[j];
       else break;
      h=[A->uX.v];
      //перейти к следующему символу
  }
    while (j!=i+l[i]);
   } // l[i]>1
  if (j==i+l[i]) r[i]=r[i] + { (A->a[i]y) }
} // for по правилам A -> a[i] y
// Сопоставить цепные правила
while (существует правило C->A из P такое, что
	имеется некоторый элемент (A->w) в r[i]
	и нет элемента (C->A) в r[i])
	r[i]=r[i] + { (C->A) };
} // for по i

Проверить, принадлежит ли (S->w) множеству r[0] ; Множества r[i] имеют размер O(|P|). Можно показать, что алгоритм имеет временную и емкостную сложность O(n). Рассмотрим вновь пример рис. 9.24. В префиксной записи приведенный фрагмент программы записывается следующим образом:

= + a x + @ + + b y @ + i z 5

На рис. 9.27 приведен результат работы алгоритма. Правила вычисления стоимости приведены в следующем разделе. Все возможные выводы входной цепочки (включая оптимальный) можно построить, используя таблицу l длин префиксных выражений и таблицу r применимых правил. Операция Длина Правила (стоимость)

Рис. 9.27.