Генерация кода

Пусть G - это T -грамматика. Для каждой цепочки z из L(G) можно построить абстрактное синтаксическое дерево соответствующего выражения ( рис. 9.24). Мы можем переписать алгоритм так, чтобы он принимал на входе абстрактное синтаксическое дерево выражения, а не цепочку. Этот вариант алгоритма приведен ниже. В этом алгоритме дерево выражения обходится сверху вниз и в нем ищутся поддеревья, сопоставимые с правыми частями правил из G. Обход дерева осуществляется процедурой PARSE. После обхода поддерева данной вершины в ней применяется процедура MATCHED, которая пытается найти все образцы, сопоставимые поддереву данной вершины. Для этого каждое правило-образец разбивается на компоненты в соответствии с встречающимися в нем операциями. Дерево обходится справа налево только для того, чтобы иметь соответствие с порядком вычисления в алгоритме 9.5. Очевидно, что можно обходить дерево вывода и слева направо.

Структура данных, представляющая вершину дерева, имеет следующую форму:

struct Tnode {
  Tterminal op;
  Tnode * son[MaxArity];
  setofTproduction RULEs;
};

В комментариях указаны соответствующие фрагменты алгоритма 9.5.

Tnode * root;

bool MATCHED(Tnode * n, Titem h)
 { bool matching;
  пусть h==Xv, v== v"1 v"2 ... v"m, m=Arity(X);
   if (X in T)// сопоставление правила
    if (m==0) // if l[i]==1
      if (X==n->op) //if X==a[j]
       return(true);
    else
     return(false);
   else // if l[i]>1
    if (X==n->op) //if X==a[j]
     {matching=true;
      for (i=1;i<=m;i++) //j=j+l[j]
       matching=matching && // while (j==i+l[i])
        MATCHED(n->son[i-1],v"i);
       return(matching); //h=[A->uX.v]
      }
     else
       return(false);
    else // X in N поиск подвывода
      if (в n^.RULEs имеется правило
		с левой частью X)
       return(true);
    else
     return(false);
  }
void PARSE(Tnode * n)
 {
  for (i=Arity(n->op);i>=1;i--)
  // for (i=n; i>=1;i--)
    PARSE(n->son[i-1]);
  n->RULEs=EMPTY;
  for (каждого правила A->bu из P такого,
  		что b==n->op)
    if (MATCHED(n,bu)) // if (j==i+l[i])
     n->RULEs=n->RULEs+{(A->bu)};
  // Сопоставление цепных правил
   while (существует правило C->A из P такое, что
     	некоторый элемент (A->w) в n->RULEs
		и нет элемента (C->A) в n->RULEs)
	 n->RULEs=n->RULEs+{(C->A)};
   }
Основная программа
//Предварительные вычисления
Построить дерево выражения для входной цепочки z;
root = указатель дерева выражения;
//Распознать входную цепочку
PARSE(root);

Проверить, входит ли во множество root->RULEs
правило с левой частью S;

Выходом алгоритма является дерево выражения для z, вершинам которого сопоставлены применимые правила. С помощью такого дерева можно построить все выводы для исходного префиксного выражения.

Выбор дерева вывода наименьшей стоимости

T -грамматики, описывающие системы команд, обычно являются неоднозначными. Чтобы сгенерировать код для некоторой входной цепочки, необходимо выбрать одно из возможных деревьев вывода. Это дерево должно представлять желаемое качество кода, например размер кода и/или время выполнения.

Для выбора дерева из множества всех построенных деревьев вывода можно использовать атрибуты стоимости, атрибутные формулы, вычисляющие их значения, и критерии стоимости, которые оставляют для каждого нетерминала единственное применимое правило. Атрибуты стоимости сопоставляются всем нетерминалам, атрибутные формулы - всем правилам T -грамматики.

Предположим, что для вершины n обнаружено применимое правило

p : A -> z₀X₁z₁ ... X_kz_k;

где 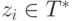для 0 <= i <= k и 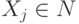для 0 <= j <= k . Вершина n имеет потомков n1; : : : ; nk, которые соответствуют нетерминалам X₁,..., X_k. Значения атрибутов стоимости вычисляются обходя дерево снизу вверх. Вначале атрибуты стоимости инициализируются неопределенным значением UndefinedValue. Предположим, что значения атрибутов стоимости для всех потомков n₁,..., n_k вершины n вычислены. Если правилу p сопоставлена формула

a(A) = f(b(X_i), c(X_j),...) для 1 <= i, j <= k ;

то производится вычисление значения атрибута a нетерминала A в вершине n. Для всех примененных правил ищется такое, которое дает минимальное значение стоимости. Отсутствие примененных правил обозначается через Undefined, значение которого полагается большим любого определенного значения.

Добавим в алгоритм 9.6 реализацию атрибутов стоимости, формул их вычисления и критериев отбора. Из алгоритма можно исключить поиск подвыводов, соответствующих правилам, для которых значение атрибута стоимости не определено. Структура данных, представляющая вершину дерева, принимает следующий вид:

struct Tnode {
	Tterminal op;
	Tnode * son[MaxArity];
	struct * { unsigned CostAttr;
		Tproduction Production;
		} nonterm [Tnonterminal];
OperatorAttributes ...
  Тело процедуры PARSE принимает вид
  void PARSE(Tnode *n)
{for (i=Arity(n->op);i>=1;i--)
	PARSE(n->son[i]);
	for (каждого A из N)
	{n->nonterm[A].CostAttr=UndefinedValue;
	 n->nonterm[A].production=Undefined; }
	for (каждого правила A->bu из P
	   такого, что b==n->op)
	 if (MATCHED(n,bu))
	  {ВычислитьАтрибутыСтоимостиДля(A,n,(A->bu));
	ПроверитьКритерийДля(A,
		n->nonterm[A].CostAttr);
	 if ((A->bu) лучше,
		чем ранее обработанное правило для A)
		{Модифицировать(n->nonterm[A].CostAttr);
		n->nonterm[A].production=(A->bu); }
	}
// Сопоставить цепные правила
while (существует правило C->A из P, которое
	лучше, чем ранее обработанное правило для A)
  {ВычислитьАтрибутыСтоимостиДля(C,n,(C->A));
   ПроверитьКритерийДля(C,n->nonterm[C].CostAttr);
   if ((C->A) лучше)
    {Модифицировать(n->nonterm[C].CostAttr);
	 n->nonterm[C].production=(C->A); }
  }
}

Процедура ВычислитьАтрибутыСтоимостиДля (A, n, (A -> bu)) вычисляет стоимость применения правила в данной вершине для данного нетерминала.

Процедура ПроверитьКритерийДля(C, n -> nonterm[C]: CostAttr) определяет наилучшее правило.

Процедура Модифицировать (n -> nonterm[C]:CostAttr) позволяет хранить это наилучшее значение в варианте. Дерево наименьшей стоимости определяется как дерево, соответствующее минимальной стоимости корня. Когда выбрано дерево вывода наименьшей стоимости, вычисляются значения атрибутов, сопоставленных вершинам дерева вывода, и генерируются соответствующие машинные команды. Вычисление значений атрибутов, генерация кода осуществляются в процессе обхода выбранного дерева вывода сверху вниз, слева направо. Обход выбранного дерева вывода выполняется процедурой вычислителя атрибутов, на вход которой поступают корень дерева выражения и аксиома грамматики. Процедура использует правило A -> z₀X₁z₁ ... X_kz_k, связанное с указанной вершиной n, и заданный нетерминал A, чтобы определить соответствующие им вершины n₁,..., n_k и нетерминалы X₁,..., X_k. Затем вычислитель рекурсивно обходит каждую вершину n_i, имея на входе нетерминал X_i.

Атрибутная схема для алгоритма сопоставления образцов

Алгоритмы 9.5 и 9.6 являются "универсальными" в том смысле, что конкретные грамматики выражений и образцов являются, по-существу, параметрами этих алгоритмов. В то же время, для каждой конкретной грамматики можно написать свой алгоритм поиска образцов. Например, в случае нашей грамматики выражений и приведенных на рис. 9.25 образцов алгоритм 9.6 может быть представлен атрибутной грамматикой, приведенной ниже.

Наследуемый атрибут Match содержит упорядоченный список (вектор) образцов для сопоставления в поддереве данной вершины. Каждый из образцов имеет вид либо <op op-list> (op - операция в данной вершине, а op- list - список ее операндов), либо представляет собой нетерминал N. В первом случае op-list "распределяется" по потомкам вершины для дальнейшего сопоставления. Во втором случае сопоставление считается успешным, если есть правило N -> op fPatig, где w состоит из образцов, успешно сопоставленных потомкам данной вершины. В этом случае по потомкам в качестве образцов распределяются элементы правой части правила. Эти два множества образцов могут пересекаться. Синтезируемый атрибут Pattern - вектор логических значений, дает результат сопоставления по вектору-образцу Match.

Таким образом, при сопоставлении образцов могут встретиться два случая:

1. Вектор образцов содержит образец <op fPatig>, где op - операция, примененная в данной вершине. Тогда распределяем образцы Pati по потомкам и сопоставление по данному образцу считаем успешным (истинным), если успешны сопоставления элементов этого образца по всем потомкам.
2. Образцом является нетерминал N. Тогда рассматриваем все правила вида N -> op fPatig. Вновь распределяем образцы Pati по потомкам и сопоставление считаем успешным (истинным), если успешны сопоставления по всем потомкам. В общем случае успешным может быть сопоставление по нескольким образцам.

Отметим, что в общем случае в потомки одновременно передается неско-лько образцов для сопоставления. В приведенной ниже атрибутной схеме не рассматриваются правила выбора покрытия наименьшей стоимости (см. предыдущий раздел). Выбор оптимального покрытия может быть сделан еще одним проходом по дереву, аналогично тому, как это было сделано выше. Например, в правиле с '+' имеется несколько образцов для Reg, но реального выбора одного из них не осуществляется. Кроме того, не уточнены некоторые детали реализации. В частности, конкретный способ формирования векторов Match и Pattern. В тексте употребляется термин "добавить", что означает добавление к вектору образцов очередного элемента. Векторы образцов записаны в угловых скобках.

RULE
Stat ::= '=' Reg Reg
SEMANTICS
Match<2>=<'+' Reg Const>;
Match<3>=<Reg>;
Pattern<0>[1]=Pattern<2>[1]&Pattern<3>[1].

Этому правилу соответствует один образец 2. Поэтому в качестве образцов потомков через их атрибуты Match передаются, соответственно, <'+' Reg Const> и <Reg>.

RULE
Reg ::= '+' Reg Reg
SEMANTICS
if (Match<0> содержит Reg в позиции i)
 {Match<2>=<Reg,Reg,Reg>;
  Match<3>=<Const,Reg,<'@' '+' Reg       Const>>;
  }
if (Match<0> содержит образец <'+' Reg Const>
в позиции j)
  {добавить Reg к Match<2> в некоторой позиции k;
  добавить Const к Match<3> в некоторой позиции k;
  }
if (Match<0> содержит образец <'+' Reg Const>
		в позиции j)
Pattern<0>[j]=Pattern<2>[k]&Pattern<3>[k];
if (Match[0] содержит Reg в i-й позиции)
Pattern<0>[i]=(Pattern<2>[1]&Pattern<3>[1])
		|(Pattern<2>[2]&Pattern<3>[2])
		|(Pattern<2>[3]&Pattern<3>[3]).

Образцы, соответствующие этому правилу, следующие:

(4) Reg -> '+' Reg Const,
(5) Reg -> '+' Reg Reg,
(6) Reg -> '+' Reg '@' '+' Reg Const.

Атрибутам Match второго и третьего символов в качестве образцов при сопоставлении могут быть переданы векторы <Reg, Reg, Reg> и <Const, Reg, <'@' '+' Reg Const>>, соответственно. Из анализа других правил можно заключить, что при сопоставлении образцов предков левой части данного правила атрибуту Match символа левой части может быть передан образец <'+' Reg Const> (из образцов 2, 3, 6) или образец Reg.

RULE
Reg ::= '@' Reg
SEMANTICS
 if (Match<0> содержит Reg в i-й позиции)
  Match<2>=<<'+' Reg Const>,Reg>;
   if (Match<0> содержит <'@' '+' Reg   Const>
    в j-й позиции)
   добавить к Match<2> <'+' Reg Const> в k позиции;
  if (Match<0> содержит Reg в i-й позиции)

Pattern<0>[i]=Pattern<2>[1]|Pattern<2>[2];
if (Match<0> содержит <'@' '+' Reg Const>
в j-й позиции)
  Pattern<0>[j]=Pattern<2>[k].

Образцы, соответствующие этому правилу, следующие:

(3) Reg -> '@' '+' Reg Const,
(7) Reg -> '@' Reg.

Соответственно, атрибуту Match второго символа в качестве образцов при сопоставлении могут быть переданы <'+' Reg Const> (образец 3) или <Reg> (образец 7). Из анализа других правил можно заключить, что при сопоставлении образцов предков левой части данного правила атрибуту Match могут быть переданы образцы <'@' '+' Reg Const> (из образца 6) и Reg.

RULE
Reg ::= Const
SEMANTICS
if (Pattern<0> содержит Const в j-й позиции)
Pattern<0>[j]=true;
if (Pattern<0> содержит Reg в i-й позиции)
Pattern<0>[i]=true.

Для дерева рис. 9.24 получим значения атрибутов, приведенные на рис. 9.28. Здесь M обозначает Match, P - Pattern, C - Const, R - Reg.

Рис. 9.28.