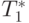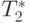Параллельные методы на графах
10.2.5. Анализ эффективности параллельных вычислений
Общий анализ сложности параллельного алгоритма Прима для нахождения минимального охватывающего дерева дает идеальные показатели эффективности параллельных вычислений:
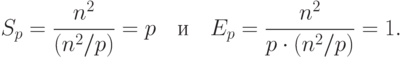 |
( 10.4) |
При этом следует отметить, что в ходе параллельных вычислений идеальная балансировка вычислительной нагрузки процессоров может быть нарушена. В зависимости от вида исходного графа G количество выбранных вершин в охватывающем дереве на разных процессорах может оказаться различным, и распределение вычислений между процессорами станет неравномерным (вплоть до отсутствия вычислительной нагрузки на отдельных процессорах). Однако такие предельные ситуации нарушения балансировки в общем случае возникают достаточно редко, а организация динамического перераспределения вычислительной нагрузки между процессорами в ходе вычислений является интересной, но одновременно и очень сложной задачей.
Для уточнения полученных показателей эффективности параллельных вычислений оценим более точно количество вычислительных операций алгоритма и учтем затраты на выполнение операций передачи данных между процессорами.
При выполнении вычислений на отдельной итерации параллельного алгоритма Прима каждый процессор определяет номер ближайшей
вершины из Vj до охватывающего дерева и осуществляет
корректировку расстояний di после расширения МОД. Количество
выполняемых операций в каждой из этих вычислительных процедур
ограничивается сверху числом вершин, имеющихся на процессорах, т.е.
величиной 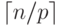 . Как результат, с учетом общего количества
итераций n время выполнения вычислительных операций параллельного алгоритма Прима может быть оценено при помощи соотношения:
. Как результат, с учетом общего количества
итераций n время выполнения вычислительных операций параллельного алгоритма Прима может быть оценено при помощи соотношения:
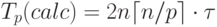 |
( 10.5) |
 есть время выполнения одной элементарной скалярной операции).
есть время выполнения одной элементарной скалярной операции).Операция сбора данных от всех процессоров на одном из
процессоров может быть произведена за 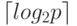 итераций, при этом
общая оценка длительности выполнения передачи данных определяется
выражением (более подробное рассмотрение данной коммуникационной
операции содержится в
"Оценка коммуникационной трудоемкости параллельных алгоритмов"
):
итераций, при этом
общая оценка длительности выполнения передачи данных определяется
выражением (более подробное рассмотрение данной коммуникационной
операции содержится в
"Оценка коммуникационной трудоемкости параллельных алгоритмов"
):
 |
( 10.6) |
 – латентность сети передачи данных,
– латентность сети передачи данных,  – пропускная
способность сети, а w есть размер одного пересылаемого элемента
данных в байтах (коэффициент 3 в выражении соответствует числу
передаваемых значений между процессорами – длина минимальной дуги
и номера двух вершин, которые соединяются этой дугой).
– пропускная
способность сети, а w есть размер одного пересылаемого элемента
данных в байтах (коэффициент 3 в выражении соответствует числу
передаваемых значений между процессорами – длина минимальной дуги
и номера двух вершин, которые соединяются этой дугой).Коммуникационная операция передачи данных от одного процессора
всем процессорам вычислительной системы также может быть
выполнена за 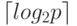 итераций при общей оценке времени выполнения
вида:
итераций при общей оценке времени выполнения
вида:
 |
( 10.7) |
С учетом всех полученных соотношений общее время выполнения параллельного алгоритма Прима составляет:
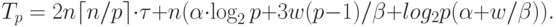 |
( 10.8) |
10.2.6. Результаты вычислительных экспериментов
Вычислительные эксперименты для оценки эффективности параллельного алгоритма Прима осуществлялись при тех же условиях, что и ранее выполненные (см. п. 10.1.7).
Для оценки длительности  базовой скалярной операции
проводилось решение задачи нахождения минимального охватывающего
дерева при помощи последовательного алгоритма и полученное таким
образом время вычислений делилось на общее количество выполненных
операций – в результате подобных экспериментов для величины
базовой скалярной операции
проводилось решение задачи нахождения минимального охватывающего
дерева при помощи последовательного алгоритма и полученное таким
образом время вычислений делилось на общее количество выполненных
операций – в результате подобных экспериментов для величины  было получено значение 4,76 нсек. Все вычисления производились
над числовыми значениями типа int, размер которого на данной
платформе равен 4 байта (следовательно, w=4 ).
было получено значение 4,76 нсек. Все вычисления производились
над числовыми значениями типа int, размер которого на данной
платформе равен 4 байта (следовательно, w=4 ).
Результаты вычислительных экспериментов даны в таблице 10.3. Эксперименты проводились с использованием двух, четырех и восьми процессоров. Время указано в секундах.
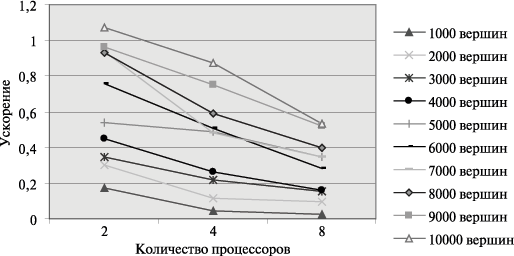
Рис. 10.7. Графики зависимости ускорения параллельного алгоритма Прима от числа используемых процессоров при различном количестве вершин в модели
Сравнение времени выполнения эксперимента 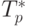 и теоретической
оценки Tp из (10.8) приведено в таблице 10.4 и на рис. 10.8.
и теоретической
оценки Tp из (10.8) приведено в таблице 10.4 и на рис. 10.8.
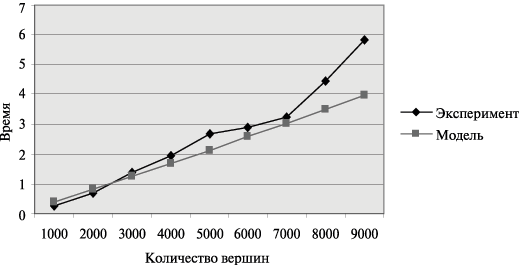
Рис. 10.8. Графики экспериментально установленного времени работы параллельного алгоритма Прима и теоретической оценки в зависимости от количества вершин в модели при использовании двух процессоров
Как можно заметить из табл. 10.4 и рис. 10.8, теоретические оценки определяют время выполнения алгоритма Прима с достаточно высокой погрешностью. Причина такого расхождения может состоять в том, что модель Хокни менее точна при оценке времени передачи сообщений с небольшим объемом передаваемых данных. Для уточнения получаемых оценок необходимым является использование других более точных моделей расчета трудоемкости коммуникационных операций – обсуждение этого вопроса проведено в "Оценка коммуникационной трудоемкости параллельных алгоритмов" .