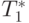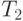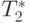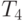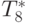Параллельные методы на графах

10.1.6. Программная реализация

Представим возможный вариант параллельной реализации алгоритма Флойда. При этом описание отдельных модулей не приводится, если их отсутствие не оказывает влияния на понимание общей схемы параллельных вычислений.

1. Главная функция программы. Реализует логику работы алгоритма, последовательно вызывает необходимые подпрограммы.

// Программа 10.1. — Алгоритм Флойда
int ProcRank;    // Ранг текущего процесса
int ProcNum;     // Количество процессов

// Функция вычисления минимума
int Min(int A, int B) {
  int Result = (A < B) ? A : B;

  if((A < 0) && (B >= 0)) Result = B;
  if((B < 0) && (A >= 0)) Result = A;
  if((A < 0) && (B < 0))  Result = -1;

  return Result;
}

// Главная функция программы
int main(int argc, char* argv[]) {
  int *pMatrix;     	// Матрица смежности
  int  Size;        	// Размер матрицы смежности
  int *pProcRows;   	// Строки матрицы смежности текущего процесса
  int  RowNum;      	// Число строк для текущего процесса

  MPI_Init(&argc, &argv);
  MPI_Comm_size(MPI_COMM_WORLD, &ProcNum);
  MPI_Comm_rank(MPI_COMM_WORLD, &ProcRank);

  // Инициализация данных
  ProcessInitialization(pMatrix, pProcRows, Size, RowNum);

  // Распределение данных между процессами
  DataDistribution(pMatrix, pProcRows, Size, RowNum);

  // Параллельный алгоритм Флойда
  ParallelFloyd(pProcRows, Size, RowNum);

  // Сбор результатов работы алгоритма
  ResultCollection(pMatrix, pProcRows, Size, RowNum);

  // Завершение вычислений процесса
  ProcessTermination(pMatrix, pProcRows);

  MPI_Finalize();
  return 0;
}

Функция Min вычисляет меньшее из двух целых чисел, учитывая применяемый способ задания несуществующих дуг в матрице смежности (в рассматриваемой реализации для этого используется значение -1).

Функция ProcessInitialization определяет исходные данные решаемой задачи (количество вершин графа ), выделяет память для хранения данных, осуществляет ввод матрицы смежности (или формирует ее при помощи какого-либо датчика случайных числе).

Функция DataDistribution распределяет исходные данные между процессами. Каждый процесс получает горизонтальную полосу матрицы смежности.

Функция ResultCollection осуществляет сбор со всех процессов горизонтальных полос результирующей матрицы кратчайших расстояний между любыми парами вершин графа.

Функция ProcessTermination выполняет необходимый вывод результатов решения задачи и освобождает всю ранее выделенную память для хранения данных.

Реализация всех перечисленных функций может быть выполнена по аналогии с ранее рассмотренными примерами и предоставляется читателю в качестве самостоятельного упражнения.

2. Функция ParallelFloyd. Данная функция осуществляет итеративное изменение матрицы смежности в соответствии с алгоритмом Флойда.

// Параллельный алгоритм Флойда
void ParallelFloyd(int *pProcRows, int Size, int RowNum) {
  int *pRow = new int[Size];
  int t1, t2;

  for(int k = 0; k < Size; k++) {
    // Распределение k-й строки среди процессов 
    RowDistribution(pProcRows, Size, RowNum, k, pRow);

    // Обновление элементов матрицы смежности
    for(int i = 0; i < RowNum; i++) 
      for(int j = 0; j < Size; j++)
        if( (pProcRows[i * Size + k] != -1) && (pRow [j]!= -1)){
          t1 = pProcRows[i * Size + j];
          t2 = pProcRows[i * Size + k] + pRow[j];
          pProcRows[i * Size + j] = Min(t1, t2);
        }
  }
    
  delete []pRow;
}

3. Функция RowDistribution. Данная функция рассылает k -ю строку матрицы смежности всем процессам программы.

// Функция для рассылки строки всем процессам
void RowDistribution(int *pProcRows, int Size, int RowNum, int k,
  int *pRow) {
  int ProcRowRank; 	// Ранг процесса, которому принадлежит k-я строка
  int ProcRowNum;	// Номер k-й строки в полосе матрицы

  // Нахождение ранга процесса – владельца k-й строки
  int RestRows = Size;
  int Ind = 0;
  int Num = Size / ProcNum;
  
  for(ProcRowRank = 1; ProcRowRank < ProcNum + 1; ProcRowRank ++)      {
    if(k < Ind + Num ) break;
    RestRows -= Num;
    Ind      += Num;
    Num       = RestRows / (ProcNum - ProcRowRank);
  }
  ProcRowRank = ProcRowRank - 1;
  ProcRowNum  = k - Ind;

  if(ProcRowRank == ProcRank)
    // Копирование строки в массив pRow
    copy(&pProcRows[ProcRowNum * Size], &pProcRows[(ProcRowNum + 1) *
      Size], pRow);

  // Распределение k-й строки между процессами  
  MPI_Bcast(pRow, Size, MPI_INT, ProcRowRank, MPI_COMM_WORLD);
}

10.1.7. Результаты вычислительных экспериментов

Эксперименты проводились на вычислительном кластере Нижегородского университета на базе процессоров Intel Xeon 4 EM64T, 3000 МГц и сети Gigabit Ethernet под управлением операционной системы Microsoft Windows Server 2003 Standard x64 Edition и системы управления кластером Microsoft Compute Cluster Server.

Для оценки длительности базовой скалярной операции выбора минимального значения проводилось решение задачи поиска всех кратчайших путей при помощи последовательного алгоритма и полученное таким образом время вычислений делилось на общее количество выполненных операций – в результате для величины было получено значение 7,14 нсек. Эксперименты, выполненные для определения параметров сети передачи данных, показали значения латентности и пропускной способности соответственно 130 мкс и 53,29 Мбайт/с. Все вычисления производились над числовыми значениями типа int, размер которого на данной платформе равен 4 байта (следовательно, w=4 ).

Результаты вычислительных экспериментов приведены в таблице 10.1. Эксперименты выполнялись с использованием двух, четырех и восьми процессоров. Время указано в секундах.

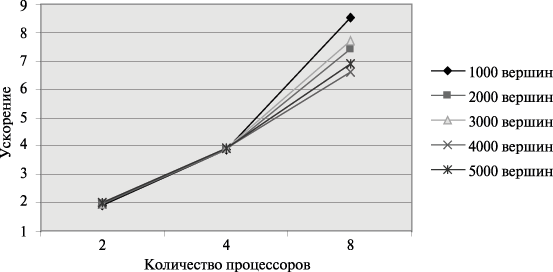
Рис. 10.4. Графики зависимости ускорения параллельного алгоритма Флойда от числа используемых процессоров при различном количестве вершин графа

Сравнение времени выполнения эксперимента 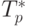и теоретической оценки T_p из (10.3) приведено в таблице 10.2 и на рис. 10.5.

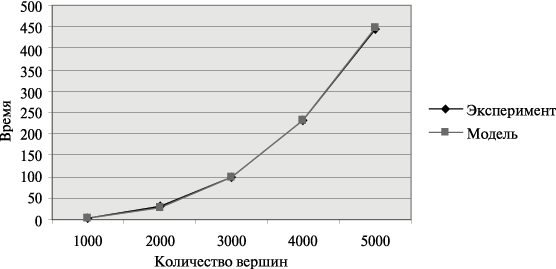
Рис. 10.5. Графики экспериментально установленного времени работы параллельного алгоритма Флойда и теоретической оценки в зависимости от количества вершин графа при использовании двух процессоров

Таблица 10.2. Сравнение экспериментального и теоретического времени работы алгоритма Флойда

Количество вершин	Последовательный алгоритм	Параллельный алгоритм
		2 процессора		4 процессора		8 процессоров
1000	8,038	3,776	4,152	2,196	2,067	1,509	0,941
2000	59,812	29,123	30,323	15,405	15,375	8,826	8,058
3000	197,111	97,465	99,264	50,336	50,232	27,307	25,643
4000	461,785	230,220	232,507	117,701	117,220	62,306	69,946
5000	884,622	448,811	443,747	228,211	224,441	119,179	128,078