Параллельные методы матричного умножения
7.5. Алгоритм Кэннона умножения матриц при блочном разделении данных
Рассмотрим еще один параллельный алгоритм матричного умножения, основанный на блочном разбиении матриц, – алгоритм Кэннона ( Cannon ).
7.5.1. Определение подзадач
Как и при рассмотрении алгоритма Фокса, в качестве базовой подзадачи выберем вычисления, связанные с определением одного из блоков результирующей матрицы C. Как уже отмечалось ранее, для вычисления элементов этого блока подзадача должна иметь доступ к элементам горизонтальной полосы матрицы А и элементам вертикальной полосы матрицы В.
7.5.2. Выделение информационных зависимостей
Отличие алгоритма Кэннона от метода Фокса состоит в изменении схемы начального распределения блоков перемножаемых матриц между подзадачами вычислительной системы. Начальное расположение блоков в алгоритме Кэннона подбирается таким образом, чтобы блоки в подзадачах могли бы быть перемножены без каких-либо дополнительных передач данных. При этом подобное распределение блоков может быть организовано таким образом, что перемещение блоков между подзадачами в ходе вычислений может осуществляться с использованием более простых коммуникационных операций.
С учетом высказанных замечаний этап инициализации алгоритма Кэннона включает выполнение следующих операций передач данных:
- в каждую подзадачу (i,j) передаются блоки Aij, Bij ;
- для каждой строки i решетки подзадач блоки матрицы A сдвигаются на (i-1) позиций влево;
- для каждого столбца j решетки подзадач блоки матрицы B сдвигаются на (j-1) позиций вверх.
Выполняемые при перераспределении матричных блоков процедуры передачи данных являются примером операции циклического сдвига – см. "Оценка коммуникационной трудоемкости параллельных алгоритмов" . Для пояснения используемого способа начального распределения данных на рис. 7.9 показан пример расположения блоков для решетки подзадач 3і3.
увеличить изображение
Рис. 7.9. Перераспределение блоков исходных матриц между процессорами при выполнении алгоритма Кэннона
В результате такого начального распределения в каждой базовой подзадаче будут располагаться блоки, которые могут быть перемножены без дополнительных операций передачи данных. Кроме того, получение всех последующих блоков для подзадач может быть обеспечено при помощи простых коммуникационных действий — после выполнения операции блочного умножения каждый блок матрицы A должен быть передан предшествующей подзадаче влево по строкам решетки подзадач, а каждый блок матрицы В – предшествующей подзадаче вверх по столбцам решетки. Как можно показать, последовательность таких циклических сдвигов и умножение получаемых блоков исходных матриц A и B приведет к получению в базовых подзадачах соответствующих блоков результирующей матрицы C.
7.5.3. Масштабирование и распределение подзадач по процессорам
Как и ранее в методе Фокса, для алгоритма Кэннона размер блоков может быть подобран таким образом, чтобы количество базовых подзадач совпадало с числом имеющихся процессоров. Поскольку объемы вычислений в каждой подзадаче являются равными, это обеспечивает полную балансировку вычислительной нагрузки между процессорами.
Для распределения подзадач между процессорами может быть применен подход, использованный в алгоритме Фокса, – множество имеющихся процессоров представляется в виде квадратной решетки и размещение базовых подзадач (i,j) осуществляется на процессорах Pi,j соответствующих узлов процессорной решетки. Необходимая структура сети передачи данных, как и ранее, может быть обеспечена на физическом уровне при топологии вычислительной системы в виде решетки или полного графа.
7.5.4. Анализ эффективности
Перед проведением анализа эффективности следует отметить, что алгоритм Кэннона отличается от метода Фокса только видом выполняемых в ходе вычислений коммуникационных операций. Как результат, используя оценки времени выполнения вычислительных операций, приведенные в п. 7.4.4, проведем только анализ коммуникационной сложности алгоритма Кэннона.
В соответствии с правилами алгоритма на этапе инициализации производится перераспределение блоков матриц А и B при помощи циклического сдвига матричных блоков по строкам и столбцам процессорной решетки. Трудоемкость выполнения такой операции передачи данных существенным образом зависит от топологии сети. Для сети со структурой полного графа все необходимые пересылки блоков могут быть выполнены одновременно (т.е. длительность операции оказывается равной времени передачи одного матричного блока между соседними процессорами). Для сети с топологией гиперкуба операция циклического сдвига может потребовать выполнения log2q итераций. Для сети с кольцевой структурой связей необходимое количество итераций оказывается равным q-1 – более подробно методы выполнения операции циклического сдвига рассмотрены в "Оценка коммуникационной трудоемкости параллельных алгоритмов" . Используем для построения оценки коммуникационной сложности этапа инициализации вариант топологии полного графа как более соответствующего кластерным вычислительным системам, время выполнения начального перераспределения блоков может оцениваться как
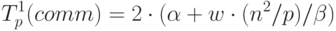 |
( 7.14) |
Оценим теперь затраты на передачу данных между процессорами при выполнении основной части алгоритма Кэннона. На каждой итерации алгоритма после умножения матричных блоков процессоры передают свои блоки предыдущим процессорам по строкам (для блоков матрицы A ) и столбцам (для блоков матрицы B ) процессорной решетки. Эти операции также могут быть выполнены процессорами параллельно, и, тем самым, длительность таких коммуникационных действий составляет:

Поскольку количество итераций алгоритма Кэннона равно q, то с учетом оценки (7.10) общее время выполнения параллельных вычислений может быть определено при помощи следующего соотношения:
![T_p=q[(n^2/p)\cdot(2n/q-1)+(n^2/p)]\cdot\tau+(2q+2)(\alpha+w(n^2/p)/ \beta)](/sites/default/files/tex_cache/cc9e6d81f4bcfc54b3c5f53e4cbac7fb.png) |
( 7.16) |
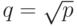 определяет размер
процессорной решетки).
определяет размер
процессорной решетки).7.5.5. Результаты вычислительных экспериментов
Вычислительные эксперименты для оценки эффективности параллельного алгоритма проводились при тех же условиях, что и ранее выполненные (см. п. 7.3.5). Результаты экспериментов для случаев четырех и девяти процессоров приведены в таблице 7.5.
Сравнение времени выполнения эксперимента 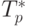 и теоретического
времени Tp, вычисленного в соответствии с выражением (7.16),
представлено в таблице 7.6 и на рис. 7.11.
и теоретического
времени Tp, вычисленного в соответствии с выражением (7.16),
представлено в таблице 7.6 и на рис. 7.11.
| Размер матриц | 4 процессора | 9 процессоров | ||
|---|---|---|---|---|
 |
 |
 |
 |
|
| 1000 | 3,4485 | 3,0806 | 1,5669 | 1,1889 |
| 1500 | 11,3821 | 11,1716 | 5,1348 | 4,6310 |
| 2000 | 26,6769 | 24,0502 | 11,9912 | 14,4759 |
| 2500 | 51,7488 | 53,1444 | 23,2098 | 23,5398 |
| 3000 | 89,0138 | 88,2979 | 39,8643 | 36,3688 |



