Параллельные методы матричного умножения
7.3.3. Масштабирование и распределение подзадач по процессорам
Выделенные базовые подзадачи характеризуются одинаковой вычислительной трудоемкостью и равным объемом передаваемых данных. Когда размер матриц n оказывается больше, чем число процессоров p, базовые подзадачи можно укрупнить, объединив в рамках одной подзадачи несколько соседних строк и столбцов перемножаемых матриц. В этом случае исходная матрица A разбивается на ряд горизонтальных полос, а матрица B представляется в виде набора вертикальных (для первого алгоритма) или горизонтальных (для второго алгоритма) полос. Размер полос при этом следует выбрать равным k=n/p (в предположении, что n кратно p ), что позволит по-прежнему обеспечить равномерность распределения вычислительной нагрузки по процессорам, составляющим многопроцессорную вычислительную систему.
Для распределения подзадач между процессорами может быть использован любой способ, обеспечивающий эффективное представление кольцевой структуры информационного взаимодействия подзадач. Для этого достаточно, например, чтобы подзадачи, являющиеся соседними в кольцевой топологии, располагались на процессорах, между которыми имеются прямые линии передачи данных.
7.3.4. Анализ эффективности
Выполним анализ эффективности первого параллельного алгоритма умножения матриц.
Общая трудоемкость последовательного алгоритма, как уже отмечалось ранее, является пропорциональной n3. Для параллельного алгоритма на каждой итерации каждый процессор выполняет умножение имеющихся на процессоре полос матрицы А и матрицы В (размер полос равен n/p, и, как результат, общее количество выполняемых при этом умножении операций равно n3/p2 ). Поскольку число итераций алгоритма совпадает с количеством процессоров, сложность параллельного алгоритма без учета затрат на передачу данных может быть определена при помощи выражения
 |
( 7.4) |
С учетом этой оценки показатели ускорения и эффективности данного параллельного алгоритма матричного умножения принимают вид:
 |
( 7.5) |
Таким образом, общий анализ сложности дает идеальные показатели эффективности параллельных вычислений. Для уточнения полученных соотношений оценим более точно количество вычислительных операций алгоритма и учтем затраты на выполнение операций передачи данных между процессорами.
С учетом числа и длительности выполняемых операций время выполнения вычислений параллельного алгоритма может быть оценено следующим образом:
 |
( 7.6) |
 есть время выполнения одной элементарной
скалярной операции).
есть время выполнения одной элементарной
скалярной операции).Для оценки коммуникационной сложности параллельных вычислений будем предполагать, что все операции передачи данных между процессорами в ходе одной итерации алгоритма могут быть выполнены параллельно. Объем передаваемых данных между процессорами определяется размером полос и составляет n/p строк или столбцов длины n. Общее количество параллельных операций передачи сообщений на единицу меньше числа итераций алгоритма (на последней итерации передача данных не является обязательной). Тем самым, оценка трудоемкости выполняемых операций передачи данных может быть определена как
 |
( 7.7) |
 – латентность,
– латентность,  – пропускная способность сети передачи
данных, а w есть размер элемента матрицы в байтах.
– пропускная способность сети передачи
данных, а w есть размер элемента матрицы в байтах.С учетом полученных соотношений общее время выполнения параллельного алгоритма матричного умножения определяется следующим выражением:
 |
( 7.8) |
7.3.5. Результаты вычислительных экспериментов
Эксперименты проводились на вычислительном кластере на базе процессоров Intel Xeon 4 EM64T, 3000 МГц и сети Gigabit Ethernet под управлением операционной системы Microsoft Windows Server 2003 Standard x64 Edition и системы управления кластером Microsoft Compute Cluster Server.
Для оценки длительности  базовой скалярной операции
проводилось решение задачи умножения матриц при помощи
последовательного алгоритма и полученное таким образом время
вычислений делилось на общее количество выполненных операций – в
результате подобных экспериментов для величины
базовой скалярной операции
проводилось решение задачи умножения матриц при помощи
последовательного алгоритма и полученное таким образом время
вычислений делилось на общее количество выполненных операций – в
результате подобных экспериментов для величины  было получено
значение 6,4 нсек. Эксперименты, выполненные для определения
параметров сети передачи данных, показали значения латентности a
и пропускной способности b соответственно 130 мкс и 53,29
Мбайт/с. Все вычисления производились над числовыми значениями
типа double, т.е. величина w равна 8 байт.
было получено
значение 6,4 нсек. Эксперименты, выполненные для определения
параметров сети передачи данных, показали значения латентности a
и пропускной способности b соответственно 130 мкс и 53,29
Мбайт/с. Все вычисления производились над числовыми значениями
типа double, т.е. величина w равна 8 байт.
Результаты вычислительных экспериментов приведены в таблице 7.1. Эксперименты выполнялись с использованием двух, четырех и восьми процессоров.
| Размер матрицы | Последовательный алгоритм | Параллельный алгоритм | |||||
|---|---|---|---|---|---|---|---|
| 2 процессора | 4 процессора | 8 процессоров | |||||
| Время | Ускорение | Время | Ускорение | Время | Ускорение | ||
| 500 | 0,8752 | 0,3758 | 2,3287 | 0,1535 | 5,6982 | 0,0968 | 9,0371 |
| 1000 | 12,8787 | 5,4427 | 2,3662 | 2,2628 | 5,6912 | 0,6998 | 18,4014 |
| 1500 | 43,4731 | 20,9503 | 2,0750 | 11,0804 | 3,9234 | 5,1766 | 8,3978 |
| 2000 | 103,0561 | 45,7436 | 2,2529 | 21,6001 | 4,7710 | 9,4127 | 10,9485 |
| 2500 | 201,2915 | 99,5097 | 2,0228 | 56,9203 | 3,5363 | 18,3303 | 10,9813 |
| 3000 | 347,8434 | 171,9232 | 2,0232 | 111,9642 | 3,1067 | 45,5482 | 7,6368 |

Рис. 7.4. Зависимость ускорения от количества процессоров при выполнении первого параллельного алгоритма матричного умножения при ленточной схеме распределения данных
Сравнение экспериментального времени 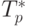 выполнения
эксперимента и теоретического времени Tp из формулы (7.8)
представлено в таблице 7.2 и на рис. 7.5.
выполнения
эксперимента и теоретического времени Tp из формулы (7.8)
представлено в таблице 7.2 и на рис. 7.5.

Рис. 7.5. График зависимости от объема исходных данных теоретического и экспериментального времени выполнения параллельного алгоритма на двух процессорах (ленточная схема разбиения данных)
| Размер матрицы | 2 процессора | 4 процессора | 8 процессоров | |||
|---|---|---|---|---|---|---|
 |
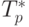 |
 |
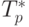 |
 |
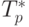 |
|
| 500 | 0,8243 | 0,3758 | 0,4313 | 0,1535 | 0,2353 | 0,0968 |
| 1000 | 6,51822 | 5,4427 | 3,3349 | 2,2628 | 1,7436 | 0,6998 |
| 1500 | 21,9137 | 20,9503 | 11,1270 | 11,0804 | 5,7340 | 5,1766 |
| 2000 | 51,8429 | 45,7436 | 26,2236 | 21,6001 | 13,4144 | 9,4127 |
| 2500 | 101,1377 | 99,5097 | 51,0408 | 56,9203 | 25,9928 | 18,3303 |
| 3000 | 174,6301 | 171,9232 | 87,9946 | 111,9642 | 44,6772 | 45,5482 |
