Параллельные методы матричного умножения
7.4.5. Программная реализация
Представим возможный вариант программной реализации алгоритма Фокса для умножения матриц при блочном представлении данных. Приводимый программный код содержит основные модули параллельной программы, отсутствие отдельных вспомогательных функций не сказывается на общем понимании реализуемой схемы параллельных вычислений.
1. Главная функция программы. Определяет основную логику работы алгоритма, последовательно вызывает необходимые подпрограммы.
// Программа 7.1
// Алгоритм Фокса умножения матриц – блочное представление данных
// Условия выполнения программы: все матрицы квадратные,
// размер блоков и их количество по горизонтали и вертикали
// одинаково, процессы образуют квадратную решетку
int ProcNum = 0; // Количество доступных процессов
int ProcRank = 0; // Ранг текущего процесса
int GridSize; // Размер виртуальной решетки процессов
int GridCoords[2]; // Координаты текущего процесса в процессной
// решетке
MPI_Comm GridComm; // Коммуникатор в виде квадратной решетки
MPI_Comm ColComm; // коммуникатор – столбец решетки
MPI_Comm RowComm; // коммуникатор – строка решетки
void main ( int argc, char * argv[] ) {
double* pAMatrix; // Первый аргумент матричного умножения
double* pBMatrix; // Второй аргумент матричного умножения
double* pCMatrix; // Результирующая матрица
int Size; // Размер матриц
int BlockSize; // Размер матричных блоков, расположенных
// на процессах
double *pAblock; // Блок матрицы А на процессе
double *pBblock; // Блок матрицы В на процессе
double *pCblock; // Блок результирующей матрицы С на процессе
double *pMatrixAblock;
double Start, Finish, Duration;
setvbuf(stdout, 0, _IONBF, 0);
MPI_Init(&argc, &argv);
MPI_Comm_size(MPI_COMM_WORLD, &ProcNum);
MPI_Comm_rank(MPI_COMM_WORLD, &ProcRank);
GridSize = sqrt((double)ProcNum);
if (ProcNum != GridSize*GridSize) {
if (ProcRank == 0) {
printf ("Number of processes must be a perfect square \n");
}
}
else {
if (ProcRank == 0)
printf("Parallel matrix multiplication program\n");
// Создание виртуальной решетки процессов и коммуникаторов
// строк и столбцов
CreateGridCommunicators();
// Выделение памяти и инициализация элементов матриц
ProcessInitialization ( pAMatrix, pBMatrix, pCMatrix, pAblock,
pBblock, pCblock, pMatrixAblock, Size, BlockSize );
// Блочное распределение матриц между процессами
DataDistribution(pAMatrix, pBMatrix, pMatrixAblock, pBblock, Size,
BlockSize);
// Выполнение параллельного метода Фокса
ParallelResultCalculation(pAblock, pMatrixAblock, pBblock,
pCblock, BlockSize);
// Сбор результирующей матрицы на ведущем процессе
ResultCollection(pCMatrix, pCblock, Size, BlockSize);
// Завершение процесса вычислений
ProcessTermination (pAMatrix, pBMatrix, pCMatrix, pAblock, pBblock,
pCblock, pMatrixAblock);
}
MPI_Finalize();
}
7.1.
2. Функция CreateGridCommunicators. Данная функция создает коммуникатор в виде двумерной квадратной решетки, определяет координаты каждого процесса в этой решетке, а также создает коммуникаторы отдельно для каждой строки и каждого столбца.
Создание решетки производится при помощи функции MPI_Cart_create (вектор Periodic определяет возможность передачи сообщений между граничными процессами строк и столбцов создаваемой решетки). После создания решетки каждый процесс параллельной программы будет иметь координаты своего положения в решетке; получение этих координат обеспечивается при помощи функции MPI_Cart_coords.
Формирование топологий завершается созданием множества коммуникаторов для каждой строки и каждого столбца решетки в отдельности (функция MPI_Cart_sub ).
// Создание коммуникатора в виде двумерной квадратной решетки
// и коммуникаторов для каждой строки и каждого столбца решетки
void CreateGridCommunicators() {
int DimSize[2]; // Количество процессов в каждом измерении
// решетки
int Periodic[2]; // =1 для каждого измерения, являющегося
// периодическим
int Subdims[2]; // =1 для каждого измерения, оставляемого
// в подрешетке
DimSize[0] = GridSize;
DimSize[1] = GridSize;
Periodic[0] = 0;
Periodic[1] = 0;
// Создание коммуникатора в виде квадратной решетки
MPI_Cart_create(MPI_COMM_WORLD, 2, DimSize, Periodic, 1, &GridComm);
// Определение координат процесса в решетке
MPI_Cart_coords(GridComm, ProcRank, 2, GridCoords);
// Создание коммуникаторов для строк процессной решетки
Subdims[0] = 0; // Фиксация измерения
Subdims[1] = 1; // Наличие данного измерения в подрешетке
MPI_Cart_sub(GridComm, Subdims, &RowComm);
// Создание коммуникаторов для столбцов процессной решетки
Subdims[0] = 1;
Subdims[1] = 0;
MPI_Cart_sub(GridComm, Subdims, &ColComm);
}
7.2.
3. Функция ProcessInitialization. Данная функция определяет параметры решаемой задачи (размеры матриц и их блоков), выделяет память для хранения данных и осуществляет ввод исходных матриц (или формирует их при помощи какого-либо датчика случайных чисел). Всего в каждом процессе должна быть выделена память для хранения четырех блоков – для указателей на выделенную память используются переменные pAblock, pBblock, pCblock, pMatrixAblock. Первые три указателя определяют блоки матриц A, B и C соответственно. Следует отметить, что содержимое блоков pAblock и pBblock постоянно меняется в соответствии с пересылкой данных между процессами, в то время как блок pMatrixAblock матрицы A остается неизменным и применяется при рассылках блоков по строкам решетки процессов (см. функцию AblockCommunication ).
Для определения элементов исходных матриц будем использовать функцию RandomDataInitialization, реализацию которой читателю предстоит выполнить самостоятельно.
// Функция для выделения памяти и инициализации исходных данных
void ProcessInitialization (double* &pAMatrix, double* &pBMatrix,
double* &pCMatrix, double* &pAblock, double* &pBblock,
double* &pCblock, double* &pTemporaryAblock, int &Size,
int &BlockSize ) {
if (ProcRank == 0) {
do {
printf("\nВведите размер матриц: ");
scanf("%d", &Size);
if (Size%GridSize != 0) {
printf ("Размер матриц должен быть кратен размеру сетки! \n");
}
}
while (Size%GridSize != 0);
}
MPI_Bcast(&Size, 1, MPI_INT, 0, MPI_COMM_WORLD);
BlockSize = Size/GridSize;
pAblock = new double [BlockSize*BlockSize];
pBblock = new double [BlockSize*BlockSize];
pCblock = new double [BlockSize*BlockSize];
pTemporaryAblock = new double [BlockSize*BlockSize];
for (int i=0; i<BlockSize*BlockSize; i++) {
pCblock[i] = 0;
}
if (ProcRank == 0) {
pAMatrix = new double [Size*Size];
pBMatrix = new double [Size*Size];
pCMatrix = new double [Size*Size];
RandomDataInitialization(pAMatrix, pBMatrix, Size);
}
}
7.3.
4. Функции DataDistribution и ResultCollection. После задания исходных матриц на нулевом процессе необходимо осуществить распределение исходных данных. Для этого предназначена функция DataDistribution. Может быть предложено два способа выполнения блочного разделения матриц между процессорами, организованными в двумерную квадратную решетку. В первом из них для организации передачи блоков в рамках одной и той же коммуникационной операции можно сформировать средствами MPI производный тип данных. Во втором способе можно организовать двухэтапную процедуру. На первом этапе матрица разделяется на горизонтальные полосы. Эти полосы распределяются на процессы, составляющие нулевой столбец процессорной решетки. Далее каждая полоса разделяется на блоки между процессами, составляющими строки процессорной решетки.
Для выполнения сбора результирующей матрицы из блоков предназначена функция ResultCollection. Сбор данных также можно выполнить либо с использованием производного типа данных, либо при помощи двухэтапной процедуры, зеркально отображающей процедуру распределения матрицы.
Реализация функций DataDistribution и ResultCollection представляет собой задание для самостоятельной работы.
5. Функция AblockCommunication. Функция выполняет рассылку блоков матрицы A по строкам процессорной решетки. Для этого в каждой строке решетки определяется ведущий процесс Pivot, осуществляющий рассылку. Для рассылки используется блок pMatrixAblock, переданный в процесс в момент начального распределения данных. Выполнение операции рассылки блоков осуществляется при помощи функции MPI_Bcast. Следует отметить, что данная операция является коллективной и ее локализация пределами отдельных строк решетки обеспечивается за счет использования коммуникаторов RowComm, определенных для набора процессов каждой строки решетки в отдельности.
// Рассылка блоков матрицы А по строкам решетки процессов
void ABlockCommunication (int iter, double *pAblock,
double* pMatrixAblock, int BlockSize) {
// Определение ведущего процесса в строке процессной решетки
int Pivot = (GridCoords[0] + iter) % GridSize;
// Копирование передаваемого блока в отдельный буфер памяти
if (GridCoords[1] == Pivot) {
for (int i=0; i<BlockSize*BlockSize; i++)
pAblock[i] = pMatrixAblock[i];
}
// Рассылка блока
MPI_Bcast(pAblock, BlockSize*BlockSize, MPI_DOUBLE, Pivot,
RowComm);
}6. Функция BlockMultiplication. Функция обеспечивает перемножение блоков матриц A и B. Следует отметить, что для более легкого понимания рассматриваемой программы приводится простой вариант реализации функции – выполнение операции блочного умножения может быть существенным образом оптимизировано для сокращения времени вычислений. Данная оптимизация может быть направлена, например, на повышение эффективности использования кэша процессоров, векторизации выполняемых операций и т.п.
// Умножение матричных блоков
void BlockMultiplication (double *pAblock, double *pBblock,
double *pCblock, int BlockSize) {
// Вычисление произведения матричных блоков
for (int i=0; i<BlockSize; i++) {
for (int j=0; j<BlockSize; j++) {
double temp = 0;
for (int k=0; k<BlockSize; k++ )
temp += pAblock [i*BlockSize + k] * pBblock [k*BlockSize + j];
pCblock [i*BlockSize + j] += temp;
}
}
}7. Функция BblockCommunication. Функция выполняет циклический сдвиг блоков матрицы B по столбцам процессорной решетки. Каждый процесс передает свой блок следующему процессу NextProc в столбце процессов и получает блок, переданный из предыдущего процесса PrevProc в столбце решетки. Выполнение операций передачи данных осуществляется при помощи функции MPI_SendRecv_replace, которая обеспечивает все необходимые пересылки блоков, используя при этом один и тот же буфер памяти pBblock. Кроме того, эта функция гарантирует отсутствие возможных тупиков, когда операции передачи данных начинают одновременно выполняться несколькими процессами при кольцевой топологии сети.
// Циклический сдвиг блоков матрицы В вдоль столбца процессной
// решетки
void BblockCommunication (double *pBblock, int BlockSize) {
MPI_Status Status;
int NextProc = GridCoords[0] + 1;
if ( GridCoords[0] == GridSize-1 ) NextProc = 0;
int PrevProc = GridCoords[0] - 1;
if ( GridCoords[0] == 0 ) PrevProc = GridSize-1;
MPI_Sendrecv_replace( pBblock, BlockSize*BlockSize, MPI_DOUBLE,
NextProc, 0, PrevProc, 0, ColComm, &Status);
}8. Функция ParallelResultCalculation. Для непосредственного выполнения параллельного алгоритма Фокса умножения матриц предназначена функция ParallelResultCalculation, которая реализует логику работы алгоритма.
// Функция для параллельного умножения матриц
void ParallelResultCalculation(double* pAblock, double* pMatrixAblock,
double* pBblock, double* pCblock, int BlockSize) {
for (int iter = 0; iter < GridSize; iter ++) {
// Рассылка блоков матрицы A по строкам процессной решетки
ABlockCommunication (iter, pAblock, pMatrixAblock, BlockSize);
// Умножение блоков
BlockMultiplication(pAblock, pBblock, pCblock, BlockSize);
// Циклический сдвиг блоков матрицы B в столбцах процессной
// решетки
BblockCommunication(pBblock, BlockSize);
}
}7.4.6. Результаты вычислительных экспериментов
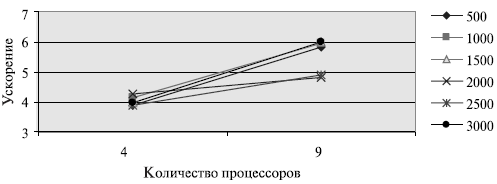
Вычислительные эксперименты для оценки эффективности параллельного алгоритма проводились при тех же условиях, что и ранее выполненные (см. п. 7.3.5). Результаты экспериментов с использованием четырех и девяти процессоров приведены в таблице 7.3.
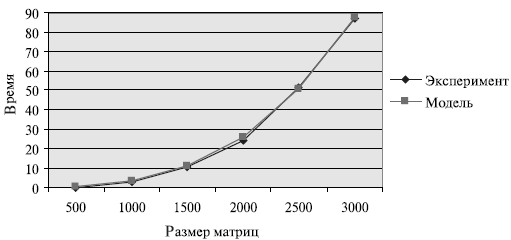
Рис. 7.8. График зависимости экспериментального и теоретического времени выполнения алгоритма Фокса на четырех процессорах
| Размер матриц | 4 процессора | 9 процессоров | ||
|---|---|---|---|---|
 |
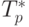 |
 |
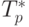 |
|
| 500 | 0,4217 | 0,2190 | 0,2200 | 0,1468 |
| 1000 | 3,2970 | 3,0910 | 1,5924 | 2,1565 |
| 1500 | 11,0419 | 10,8678 | 5,1920 | 7,2502 |
| 2000 | 26,0726 | 24,1421 | 12,0927 | 21,4157 |
| 2500 | 50,8049 | 51,4735 | 23,3682 | 41,2159 |
| 3000 | 87,6548 | 87,0538 | 40,0923 | 58,2022 |
Сравнение времени выполнения эксперимента 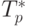 и теоретического
времени Tp, вычисленного в соответствии с выражением (7.13),
представлено в таблице 7.4 и на рис. 7.8.
и теоретического
времени Tp, вычисленного в соответствии с выражением (7.13),
представлено в таблице 7.4 и на рис. 7.8.