Синтаксический разбор слева направо (LR)

16.3. SLR(1)-грамматики

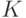Напомним, что для любого нетерминала K мы определяли (см. "пункт 15.3." ) множество тех терминалов, которые могут стоять непосредственно за в выводимом (из начального нетерминала) слове; в это множество добавляют также символ EOI, если нетерминал K может стоять в конце выводимого слова.

16.3.1. Доказать, что если в данный момент LR-процесса последний символ стека S равен K, причем процесс этот может в дальнейшем успешно завершиться, то Next принадлежит .

Решение. Этот факт является непосредственным следствием определения (вспомним соответствие между правыми выводами и LR-процессами).

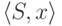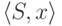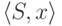Рассмотрим некоторую грамматику, произвольное слово S из терминалов и нетерминалов и терминал x. Если множество содержит ситуацию, в которой справа от подчеркивания стоит терминал x, то говорят, что для пары возможен сдвиг. Если в есть ситуация ,, причем x принадлежит , то говорят, что для пары SLR(1)-возможна свертка (по правилу ). Говорят, что для пары возникает SLR(1)-конфликт типа сдвиг/свертка, если возможны и сдвиг, и свертка. Говорят, что для пары 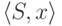возникает SLR(1)-конфликт типа свертка/свертка, если есть несколько правил, по которым возможна свертка.

Грамматика называется SLR(1)-грамматикой, если в ней нет SLR(1)-конфликтов типа сдвиг/свертка и свертка/свертка ни для одной пары .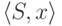

16.3.2. Пусть дана SLR(1)-грамматика. Доказать, что у любого слова существует не более одного правого вывода. Построить алгоритм проверки выводимости в SLR(1)-грамматике.

Решение. Аналогично случаю LR(0)-грамматик, только при выборе между сдвигом и сверткой учитывается очередной символ ( Next ).

16.3.3. Проверить, является ли приведенная выше в "задаче 16.1.10." грамматика (с нетерминалами E, T и F ) SLR(1)-грамматикой.

Решение. Да, является, так как оба конфликта, мешающие ей быть LR(0)-грамматикой, разрешаются с учетом очередного символа: и для слова T, и для слова E+T сдвиг возможен только при , а символ * не принадлежит ни , ни 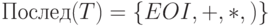, и поэтому при свертка невозможна.

16.4. LR(1)-грамматики, LALR(1)-грамматики

Описанный выше SLR(1)-подход используют не всю возможную информацию при выяснении того, возможна ли свертка. Именно, он отдельно проверяет, возможна ли свертка при данном состоянии стека S и отдельно - возможна ли свертка по данному правилу при данном символе Next. Между тем эти проверки не являются независимыми: обе могут дать положительный ответ, но тем не менее свертка при стеке S и очередном символе Next невозможна. В LR(1)-подходе этот недостаток устраняется.

LR(1)-подход состоит вот в чем: все наши определения и утверждения модифицируются так, чтобы учесть, какой символ стоит справа от разворачиваемого нетерминала (другими словами, чему равен Next при свертке).

Пусть - одно из правил грамматики, а t - некоторый терминал или спецсимвол EOI (который мы домысливаем в конце входного слова). Определим множество 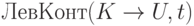как множество всех слов, которые являются содержимым стека непосредственно перед сверткой U в K в ходе успешного LR-процесса, при условии (в момент свертки).

Если отбросить у всех слов из 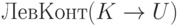их конец U, то получится множество всех слов, которые могут появиться в правых выводах перед нетерминалом K, за которым стоит символ t. Это множество (не зависящее от того, какое из правил для нетерминала K выбрано) мы будем обозначать .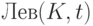

16.4.1. Написать грамматику для порождения множеств .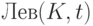

Решение. Ее нетерминалами будут символы для каждого нетерминала K и для каждого терминала t (а также для 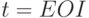). Ее правила таковы. Пусть P - начальный нетерминал исходной грамматики. Тогда в новой грамматике будет правило

Каждое правило исходной грамматики порождает несколько правил новой. Например, для правила ( L, M, N - нетерминалы, u - терминал) в новую грамматику мы добавим правила (для всех терминалов x ); (для всех s, которые могут начинать слова, выводимые из N, и для всех y, а также для всех пар , если из N выводимо пустое слово); (для всех терминалов s ).

16.4.2. Как меняется определение ситуации?

Решение. Ситуацией называется пара