Разные алгоритмы на графах
9.1.7.
Известно, что все цены неотрицательны. Найти наименьшую
стоимость проезда 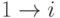 для всех
для всех 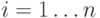 за время
за время  .
.
Решение. В процессе работы алгоритма некоторые города будут выделенными (в начале - только город 1, в конце - все). При этом:
- для каждого выделенного города i хранится
наименьшая стоимость пути
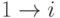 ; при этом
известно, что минимум достигается на пути, проходящем
только через выделенные города;
; при этом
известно, что минимум достигается на пути, проходящем
только через выделенные города; - для каждого невыделенного города i хранится
наименьшая стоимость пути
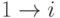 ,
в котором в качестве промежуточных используются только
выделенные города.
,
в котором в качестве промежуточных используются только
выделенные города.
Множество выделенных городов расширяется на основании следующего замечания: если среди всех невыделенных городов взять тот, для которого хранимое число минимально, то это число является истинной наименьшей стоимостью. В самом деле, пусть есть более короткий путь. Рассмотрим первый невыделенный город на этом пути - уже до него путь длиннее! (Здесь существенна неотрицательность цен.)
Добавив выбранный город к выделенным, мы должны скорректировать информацию, хранимую для невыделенных городов. При этом достаточно учесть лишь пути, в которых новый город является последним пунктом пересадки, а это легко сделать, так как минимальную стоимость проезда в новый город мы уже знаем.
При самом бесхитростном способе хранения множества
выделенных городов (в булевском векторе) добавление одного
города к числу выделенных требует времени  .
.
Этот алгоритм называют алгоритмом Дейкстры.
9.1.8.
Имеется  городов, соединенных дорогами (с односторонним
движением). Для любых городов
городов, соединенных дорогами (с односторонним
движением). Для любых городов  известен максимальный
вес груза, который можно везти из
известен максимальный
вес груза, который можно везти из  в
в  (грузоподъемность
дороги). Найти за время
(грузоподъемность
дороги). Найти за время 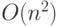 для всех городов максимальный
вес груза, который в них можно привезти из столицы.
для всех городов максимальный
вес груза, который в них можно привезти из столицы.
Указание. Действовать аналогично алгоритму Дейкстры, заменив сумму на максимум.
Отыскание кратчайшего пути имеет естественную интерпретацию
в терминах матриц. Пусть  - матрица цен одной авиакомпании, а
- матрица цен одной авиакомпании, а  - матрица цен другой. Пусть мы хотим лететь с одной пересадкой, причем сначала самолетом компании
- матрица цен другой. Пусть мы хотим лететь с одной пересадкой, причем сначала самолетом компании  , а затем -
компании
, а затем -
компании  . Сколько нам придется заплатить, чтобы попасть
из города i в город j?
. Сколько нам придется заплатить, чтобы попасть
из города i в город j?
9.1.9. Доказать, что эта матрица вычисляется по обычной формуле для произведения матриц, только вместо суммы надо брать минимум, а вместо умножения - сумму.
9.1.10. Доказать, что таким образом определенное произведение матриц ассоциативно.
9.1.11.
Доказать, что задача о кратчайших путях эквивалентна
вычислению 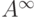 для матрицы цен
для матрицы цен  :
в последовательности
:
в последовательности 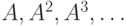 все элементы,
начиная с некоторого, равны искомой матрице стоимостей
кратчайших путей. (Если нет отрицательных циклов!)
все элементы,
начиная с некоторого, равны искомой матрице стоимостей
кратчайших путей. (Если нет отрицательных циклов!)
9.1.12. Начиная с какого элемента можно гарантировать равенство в предыдущей задаче?
Обычное (не модифицированное) умножение матриц тоже может оказаться полезным, только матрицы должны быть другие. Пусть есть не все рейсы (как раньше), а только некоторые, a[i][j] равно 1, если рейс есть, и 0, если рейса нет. Возведем матрицу a (обычным образом) в степень k и посмотрим на ее ( i - j )-ый элемент.
9.1.13. Чему он равен?
Ответ. Числу различных способов попасть из i в j за k рейсов (с k-1 пересадками).
При описании кратчайших путей случай, когда есть не все
рейсы, можно свести к исходному, введя фиктивные рейсы
с бесконечно большой (или достаточно большой) стоимостью.
Тем не менее возникает такой вопрос. Число реальных рейсов
может быть существенно меньше 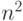 , поэтому интересны
алгоритмы, которые работают эффективно в такой ситуации.
Исходные данные естественно представлять тогда в такой
форме: для каждого города известно число выходящих из него
рейсов, их пункты назначения и цены.
, поэтому интересны
алгоритмы, которые работают эффективно в такой ситуации.
Исходные данные естественно представлять тогда в такой
форме: для каждого города известно число выходящих из него
рейсов, их пункты назначения и цены.
9.1.14.
Доказать, что алгоритм Дейкстры можно модифицировать так,
чтобы для  городов и
городов и  рейсов (всего) он требовал не более
рейсов (всего) он требовал не более 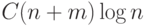 операций.
операций.
Указание.
Что надо сделать на каждом шаге? Выбрать невыделенный город
с минимальной стоимостью и скорректировать цены для всех
городов, в которые из него есть маршруты. Если бы кто-то
сообщал нам, для какого города стоимость минимальна, то
хватило бы 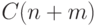 действий. А поддержание сведений о том,
какой элемент в массиве минимален (см. задачу из
"пункта 6.4."
) обходится еще в множитель
действий. А поддержание сведений о том,
какой элемент в массиве минимален (см. задачу из
"пункта 6.4."
) обходится еще в множитель  .
.
