Как обойтись без рекурсии

8.2. Стек отложенных заданий

Другой прием устранения рекурсии продемонстрируем на примере задачи о ханойских башнях.

8.2.1. Написать нерекурсивную программу для нахождения последовательности перемещений колец в задаче о ханойских башнях.

Решение. Вспомним рекурсивную программу, перекладывающую i верхних колец с m на n:

procedure move(i,m,n: integer);
| var s: integer;
begin
| if i = 1 then begin
| | writeln ('сделать ход ', m, '->', n);
| end else begin
| | s:=6-m-n; {s - третий стержень: сумма номеров равна 6}
| | move (i-1, m, s);
| | writeln ('сделать ход ', m, '->', n);
| | move (i-1, s, n);
| end;
end;

Видно, что задача "переложить i верхних дисков с m -го стержня на n -ый" сводится к трем задачам того же типа: двум задачам с i-1 дисками и к одной задаче с единственным диском. Занимаясь этими задачами, важно не позабыть, что еще осталось сделать.

Для этой цели заведем стек отложенных заданий, элементами которого будут тройки 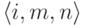. Каждая такая тройка интерпретируется как заказ "переложить i верхних дисков с m -го стержня на n -ый". Заказы упорядочены в соответствии с требуемым порядком их выполнения: самый срочный - вершина стека. Получаем такую программу:

procedure move(i,m,n: integer);
begin
| сделать стек заказов пустым
| положить в стек тройку <i,m,n>
| {инвариант: осталось выполнить заказы в стеке}
| while стек непуст do begin
| | удалить верхний элемент, переложив его в <j,p,q>
| | if j = 1 then begin
| | | writeln ('сделать ход', p, '->', q);
| | end else begin
| | | s:=6-p-q;
| | |      {s - третий стержень: сумма номеров равна 6}
| | | положить в стек тройки <j-1,s,q>, <1,p,q>, <j-1,p,s>
| | end;
| end;
end;

(Заметим, что первой в стек кладется тройка, которую надо выполнять последней.) Стек троек может быть реализован как три отдельных стека. (Кроме того, в паскале есть специальный тип, называемый "запись" ( record ), который может быть применен.)

8.2.2. (Сообщил А.К.Звонкин со ссылкой на Анджея Лисовского.) Для задачи о ханойских башнях есть и другие нерекурсивные алгоритмы. Вот один из них: простаивающим стержнем (не тем, с которого переносят, и не тем, на который переносят) должны быть все стержни по очереди. Другое правило: поочередно перемещать наименьшее кольцо и не наименьшее кольцо, причем наименьшее - по кругу.

8.2.3. Использовать замену рекурсии стеком отложенных заданий в рекурсивной программе печати десятичной записи целого числа.

Решение. Цифры добываются с конца и закладываются в стек, а затем печатаются в обратном порядке.

8.2.4. Написать нерекурсивную программу, печатающую все вершины двоичного дерева.

Решение. В этом случае стек отложенных заданий будет содержать заказы двух сортов: "напечатать данную вершину" и "напечатать все вершины поддерева с данным корнем" (при этом nil считается корнем пустого дерева). Таким образом, элемент стека есть пара: 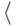тип заказа, номер вершины .

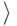Вынимая элемент из стека, мы либо сразу исполняем его (если это заказ первого типа), либо помещаем в стек три порожденных им заказа - в одном из шести возможных порядков.

8.2.5. Что изменится, если требуется не печатать вершины двоичного дерева, а подсчитать их количество?

Решение. Печатание вершины следует заменить прибавлением единицы к счетчику. Другими словами, инвариант таков: (общее число вершин=счетчик+сумма чисел вершин в поддеревьях, корни которых лежат в стеке).

8.2.6. Для некоторых из шести возможных порядков возможны упрощения, делающие ненужным хранение в стеке элементов двух видов. Указать некоторые из них.

Решение. Если требуемый порядок таков:

Несколько более сложная конструкция применима для порядка

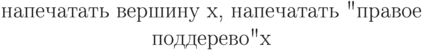
То же самое, разумеется, верно, если поменять местами левое и правое - получается еще два порядка.

Замечание. Другую программу печати всех вершин дерева можно построить на основе программы обхода дерева, разобранной в "лекции 3" . Там используется команда "вниз". Поскольку теперешнее представление дерева с помощью массивов l и r не позволяет найти предка заданной вершины, придется хранить список всех вершин на пути от корня к текущей вершине. Смотри также "лекцию 9"

8.2.7. Написать нерекурсивный вариант программы быстрой сортировки (см. "лекцию 7" ). Как обойтись стеком, глубина которого ограничена , где - число сортируемых элементов?

Решение. В стек кладутся пары 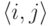, интерпретируемые как отложенные задания на сортировку соответствующих участков массива. Все эти заказы не пересекаются, поэтому размер стека не может превысить . Чтобы ограничиться стеком логарифмической глубины, будем придерживаться такого правила: глубже в стек помещать больший из возникающих двух заказов. Пусть 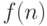- максимальная глубина стека, которая может встретиться при сортировке массива из не более чем элементов таким способом. 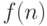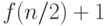Оценим сверху таким способом: после разбиения массива на два участка мы сначала сортируем более короткий (храня в стеке более длинный про запас), при этом глубина стека не больше , затем сортируем более длинный, так что