Рекурсия
7.4.8.
(Для знакомых с основами теории вероятностей). Доказать,
что математическое ожидание числа операций при работе этого
алгоритма не превосходит 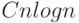 , причем константа
, причем константа  не зависит от сортируемого массива.
не зависит от сортируемого массива.
Указание.
Пусть 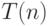 - максимум математического ожидания числа
операций для всех входов длины
- максимум математического ожидания числа
операций для всех входов длины  . Из текста процедуры
вытекает такое неравенство:
. Из текста процедуры
вытекает такое неравенство:
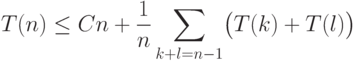
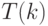 и
и 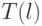 должны
стоять максимумы
должны
стоять максимумы 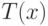 по всем
по всем  , не
превосходящим
, не
превосходящим  или
или  , но это не мешает дальнейшим рассуждениям.) Далее
индукцией по
, но это не мешает дальнейшим рассуждениям.) Далее
индукцией по  нужно доказывать оценку
нужно доказывать оценку 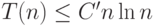 . При этом для вычисления среднего значения
. При этом для вычисления среднего значения 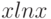 по
всем
по
всем 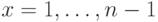 нужно вычислять
нужно вычислять 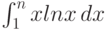 по частям как
по частям как 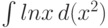 . При достаточно
большом
. При достаточно
большом  член
член  в правой части перевешивается за
счет интеграла
в правой части перевешивается за
счет интеграла 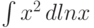 , и индуктивный шаг
проходит.
, и индуктивный шаг
проходит.7.4.9.
Имеется массив из  различных целых чисел
различных целых чисел ![{a[1]}\ldots{a[n]}](/sites/default/files/tex_cache/dce62e79eefc8a3d30d7b9890da6b90f.png) и число
и число  . Требуется найти
. Требуется найти  -ое по величине число
в этом массиве, сделав не более
-ое по величине число
в этом массиве, сделав не более  действий, где
действий, где  -
некоторая константа, не зависящая от
-
некоторая константа, не зависящая от  и
и  .
.
Замечание. Сортировка позволяет очевидным образом сделать
это за 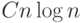 действий. Очевидный способ: найти
наименьший элемент, затем найти второй, затем
третий,
действий. Очевидный способ: найти
наименьший элемент, затем найти второй, затем
третий, 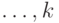 -ый требует порядка
-ый требует порядка 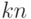 действий,
то есть не годится (константа при
действий,
то есть не годится (константа при  зависит от
зависит от  ).
).
Указание. Изящный (хотя практически и бесполезный - константы слишком велики) способ сделать это таков:
А. Разобьем наш массив на 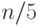 групп, в каждой из
которых по
групп, в каждой из
которых по 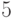 элементов. Каждую группу упорядочим.
элементов. Каждую группу упорядочим.
Б. Рассмотрим средние элементы всех групп и перепишем
их в массив из 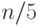 элементов. С помощью рекурсивного
вызова найдем средний по величине элемент этого массива.
элементов. С помощью рекурсивного
вызова найдем средний по величине элемент этого массива.
В. Сравним этот элемент со всеми элементами исходного
массива: они разделятся на большие его и меньшие его
(и один равный ему). Подсчитав количество тех и других, мы
узнаем, в какой из этих частей должен находится искомый
(  -ый) элемент и каков он там по порядку.
-ый) элемент и каков он там по порядку.
Г. Применим рекурсивно наш алгоритм к выбранной части.
Пусть 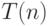 - максимально возможное число действий, если
этот способ применять к массивам из не более
чем
- максимально возможное число действий, если
этот способ применять к массивам из не более
чем  элементов (
элементов (  может быть каким угодно). Имеем
оценку:
может быть каким угодно). Имеем
оценку:

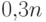 элементов. В самом
деле, если
элементов. В самом
деле, если  - средний из средних, то примерно половина
всех средних меньше
- средний из средних, то примерно половина
всех средних меньше  . А если в пятерке средний элемент
меньше
. А если в пятерке средний элемент
меньше  , то еще два заведомо меньше
, то еще два заведомо меньше  . Тем самым по
крайней мере
. Тем самым по
крайней мере 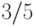 от половины элементов меньше
от половины элементов меньше  .
.Теперь по индукции можно доказать оценку 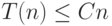 (решающую роль при этом играет то обстоятельство, что
(решающую роль при этом играет то обстоятельство, что 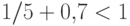 ).
).
