Свойства главных нумераций
Перечислимые свойства функций
Мы уже видели (теорема 21), что никакие (нетривиальные) свойства функций не являются разрешимыми. Но некоторые являются перечислимыми (в том смысле, что множество всех номеров всех функций, обладающих этим свойством, перечислимо). Например, таково свойство функции " быть где-то определенной" (см. выше). Другой пример: свойство " f(19) определено и равно 98 ".
Имеется довольно простое описание всех перечислимых свойств. Чтобы его сформулировать, нам потребуются некоторые определения.
Будем называть образцом функцию с натуральными
аргументами и значениями, имеющую конечную область определения.
Другими словами, образец есть конечный список пар 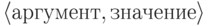 (в котором все
аргументы различны).
Образцы можно
рассматривать как конструктивные объекты (кодировать двоичными
словами, натуральными числами и т.п.). Это позволяет говорить о
разрешимом множестве образцов, перечислимом множестве образцов и т.п.
(в котором все
аргументы различны).
Образцы можно
рассматривать как конструктивные объекты (кодировать двоичными
словами, натуральными числами и т.п.). Это позволяет говорить о
разрешимом множестве образцов, перечислимом множестве образцов и т.п.
Каждому образцу t соответствует свойство функции "
продолжать этот образец ",
то есть множество 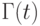 всех
(вычислимых) функций, которые являются продолжениями t.
(Заметим в скобках, что множества
всех
(вычислимых) функций, которые являются продолжениями t.
(Заметим в скобках, что множества 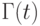 образуют базу
топологии на множестве всех вычислимых функций.) Легко
проверить, что для любого t и для любой вычислимой
нумерации U множество всех номеров всех функций
из
образуют базу
топологии на множестве всех вычислимых функций.) Легко
проверить, что для любого t и для любой вычислимой
нумерации U множество всех номеров всех функций
из 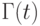 перечислимо.
В самом деле, надо параллельно вычислять значения Un(x) для
всех n и x ; как только накопленные данные позволяют
утверждать, что
перечислимо.
В самом деле, надо параллельно вычислять значения Un(x) для
всех n и x ; как только накопленные данные позволяют
утверждать, что  , надо
печатать n. (Если
, надо
печатать n. (Если  , то это обнаружится на конечном шаге, так как
область определения образца t конечна.)
, то это обнаружится на конечном шаге, так как
область определения образца t конечна.)
Пусть T произвольное множество образцов.
Через  обозначим множество всех вычислимых функций, которые продолжают
хотя бы один образец из T, то есть объединение
множеств
обозначим множество всех вычислимых функций, которые продолжают
хотя бы один образец из T, то есть объединение
множеств 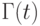 по всем
по всем 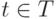 . Теперь мы можем сформулировать
обещанный результат:
. Теперь мы можем сформулировать
обещанный результат:
Теорема 24. (a) Пусть T произвольное перечислимое множество образцов, а U вычислимая универсальная функция для класса вычислимых функций одного аргумента. Тогда множество всех U -номеров всех функций из  перечислимо. (б) Пусть U главная универсальная функция (для класса
вычислимых функций одного аргумента). Пусть G
некоторое подмножество этого класса. Если множество
перечислимо. (б) Пусть U главная универсальная функция (для класса
вычислимых функций одного аргумента). Пусть G
некоторое подмножество этого класса. Если множество 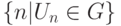 всех U -номеров всех функций из класса G перечислимо, то
всех U -номеров всех функций из класса G перечислимо, то 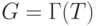 для
некоторого перечислимого множества образцов T.
для
некоторого перечислимого множества образцов T.
Например, упоминавшийся выше класс где-то определенных функций соответствует множеству всех непустых образцов (а также, скажем, множеству всех образцов с одноэлементной областью определения).
Часть (а) утверждения доказывается легко: надо параллельно вычислять все значения U(n,x) и перечислять все образцы из T ; как только обнаруживается, что какая-то из функций Un является продолжением какого-то образца из T, следует печатать n.
Содержательной является часть (б), где мы используем тот факт, что нумерация является главной. Нам понадобятся две леммы.
Лемма 1. Если вычислимая функция h является продолжением вычислимой функции g, принадлежащей классу G, то и функция h принадлежит классу G.
Лемма 2. Если вычислимая функция g принадлежит классу G, то существует функция h с конечной областью определения (образец), принадлежащая классу G, продолжением которой g является.
(Замечание в скобках. В совокупности эти две леммы утверждают, что любое перечислимое свойство G является открытым в описанной выше топологии.)
Покажем, как из этих лемм вытекает требуемое утверждение.
Заметим, что множество T всех образцов, принадлежащих
классу G, перечислимо. В самом деле, по
образцу как конструктивному объекту (т.е. по списку пар 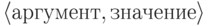 ) можно получить
его U -номер, поскольку функция U является главной.
(Формально: рассмотрим функцию
) можно получить
его U -номер, поскольку функция U является главной.
(Формально: рассмотрим функцию  и
применим определение главной универсальной функции.) Поэтому
множество T является перечислимым как прообраз перечислимого
множества всех U -номеров всех функций из
класса G.
и
применим определение главной универсальной функции.) Поэтому
множество T является перечислимым как прообраз перечислимого
множества всех U -номеров всех функций из
класса G.
Леммы 1 и 2 гарантируют, что 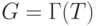 . В самом
деле, по лемме 1 любая функция из
. В самом
деле, по лемме 1 любая функция из  принадлежит
классу G, так как некоторая ее часть
принадлежит G. С другой стороны, лемма 2
гарантирует, что всякая функция g из G имеет
конечную часть, принадлежащую G (тем самым и T ) и
потому
принадлежит
классу G, так как некоторая ее часть
принадлежит G. С другой стороны, лемма 2
гарантирует, что всякая функция g из G имеет
конечную часть, принадлежащую G (тем самым и T ) и
потому  .
.
Осталось доказать леммы 1 и 2. Пусть, в противоречии с леммой 1, некоторая функция g принадлежит классу G, а ее продолжение h нет. Возьмем перечислимое неразрешимое множество K и рассмотрим такую функцию двух аргументов:
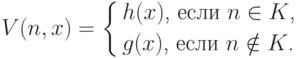
Эта функция вычислима. В самом деле, ее график, как легко проверить, перечислим как объединение графика g, умноженного на N, и графика h, умноженного на K. Другими словами, чтобы вычислить V(n,x), мы запускаем процесс перечисления K, а также (параллельно с этим процессом) вычисления g(x) и h(x). Результат выдается, если завершилось вычисление g(x) (в этом случае уже неважно, лежит ли n в K, так как h есть продолжение g ) или если завершилось вычисление h(x) и к тому же n обнаружилось в K.
Поскольку функция U является главной, существует всюду определенная функция s с таким свойством:
-
 ;
; -
 .
.
Тем самым дополнение к K является прообразом перечислимого множества номеров функций из G при вычислимом отображении s и потому (теорема 5) перечислимо. Полученное противоречие завершает доказательство леммы 1.
Лемма 2 доказывается аналогичным рассуждением. Пусть (вопреки утверждению леммы) функция g принадлежит классу G, но никакая ее конечная часть не принадлежит этому классу. Рассмотрим функцию
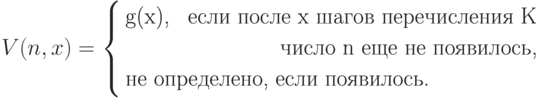
Легко видеть, что при 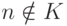 функция Vn
совпадает с g,
и потому принадлежит G, а при
функция Vn
совпадает с g,
и потому принадлежит G, а при 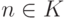 функция Vn
является конечной частью функции g и потому не
принадлежит G. Далее рассуждаем как в лемме 1.
функция Vn
является конечной частью функции g и потому не
принадлежит G. Далее рассуждаем как в лемме 1.
