Машинное обучение

2.3. Дерево решений

Идея, лежащая в основе алгоритма обучения дерева решений, состоит в рекурсивном разбиении пространства признаков с помощью простых правил на непересекающиеся области. Полученная в результате обучения модель представляет собой дерево, где каждому внутреннему узлу соответствует некоторая область пространства признаков и правило ее разбиения на подобласти (, если -й признак количественный и , если признак категориальный). Каждой листовой вершине также соответствует область пространства 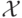и приписано константное значение, которому принимается равной функция в данной области.

Алгоритм обучения дерева решений, осуществления с его помощью предсказаний, сохранения/загрузки модели, а также дополнительный функционал по работе с деревьями решений реализованы в библиотеке OpenCV в классе CvDTree. Остановимся подробнее на описании данного класса.

Для обучения дерева решений служит метод train.

bool train( const Mat< trainData, 
            int tflag, 
            const Mat< responses, 
            const Mat< varIdx=Mat(), 
            const Mat< sampleIdx=Mat(), 
            const Mat< varType=Mat(), 
            const Mat< missingDataMask=Mat(), 
            CvDTreeParams params=CvDTreeParams() ); 
            

Рассмотрим параметры метода.

• trainData – матрица, содержащая векторы 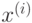из обучающей выборки. Матрица должна иметь тип CV_32F и размеры или . В отличие от метода CvSVM::train здесь возможен вариант как с построчным хранением векторов 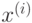, так и с их хранением по столбцам.
• tflag – флаг, определяющий по строкам (tflag=CV_ROW_SAMPLE) хранятся вектора выборки в матрице trainData или по столбцам (tflag=CV_COL_SAMPLE).
• responses – матрица-вектор, содержащая значения целевой переменной 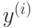для прецедентов обучающей выборки. Данная матрица должна иметь тип CV_32S или CV_32Fи размеры или .
• varIdx – матрица-вектор, содержащая либо номера признаков (тип матрицы CV_32S), которые необходимо использовать при обучении, либо маску (тип матрицы CV_8U) размера 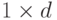, где единицами отмечены используемые признаки, нулями – игнорируемые. По умолчанию (varIdx=Mat()) используются все признаки.
• sampleIdx – матрица-вектор, имеющая такой же формат, как и varIdx, но отвечающая за прецеденты выборки, которые необходимо использовать для обучения. По умолчанию используются все имеющиеся прецеденты.
• varType – матрица-вектор, содержащая информацию о типах переменных. Деревья решений поддерживают использование как количественных (CV_VAR_ORDERED), так и категориальных (CV_VAR_CATEGORICAL) признаков. Данная матрица должна иметь тип CV_8U и размеры или , где последний элемент определяет тип целевой переменной. По умолчанию (varType=Mat()) целевая переменная считается категориальной, т.е. решается задача классификации, а остальные количественными.
• missingDataMask – матрица, содержащая маску пропущенных значений, где единицами отмечены неизвестные значения признаков, нулями – известные. В отличие от машины опорных векторов, деревья решений позволяют работать с пропущенными значениями в признаковых описаниях объектов 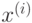. Матрица missingDataMask должна иметь тип CV_8U и по размеру совпадать с матрицей trainData. По умолчанию считается, что пропущенных значений нет.
• params – параметры алгоритма обучения.

Для представления параметров алгоритма обучения дерева решений используется структура CvDTreeParams:

struct CvDTreeParams 
{ 
    int   max_categories; 
    int   max_depth; 
    int   min_sample_count; 
    int   cv_folds; 
    bool  use_surrogates; 
    bool  use_1se_rule; 
    bool  truncate_pruned_tree; 
    float regression_accuracy; 
    const float* priors; 
 
    CvDTreeParams(); 
    CvDTreeParams( int max_depth, 
                   int min_sample_count, 
                   float regression_accuracy, 
                   bool use_surrogates, 
                   int max_categories, 
                   int cv_folds,                    bool use_1se_rule, 
                   bool truncate_pruned_tree, 
                   const float* priors ); 
}; 

Остановимся подробнее на описании данной структуры.

• max_depth – ограничение на высоту обучаемого дерева.
• min_sample_count – минимальное количество объектов обучающей выборки, которое должно быть в области пространства признаков, определяемой некоторым узлом дерева, чтобы разбиение этой области продолжилось.
• regression_accuracy – разбиение узла регрессионного дерева прекращается, если модуль разности значения, приписанного этому узлу, и истинного значения целевого признака для всех прецедентов, попавших в данный узел, не превышает данного значения.
• max_categories – максимальное количество возможных значений категориального признака, для которого точно вычисляется наилучшее правило разбиения. Данный параметр актуален лишь для задач классификации с числом классов больше двух, т.к. в данном случае выбор подмножества L множества возможных значений Q категориального признака происходит с помощью алгоритма с экспоненциальной от мощности Q трудоемкостью [2]. В данном случае для снижения времени работы алгоритма производится предварительная кластеризация множества Q так, чтобы количество кластеров не превышало max_categories. В случае если решается задача регрессии или бинарной классификации, то точное отыскания оптимального разбиения по данному признаку выполняется за линейное время от |Q| [2] и не требует предварительной кластеризации. Следует отметить, что максимальная поддерживаемая в OpenCV мощность равна 64.
• use_surrogates – флаг, определяющий необходимость построения суррогатных разбиений. Каждому узлу дерева решений может быть приписано не только одно (основное) правило разбиения, а также несколько второстепенных (суррогатных) правил. В качестве суррогатных выбираются разбиения наиболее похожие на основное [1]. Построение суррогатных разбиений (use_surrogates=true) ведет к росту времени обучения модели, однако, может повысить качество оценки значимости переменных с помощью построенного дерева и улучшить качество предсказания для объектов с пропущенными значениями.
• cv_folds – количество частей, на которые разделяется обучающая выборка, для выполнения перекрестного контроля при выполнении процедуры отсечений (pruning) [1]. Типичная стратегия построения дерева решений заключается в обучении большого дерева, к которому затем применяются отсечения для предотвращения переобучения. Если cv_folds=0, то отсечения не выполняются.
• use_1se_rule – использование более строгого критерия отсечения. Если use_1se_rule=true, то после процедуры отсечения получается меньшее дерево.
• truncate_pruned_tree – указывает, следует ли физически удалять из памяти отсеченные узлы дерева.
• priors – для задачи классификации, задает априорные вероятности появления точек различных классов. Данный параметр можно использовать, например, в случае несбалансированной обучающей выборки, т.е. неравного количества прецедентов разных классов.

Предсказания с помощью предварительно обученной модели выполняются с помощью метода predict:

CvDTreeNode* predict( const Mat< sample, 
                      const Mat< missingDataMask=Mat(), 
                      bool preprocessedInput=false ) const; 
                      

Рассмотрим параметры данного метода:

• sample – матрица-вектор типа CV_32F и размера 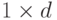, содержащая координаты одной точки в пространстве признаков.
• missingDataMask – матрица-вектор типа CV_8U и размера 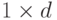, представляющая собой маску пропущенных значений в sample.
• preprocessedInput – определяет порядок работы с категориальными признаками в ходе предсказания. В матрице признаковых описаний объектов обучающей выборки, используемой методом CvDTree::train, значения категориальных признаков могут быть обозначены произвольными целыми числами. Например, множеством различных значений признака может быть {3,7,9}. Однако внутренним представлением обученной модели является множество, состоящее из чисел от 0 до . Таким образом, на этапе предсказания требуется выполнять пересчет значений категориальных признаков, что может негативно сказаться на скорости выполнения данной операции. Значение preprocessedInput=true говорит, что пересчет значений уже выполнен. Данный параметр актуален лишь при наличии категориальных признаков.

Следует отметить, что метод CvDTree::predict возвращает указатель на структуру, описывающую узел дерева. Само предсказанное моделью значение целевого признака хранится в поле value данной структуры.

Сохранение модели дерева решений в файл и загрузка из него выполняется с помощью методов save и load, использование которых полностью совпадает с аналогичными методами класса CvSVM, описанными выше.

Следует отметить, что класс CvDTree также содержит дополнительный функционал, например, для определения значимости различных переменных для восстановления зависимости от , что, однако, выходит за рамки данной лабораторной работы и может быть предоставлено для самостоятельного изучения [7].

Приведем пример использования класса CvDTree для решения задачи бинарной классификации аналогичной, решаемой в примере для CvSVM.

#include <stdlib.h> 
#include <stdio.h> 
#include <opencv2/core/core.hpp> 
#include <opencv2/ml/ml.hpp> 
 
using namespace cv; 
 
// размерность пространства признаков 
const int d = 2; 
 
// функция истинной зависимости целевого признака 
// от остальных 
int f(Mat sample) 
{ 
    return (int)((sample.at<float>(0) < 0.5f && 
                  sample.at<float>(1) < 0.5f) || 
                 (sample.at<float>(0) > 0.5f && 
                  sample.at<float>(1) > 0.5f)); 
} 
 
int main(int argc, char* argv[]) 
{ 
    // объем генерируемой выборки 
    int n = 2000; 
    // объем обучающей части выборки 
    int n1 = 1000; 
     
    // матрица признаковых описаний объектов 
    Mat samples(n, d, CV_32F); 
    // номера классов (матрица значений целевой переменной)     Mat labels(n, 1, CV_32S); 
    // генерируем случайным образом точки 
    // в пространстве признаков 
    randu(samples, 0.0f, 1.0f); 
 
    // вычисляем истинные значения целевой переменной 
    for (int i = 0; i < n; ++i) 
    { 
        labels.at<int>(i) = f(samples.row(i)); 
    } 
 
    // создаем маску прецедентов, которые будут 
    // использоваться для обучения: используем n1 
    // первых прецедентов 
    Mat trainSampleMask(1, n1, CV_32S); 
    for (int i = 0; i < n1; ++i) 
    { 
        trainSampleMask.at<int>(i) = i; 
    } 
 
    // будем обучать дерево решений высоты не больше 10, 
    // после построения которого выполним отсечения 
    // с помощью пятикратного перекресного контроля 
    CvDTreeParams params; 
    params.max_depth = 10; 
    params.min_sample_count = 1; 
    params.cv_folds = 5; 
 
    CvDTree dtree; 
    Mat varIdx(1, d, CV_8U, Scalar(1)); 
    Mat varTypes(1, d + 1, CV_8U, Scalar(CV_VAR_ORDERED)); 
    varTypes.at<uchar>(d) = CV_VAR_CATEGORICAL; 
    dtree.train(samples, CV_ROW_SAMPLE, 
                labels, varIdx, 
                trainSampleMask, varTypes, 
                Mat(), params); 
    dtree.save("model-dtree.yml", "simpleDTreeModel"); 
     
    // вычисляем ошибку на обучающей выборке 
    float trainError = 0.0f; 
    for (int i = 0; i < n1; ++i) 
    { 
        int prediction = 
            (int)(dtree.predict(samples.row(i))->value); 
        trainError += (labels.at<int>(i) != prediction); 
    } 
    trainError /= float(n1); 
 
    // вычисляем ошибку на тестовой выборке 
    float testError = 0.0f;     for (int i = 0; i < n - n1; ++i) 
    { 
        int prediction =  
          (int)(dtree.predict(samples.row(n1 + i))->value); 
        testError += 
            (labels.at<int>(n1 + i) != prediction); 
    } 
    testError /= float(n - n1); 
 
    printf("train error = %.4f\ntest error = %.4f\n", 
           trainError, testError); 
     
    return 0; 
} 

Иллюстрацией разбиения пространства признаков обученным с помощью данного кода деревом решений служит рис. 10.2.

Рис. 10.2. Точки обучающей выборки и разбиение пространства признаков деревом решений