|
Нахожу в тесте вопросы, которые в принципе не освещаются в лекции. Нужно гуглить на других ресурсах, чтобы решить тест, или же он всё же должен испытывать знания, полученные в ходе лекции? |
Машинное обучение
2. Обзор возможностей библиотеки OpenCV для решения задач обучения с учителем
2.1. Задача обучения с учителем
Одной из задач, изучаемой в машинном обучении, является задача
обучения с учителем, которая заключается в как можно более точном
восстановлении (определении) вида зависимости 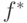 некоторой величины
некоторой величины
 , от вектора
, от вектора  по конечному набору пар (прецедентов)
по конечному набору пар (прецедентов)
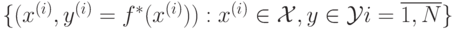 , называемому
обучающей выборкой. Множество
, называемому
обучающей выборкой. Множество 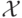 называется пространством признаков,
компоненты вектора
называется пространством признаков,
компоненты вектора  , в свою очередь, признаками, y – целевым
признаком или выходом. В рамках данной лабораторной работы будет
рассматриваться конечное и неупорядоченное множество
, в свою очередь, признаками, y – целевым
признаком или выходом. В рамках данной лабораторной работы будет
рассматриваться конечное и неупорядоченное множество 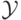 (далее будем
предполагать, что
(далее будем
предполагать, что 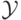 состоит из целых чисел, не используя никакие
отношения порядка), т.е. решать задачу классификации. Также в качестве
множества
состоит из целых чисел, не используя никакие
отношения порядка), т.е. решать задачу классификации. Также в качестве
множества 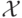 будем рассматривать d-мерное вещественное пространство
будем рассматривать d-мерное вещественное пространство
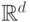 .
.
Алгоритмы, решающие задачу обучения с учителем, выполняют поиск
функции (модели) из некоторого фиксированного множества
из некоторого фиксированного множества  ,
зависящего от конкретного алгоритма. Процесс выбора функции
,
зависящего от конкретного алгоритма. Процесс выбора функции  называется обучением.
называется обучением.
Для оценки качества построенной модели зависимости от используется множество прецедентов, не использовавшихся на этапе обучения, на котором вычисляется некоторый функционал качества (для задачи классификации, зачастую, рассматривается доля неверно классифицированных прецедентов).
Модуль ML библиотеки OpenCV содержит реализации следующих алгоритмов обучения с учителем: нормальный байесов классификатор, метод k ближайших соседей, нейронная сеть, машина опорных векторов, дерево решений, различные алгоритмы бустинга деревьев решений, в том числе градиентный бустинг, случайный лес и крайне случайный лес [1]. Каждый алгоритм обладает своими достоинствами и недостатками. Различные алгоритмы имеют свои ограничения применимости, например, могут быть предназначены только для задач классификации/восстановления регрессии, могут допускать работу лишь с количественными признаками, могут не поддерживать наличие пропущенных значений, т.е. неизвестных значений некоторых признаков у какого-либо прецедента. Также, тип функции, получаемой на выходе определенного алгоритма обучения, может лучше/хуже подходить для аппроксимации искомой зависимости. Таким образом, конкретный алгоритм обучения с учителем должен выбираться, исходя из специфики конкретной рассматриваемой задачи. Данная лабораторная работа посвящена описанию использования реализаций следующих алгоритмов: машина опорных векторов, дерево решений, случайный лес и градиентный бустинг деревьев решений.
2.2. Машина опорных векторов
Пусть  , т.е. рассматривается задача бинарной классификации.
Идея алгоритма машины опорных векторов (Support Vector Machine, SVM)
заключается в построении оптимальной поверхности
, т.е. рассматривается задача бинарной классификации.
Идея алгоритма машины опорных векторов (Support Vector Machine, SVM)
заключается в построении оптимальной поверхности  ,
представляющей собой гиперплоскость в спрямляющем пространстве
,
представляющей собой гиперплоскость в спрямляющем пространстве
 (см. лекционную часть курса), разделяющей точки
(см. лекционную часть курса), разделяющей точки  различных классов из обучающей выборки. Фактически, обучение
алгоритмом опорных векторов заключается в решении оптимизационной
задачи
различных классов из обучающей выборки. Фактически, обучение
алгоритмом опорных векторов заключается в решении оптимизационной
задачи

при ограничениях
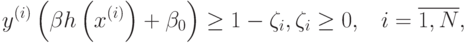
где отображение 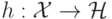 задает переход в спрямляющее пространство,
задает переход в спрямляющее пространство,
 – параметр алгоритма обучения, регулирующий величину штрафа за
то, что некоторые точки выходят за границу разделяющей полосы
– параметр алгоритма обучения, регулирующий величину штрафа за
то, что некоторые точки выходят за границу разделяющей полосы
 . При этом отображение h может быть задано неявно с
помощью, так называемого, ядра
. При этом отображение h может быть задано неявно с
помощью, так называемого, ядра 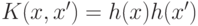 Решающая функция
запишется в виде
Решающая функция
запишется в виде  . Данная функция зависит от некоторых точек
. Данная функция зависит от некоторых точек 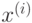 из обучающей
выборки, называемых опорными векторами.
из обучающей
выборки, называемых опорными векторами.
Данный метод применим для решения задач классификации, но также может быть обобщен на случай регрессии [1], однако, подробное изложение регрессионного алгоритма выходит за рамки данной лабораторной работы. Также, несмотря на то, что выше описывался алгоритм бинарной классификации с использованием машины опорных векторов, данный метод легко обобщается на случай произвольного количества классов с помощью универсальных подходов "один против всех" или "каждый против каждого", тем самым сводясь к решению нескольких задач классификации с двумя классами. Машина опорных векторов как для классификации, так и для восстановления регрессии работает лишь с количественными признаками и не допускает наличия пропущенных значений.
Функционал, связанный с обучением машины опорных векторов, ее сохранением/загрузкой и использованием обученной модели для осуществления предсказаний реализован в классе CvSVM, как и все реализации алгоритмов обучения с учителем в библиотеке, унаследованном от класса CvStatModel. Остановимся подробнее на описании данного класса.
Для обучения машины опорных векторов служит метод train.
bool CvSVM::train(const Mat< trainData,
const Mat< responses,
const Mat< varIdx=Mat(),
const Mat< sampleIdx=Mat(),
CvSVMParams params=CvSVMParams());
Параметры:
-
trainData – матрица, содержащая векторы
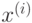 из обучающей
выборки. Матрица должна иметь тип CV_32F и размеры
из обучающей
выборки. Матрица должна иметь тип CV_32F и размеры  ,
таким образом, храня в i-й строке координаты вектора
,
таким образом, храня в i-й строке координаты вектора 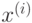 .
. -
responses – матрица-вектор, содержащая значения целевой
переменной
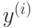 для прецедентов обучающей выборки. Данная
матрица должна иметь тип CV_32S или CV_32F и размеры
для прецедентов обучающей выборки. Данная
матрица должна иметь тип CV_32S или CV_32F и размеры  или
или  .
. -
varIdx – матрица-вектор, содержащая либо номера признаков
(тип матрицы CV_32S), которые необходимо использовать при
обучении, либо маску (тип матрицы CV_8U) размера
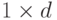 , где
единицами отмечены используемые признаки, нулями –
игнорируемые. По умолчанию (varIdx=Mat()) используются все
признаки.
, где
единицами отмечены используемые признаки, нулями –
игнорируемые. По умолчанию (varIdx=Mat()) используются все
признаки. - sampleIdx – матрица-вектор, имеющая такой же формат, как и varIdx, но отвечающая за прецеденты выборки, которые необходимо использовать для обучения. По умолчанию используются все имеющиеся прецеденты.
- params – параметры алгоритма обучения.
Для представления параметров SVM в OpenCV используется структура CvSVMParams.
struct CvSVMParams
{ CvSVMParams();
CvSVMParams( int svm_type,
int kernel_type,
double degree,
double gamma,
double coef0,
double Cvalue,
double nu,
double p,
CvMat* class_weights,
CvTermCriteria term_crit );
int svm_type;
int kernel_type;
double degree;
double gamma;
double coef0;
double C;
double nu;
double p;
CvMat* class_weights;
CvTermCriteria term_crit;
};
Рассмотрим поля данной структуры.
Поле svm_type отвечает за тип используемой машины опорных векторов. Возможные значения данной переменной описаны перечислением в классе CvSVM:
enum {C_SVC=100, NU_SVC=101, ONE_CLASS=102, EPS_SVR=103,
NU_SVR=104};
C_SVC и NU_SVC обозначают различные модификации SVM для
классификации, в то время как EPS_SVR и NU_SVR представляют собой
формализации для регрессии. Машина опорных векторов типа ONE_CLASS
строит границу области, в которой расположены точки одного
единственного класса. Описанная выше задача оптимизации соответствует
типу C_SVC (формализации с использованием параметра C). SVM типа
NU_SVC решает схожую, но другую задачу с параметром ![v \in [0,1]](/sites/default/files/tex_cache/7eeac3bdac96def7b99bf96a57424fdc.png) - ,
являющимся нижней оценкой на долю опорных векторов в обучающей
выборке и верхней границей доли неправильно классифицированных
прецедентов обучающей выборки.
- ,
являющимся нижней оценкой на долю опорных векторов в обучающей
выборке и верхней границей доли неправильно классифицированных
прецедентов обучающей выборки.
Поле kernel_type структуры CvSVMParams служит для обозначения используемого ядра. Возможные значения данной переменной также описаны в перечислении класса CvSVM:
enum { LINEAR=0, POLY=1, RBF=2, SIGMOID=3 };
В библиотеке OpenCV реализована непосредственная поддержка следующих ядер:
- линейное ядро (LINEAR):
 ;
; - многочлен степени d (POLY):
 ;
; - радиальная функция (RBF):
 ;
; - сигмоидальная функция (SIGMOID):
 .
.
Далее в структуре CvSVMParams идут параметры ядер: degree соответствует степени многочлена, определяющего полиномиальное ядро, gamma – параметру в полиномиальном, радиальном и сигмоидальном ядрах, coef0 – параметру в полиномиальном и сигмоидальном ядрах. При использовании ядра, не имеющего того или иного параметра, значение, хранящееся в соответствующем поле структуры, игнорируется и может быть любым.
Поля C, nu и p соответствуют параметрам оптимизационных задач, решаемых алгоритмом обучения. Тип используемой машины опорных векторов указывает на то, какой из этих параметров "активен": C используется совместно с C_SVC, EPS_SVR и NU_SVR; nu – с NU_SVC, NU_SVR и ONE_CLASS; p – с EPS_SVR.
Поле class_weights предназначено для хранения матрицы-вектора, содержащей веса различных классов и может использоваться с машиной опорных векторов типа C_SVC, позволяя определить различные значения параметра для точек разных классов. Как отмечалось выше, решение задачи классификации более чем на два класса сводится к серии задач бинарной классификации. В CvSVM реализован подход "каждый против каждого". Таким образом, при решении задачи разделения точек классов
![\min_{\beta,\beta_{0},\zeta}\frac{1}{2}\parallel \beta\parallel + class\_weights[k_{1}] \cdot C \sum_{i:y_{i}=k_{1}} \zeta_{i} + class\_weights[k_{2}] \cdot C \sum_{i:y_{i}=k_{2}} \zeta_{i}.](/sites/default/files/tex_cache/a306af4ed1542c46d7e69bebd5e249d0.png)
Данный параметр может быть полезен при несбалансированной обучающей выборке, содержащей малое количество прецедентов одного класса и большое количество другого. Чем больше вес, тем больший штраф назначается за неправильную классификацию обучающего прецедента этого класса. По умолчанию (class_weights = NULL) все веса равны.

 "
"