|
Здравствуйие! Я хочу пройти курс Введение в принципы функционирования и применения современных мультиядерных архитектур (на примере Intel Xeon Phi), в презентации самостоятельной работы №1 указаны логин и пароль для доступ на кластер и выполнения самостоятельных работ, но войти по такой паре логин-пароль не получается. Как предполагается выполнение самосоятельных работ в этом курсе? |
Самостоятельная работа 5: Оптимизация вычислений в задаче матричного умножения. Оптимизация работы с памятью
Применение Intel MKL для умножения плотных матриц
В C/C++ для умножения матриц с использованием Intel MKL необходимо использовать функцию BLAS третьего уровня – ?gemmте вопросительного знака в имени функции применяется символ, идентифицирующий используемый тип данных. Так, для типа float используется символ "s". Функция позволяет вычислять выражения:
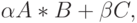
 и
и  – вещественные коэффициенты.
– вещественные коэффициенты.
Далее представлен пример вызова функции:
cblas_sgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans,
m, n, k, alpha, A, k, B, n, beta, C, n);
Рассмотрим значение параметров вызова.
- Значение CblasRowMajor показывает, что матрица хранится по строкам.
- Значение CblasNoTrans сообщает, что исходные матрицы A и B не транспонированы.
- Переменные m, n и k задают размеры исходных матриц:
- A: m строк и k столбцов.
- B: k строк и n столбцов.
- C: m строк и n столбцов.
- Переменные alpha и beta – коэффициенты, используемые в формуле.
- A, B – массивы, содержащие исходные матрицы.
- С – результат вычислений.
Более подробную информацию о параметрах можно получить в официальной документации по Intel MKL [12.5].
Разделим реализацию алгоритма умножения матриц на несколько файлов. В начале, объявим определение вещественного типа данных и ряд прототипов функций:
// routine.h
#ifndef _ROUTINE_H
#define _ROUTINE_H
#ifndef ELEMENT_TYPE
#define ELEMENT_TYPE float
#endif
// выделение памяти для хранения матриц
void allocMatrix(ELEMENT_TYPE ** mat, int n);
// освобождение памяти
void freeMatrix (ELEMENT_TYPE ** mat);
// генерация элементов матрицы
void genMatrix(ELEMENT_TYPE * mat, int n);
// определение ошибки вычислений
ELEMENT_TYPE calculationError(ELEMENT_TYPE * A,
ELEMENT_TYPE * B, ELEMENT_TYPE * C, int n);
#endif
Реализацию функций выделения/освобождения памяти и генерации плотных матриц читателю предлагается реализовать самостоятельно. Для определения корректности разработанных нами программ в дальнейшем предлагается сравнивать результат с результатом работы функции умножения матриц, предоставляемой в Intel MKL. Реализовать подобную функцию также предлагается самостоятельно.
Создадим заголовочный файл с прототипом функции умножения матриц:
// mult.h
#ifndef _MULT_
#define _MULT_
#include "routine.h"
//умножение матриц
void mult(ELEMENT_TYPE * A, ELEMENT_TYPE * B,
ELEMENT_TYPE * C, int n);
#endif
Реализуем функцию умножения с использованием MKL:
// MKL.cpp
#include "mult.h"
#include "mkl.h"
void mult(ELEMENT_TYPE * A, ELEMENT_TYPE * B,
ELEMENT_TYPE * C, int n)
{
ELEMENT_TYPE alpha, beta;
alpha = 1.0;
beta = 0.0;
cblas_sgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans,
n, n, n, alpha, A, n, B, n, beta, C, n);
}
Подготовим функцию main():
// main.cpp
#include <stdio.h>
#include "omp.h"
#include "mult.h"
int testThreadCount();
int main(int argc, char **argv)
{
double time_s, time_f;
int th;
int n = 0;
// чтение размера матиц
if(argc < 2)
{
printf("<exec> <n>");
return -1;
}
n = atoi(argv[1]);
// вывод количества потоков
th = testThreadCount();
printf("Intel Xeon Phi threads number: %d \n\n", th);
ELEMENT_TYPE *A, *B, *C;
// выделение памяти
allocMatrix(&A, n);
allocMatrix(&B, n);
allocMatrix(&C, n);
// генерация матриц A и B
genMatrix(A, n);
genMatrix(B, n);
// умножение матриц
time_s = omp_get_wtime( );
mult(A, B, C, n);
time_f = omp_get_wtime( );
printf( "Size of matrix : %d \n", n);
printf( "Calculation time : %3.3f \n",
(time_f - time_s));
// проверка корректности реализованного алгоритма
#ifndef NO_DEBUG
double err;
err = calculationError(A, B, C, n);
printf( "Calculation error : %3.5f \n", err);
#endif
// освобождение памяти
freeMatrix(&A);
freeMatrix(&B);
freeMatrix(&C);
return 0;
}
// функция, определяющая количество потоков
int testThreadCount() {
int thread_count;
#pragma omp parallel
{
#pragma omp single
thread_count = omp_get_num_threads();
}
return thread_count;
}
Для компиляции кода с использованием многопоточной версии Intel MKL, можно использовать следующую строку:
icpc –mkl=parallel -openmp ./MKL.cpp ./main.cpp ./routine.cpp –oMKL
Если необходимо скомпилировать код, гарантируя использование последовательных версий алгоритмов из Intel MKL, строка компиляции незначительно меняется:
icpc –mkl=sequential -openmp ./MKL.cpp ./main.cpp ./routine.cpp –oMKL
Запустить полученный код можно строкой следующего вида:
./MKL 3072
Для компиляции программ, исполняемых на сопроцессоре Intel Xeon Phi, необходимо в строку компиляции добавить еще один ключ компилятора (-mmic):
icpc -mmic –mkl=parallel -openmp ./MKL.cpp ./main.cpp ./routine.cpp –oMKL
Для запуска кода можно зайти на сопроцессор, используя ssh:
ssh mic0 ./MKL 3072
Запустим полученный код. На рис. 10.1 представлен результат запуска разработанной программы на сопроцессоре Intel Xeon Phi.
увеличить изображение
Рис. 10.1. Пример запуска программы на сопроцессоре Intel Xeon Phi с использованием Intel MKL
В таблице 10.2 представлены результаты запуска умножения матриц на хосте и на сопроцессоре в последовательном и параллельном режиме при разных размерах матрицы. Для замера времени здесь и далее проводилась серия экспериментов, в качестве времени выполнения бралось минимальное время работы программы.
| MKL sequential | MKL parallel | |||
| N | Intel Xeon | Intel Xeon Phi | Intel Xeon | Intel Xeon Phi |
| 1024 | 0,128 | 0,207 | 0,031 | 0,110 |
| 2048 | 0,337 | 1,363 | 0,055 | 0,140 |
| 3048 | 1,059 | 4,411 | 0,193 | 0,244 |
Сравним время работы на хосте и на сопроцессоре. Время работы на одном ядре CPU ожидаемо лучше, чем время работы на одном ядре Xeon Phi. Как неоднократно говорилось в лекциях по архитектуре, ядра сопроцессора существенно слабее ядер CPU. Да, конечно, их намного больше, но ведь в последовательных запусках мы это никак не используем!
Обратим внимание на параллельные запуски. Здесь мы ожидаем, что MKL на сопроцессоре покажет лучший результат, чем MKL на 16 ядрах CPU. Тем не менее, этого не происходит. Попробуем разобраться с этим фактом. Вспомним результаты, полученные нами в предыдущей лабораторной работе. Там нами было выяснено, что так называемый "прогрев" (warm up) оказывает существенное влияние на время работы программы, использующей MKL (а иногда и не только), особенно на сопроцессоре. Причин тому несколько: накладные расходы на создание потоков, настройка TLB-кеша, особенности внутреннего устройства MKL (достоверно подтвердить или опровергнуть этот факт мы не можем) и др1Те, кто не очень верят в "шаманство" с прогревом или считают это каким-то жульничест-вом, могут провести следующий эксперимент. Создаем программу, в которой запускаем sgemm, выполняющий C=D*E. Далее той же программе в цикле, скажем, 10 раз запускаем sgemm, выполняющий C=A*B. Авторы обнаружили, что первый sgemm(D, E) работает зна-чител ьно дольше, чем первый из sgemm(A, B), который, в свою очередь, несколько быстрее, чем следующий sgemm(A, B). Далее время стабилизируется. Эти результаты позволяют сделать предположения о том, какие из эффектов прогрева оказывают влияние на время работы и в какой момент это происходит. . В той же работе обсуждался вопрос о корректности использования прогрева и доверия соответствующим результатам. Забегая вперед, скажем, что для всех последующих наших реализаций прогрев при существенных размерах матриц не оказывает значимого воздействия на время работы, поэтому мы будем приводить результаты, не уточняя, использовался прогрев или нет. В то же время, для MKL наличие прогрева существенно влияет на время работы. Учитывая, что современные программы обычно делают что-то более значимое, чем однократное умножение двух матриц, будем анализировать результаты MKL, полученные с использованием прогрева – в оптимальной для библиотеки конфигурации.
| MKL sequential | MKL parallel | MKL parallel + warm up | ||||
| N | Intel Xeon | Intel Xeon Phi | Intel Xeon | Intel Xeon Phi | Intel Xeon | Intel Xeon Phi |
| 1024 | 0,128 | 0,207 | 0,031 | 0,110 | 0,012 | 0,004 |
| 2048 | 0,337 | 1,363 | 0,055 | 0,140 | 0,047 | 0,019 |
| 3048 | 1,059 | 4,411 | 0,193 | 0,244 | 0,129 | 0,062 |
| 10000 | 35,198 | 130,983 | 4,05 | 2,06 | 2,765 | 1,835 |
Перестроим таблицу (таблице 10.3), добавив результаты с прогревом и для N = 10000. Здесь мы видим, что прогрев сокращает время работы как на CPU, так и на Xeon Phi, при этом сопроцессор начинает обгонять 16 ядер CPU.
В дальнейшем все эксперименты будут проводиться на сопроцессоре Intel Xeon Phi.

