|
Здравствуйие! Я хочу пройти курс Введение в принципы функционирования и применения современных мультиядерных архитектур (на примере Intel Xeon Phi), в презентации самостоятельной работы №1 указаны логин и пароль для доступ на кластер и выполнения самостоятельных работ, но войти по такой паре логин-пароль не получается. Как предполагается выполнение самосоятельных работ в этом курсе? |
Самостоятельная работа 5: Оптимизация вычислений в задаче матричного умножения. Оптимизация работы с памятью
Введение
Презентацию к лабораторной работе Вы можете скачать здесь.
С одной стороны, программирование для Intel Xeon Phi по своей сути мало чем отличается от программирования для традиционных центральных процессоров. Как и раньше, мы должны эффективно использовать векторные наборы команд (парадигма SIMD, параллелизм по данным), обеспечивать по возможности равномерную загрузку потоков (параллелизм на уровне ядер), эффективно работать с памятью (учет многоуровневой схемы организации памяти).
Методы достижения цели также являются в определенной степени стандартными. Так, для векторизации вычислений мы можем использовать высокопроизводительные библиотеки, возможности оптимизирующих компиляторов, помогая им специальными опциями и директивами, применять технологию Intel Cilk Plus, при необходимости реализовывать некоторые части программы с использованием интринсиков или ассемблерных вставок. При этом более широкие регистры, наличие FMA, расширенные операции для работы с памятью и некоторые другие особенности векторных расширений в системе команд Xeon Phi способны значительно ускорить расчеты. Для достижения параллелизма на уровне ядер мы можем использовать хорошо знакомые технологии (MPI, OpenMP, Intel Cilk Plus и др.). При этом выбор подходящего сочетания числа процессов и потоков может оказывать существенное влияние на итоговую производительность программы. Базовые методы оптимизации работы с памятью также являются достаточно стандартными. Так, мы должны заботиться об эффективном использовании кеш-памяти, стараться избегать перегрузки шины данных, а также минимизировать обмены с оперативной памятью хоста. В целом, оптимизация на традиционных процессорах Intel часто приводит к сокращению времени работы на Xeon Phi и наоборот. Тем не менее, это не одно и то же. В лекциях и лабораторных работах данного курса на примерах демонстрируется, как меняется время работы на хосте и на сопроцессоре в результате применения различных техник оптимизации.
Основная идея данной работы заключается в изучении базовых принципов применения перечисленных выше способов повышения производительности на примере известной, широко распространенной в приложениях и хорошо исследованной в литературе задачи – умножении плотных матриц. В отличие от предыдущих лабораторных работ, подробно изучающих разные техники оптимизации расчетов, основное внимание уделяется вопросам оптимизации работы с памятью.
Методические указания
Цели и задачи работы
Цель данной лабораторной работы – рассмотрение вопросов оптимизации работы с памятью при разработке программ для Intel Xeon Phi. Основное внимание уделяется базовым методам повышения эффективности использования кеш-памяти. В качестве примера используется задача умножения квадратных плотных матриц. Считается, что все данные, участвующие в расчетах, целиком помещаются в оперативную память.
Данная цель предполагает решение следующих основных задач:
- Использование библиотеки Intel MKL для решения задачи умножения матриц на хосте и на сопроцессоре.
- Последовательная реализация алгоритма умножения матриц по определению.
- Изучение вопроса о производительности базовой версии, рассмотрение способов сокращения времени вычислений с использованием векторизации, выбор подходящего порядка обращения к данным.
- Реализация последовательной и параллельной версий блочного алгоритма для умножения матриц.
Структура работы
Рассматривается задача умножения плотных матриц. Для сравнения результатов вычислений и времени работы реализуется умножение плотных матриц с использованием высокопроизводительной библиотеки Intel MKL. Приводится наивная реализация алгоритма умножения матриц. Рассматриваются вопросы влияния порядка циклов на время вычислений на сопроцессор Intel Xeon Phi. Изучается влияние выравнивания и подсказок компилятору на векторизацию вычислений. Реализуется несколько редакций блочного алгоритма умножения матриц. Формулируются задания для самостоятельной проработки.
Тестовая инфраструктура
Для проведения экспериментов использовались вычислительные ресурсы МСЦ РАН (МВС-10П) [12.3]. Тестовая инфраструктура представлена в таблице 10.1.
| Процессор | 2 процессора на узел Xeon E5-2690 (2.9 GHz, 8 ядер) |
| Память | 64 GB |
| Сопроцессор | Intel Xeon Phi 7110X |
| Операционная система | Linux CentOS 6.2 |
| Компилятор, профилировщик, отладчик | Intel C/C++ Compiler 14 |
Задача умножения плотных матриц
Пусть даны две матрицы A и B размерности  . По определению результатом умножения двух матриц является матрица C размерности
. По определению результатом умножения двух матриц является матрица C размерности  , где каждый элемент матрицы вычисляется по формуле:
, где каждый элемент матрицы вычисляется по формуле:
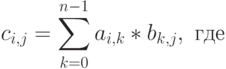

Этот алгоритм предполагает выполнение 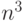 операций умножения и
операций умножения и 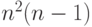 операций сложения элементов исходных матриц
операций сложения элементов исходных матриц  операций.
операций.
Известны последовательные алгоритмы умножения матриц, обладающие меньшей вычислительной сложностью. В частности, к таким алгоритмам относится алгоритм Штрассена. В данном алгоритме каждое восьмое умножение заменяется сложениями, что приводит к оценке сложности 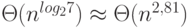 . Еще меньшей оценкой сложности обладает алгоритм Копперсмита-Винограда
. Еще меньшей оценкой сложности обладает алгоритм Копперсмита-Винограда  . Данный алгоритм был улучшен в 2010 году Вирджинией Вильямс. Сложность алгоритма составила
. Данный алгоритм был улучшен в 2010 году Вирджинией Вильямс. Сложность алгоритма составила  . Ряд исследователей считают, что данную оценку можно существенно улучшить. Желающие ознакомиться с теоретическими аспектами данной проблемы могут, например, изучить обзор алгоритмов в диссертации Вирджинии Вильямс (http://theory.stanford.edu/~virgi/thesis.pdf) и ряд публикаций, свободно доступных с ее персональной страницы (http://theory.stanford.edu/~virgi).
. Ряд исследователей считают, что данную оценку можно существенно улучшить. Желающие ознакомиться с теоретическими аспектами данной проблемы могут, например, изучить обзор алгоритмов в диссертации Вирджинии Вильямс (http://theory.stanford.edu/~virgi/thesis.pdf) и ряд публикаций, свободно доступных с ее персональной страницы (http://theory.stanford.edu/~virgi).
Несмотря на существование более совершенных алгоритмов с точки зрения асимптотики, на практике их применяют редко. Как правило, в оценке сложности присутствует большая константа. Как следствие, алгоритмы обладают лучшей производительностью только при слишком больших размерах матриц, не помещающихся в оперативную память современных компьютеров.
В рамках лабораторной работы для демонстрации подходов к реализации и последующей оптимизации алгоритма умножения матриц на сопроцессоре Intel Xeon Phi будем использовать алгоритм, получаемый из определения. Будем считать, что матрицы хранят данные с плавающей запятой в одинарной точности.
