Самостоятельная работа 4: Оптимизация расчетов на примере задачи вычисления справедливой цены опциона Европейского типа

Понятие опциона и справедливой цены

Опцион – производный финансовый инструмент – контракт между сторонами и , который дает право стороне в некоторый момент времени в будущем купить у стороны или продать стороне акции по цене K, зафиксированной в контракте. За это право сторона выплачивает фиксированную сумму (премию) C стороне . При этом называется ценой исполнения опциона (страйк, strike price), а C – ценой опциона.

В данной работе рассматривается простейший вариант опциона – колл-опцион европейского типа на акцию. Основная идея заключения контракта состоит в игре двух лиц – и . Вторая сторона выплачивает некоторую сумму C и в некоторый момент времени (срок выплаты, maturity, зафиксирован в контракте) принимает решение: покупать акции по цене K у первой стороны или нет. Решение принимается в зависимости от соотношения цены 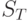и . Если 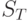< , покупать акции не выгодно, первая сторона получила прибыль C, а вторая – убыток C. В случае, если 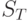> , вторая сторона покупает у первой акции по цене K, в ряде случаев получая прибыль (в зависимости от соотношения между C и ).

Основная проблема заключается в расчете справедливой цены такого опционного контракта – цены, при которой наблюдается баланс выигрыша/проигрыша каждой из сторон. Логично определить такую цену как средний выигрыш стороны :

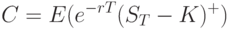( 4)

В формуле (4) равно либо разности между ценой акции в момент и ценой исполнения (если цена акции больше), либо нулю, – математическое ожидание (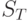 подвержена действию случайных факторов, смотри формулу (3)). Умножение на экспоненту соответствует т.н. дисконтированию – переводит 1 у.е. в момент времени 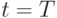к моменту времени , что соответствует инфляции с процентной ставкой r.

Метод вычисления справедливой цены опциона

Для вычисления справедливой цены опциона по формуле (4) известно аналитическое решение, которое справедливо при сделанных нами ранее предположениях.

Аналитическое решение описывается формулой Блэка–Шоулса для вычисления цены опциона в момент времени t = 0:

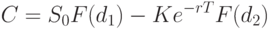( 5)

( 5)

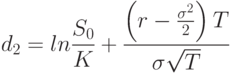( 5)

Именно эту формулу мы и будем использовать в дальнейших расчетах. Что же здесь считать? – спросите вы. Действительно, на первый взгляд все выглядит элементарным. На деле не все так просто, что мы и увидим далее.

Оценивание набора опционов

Конечно, для вычисления цены одного опциона не нужна высокопроизводительная вычислительная техника. На практике организации, работающие на финансовых рынках, вычисляют цены гигантского количества разных опционов, которые можно выпустить в конкретных рыночных условиях. Учитывая, что время финансовых расчетов существенно влияет на скорость принятия решений, каждая секунда на счету. Поэтому сокращение времени оценивания набора опционов является достаточно важной задачей.

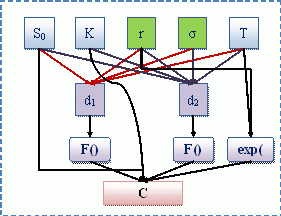
Построим схему информационных зависимостей для одного опциона ( рис. 9.1).

Рис. 9.1. Схема информационных зависимостей

При построении набора опционов в общем случае можно разрешить варьировать все 5 параметров (начальная цена акции, страйк, процентная ставка, волатильность, срок исполнения). Тем не менее, мы учтем тот факт, что параметры рынка (процентная ставка и волатильность) в конкретный момент времени одинаковы для всех опционов. Поэтому в дальнейшем в расчетах мы будем считать, что разные опционы отличаются начальной ценой акции, страйком и сроком исполнения.