Корректировка параметров, дистрибутивные преобразования, однослойные и совершенные логические нейронные сети

10.6. Корректное задание исходных данных – условие правильности выводов нейросети

Ранее не раз говорилось о "грамотном" задании исходных данных для адекватной реакции нейросети. Опыт пользователя должен развиваться на основе понимания логической и вероятностной взаимосвязей событий, являющихся предметом ее исследований. Необоснованное, случайное задание достоверности высказываний может привести лишь к утверждению известной шутки "каков вопрос – таков ответ".

Мы можем предварительно, на основе интуиции, лишь догадываться, что, например, достоверность высказывания "в билете указана дата (число) этого дня" зависит от достоверности высказывания "пассажир предъявил билет".

В "Математическая логика событий" для представления структуры взаимосвязанных событий рассматривались деревья логических возможностей (ДЛВ).

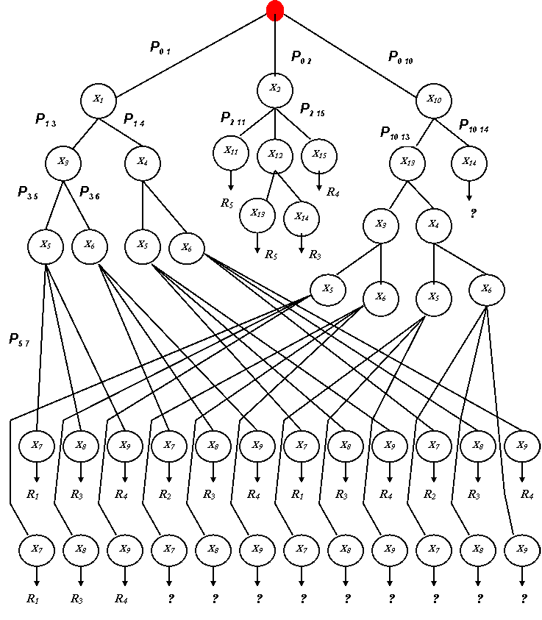
Составим дерево логических возможностей, связывающее вероятности событий, которые лежат в основе примера СПР (рис. 10.5), анализируемой в настоящей лекции.

При составлении ДЛВ учитывается, что каждое ветвление на основе некоторого события определяет исчерпывающее множество последующих событий при условии наступления данного. Следовательно, на ребрах (не на всех, чтобы не перегружать рисунок) указаны условные вероятности. Тогда полная вероятность некоторого события отыскивается как сумма произведений вероятностей, которые найдены по всем путям ДЛВ, приводящим к этому событию.

На основе анализа ДЛВ можно получать рекомендуемые диапазоны задания достоверности некоторых высказываний. Например, вероятность Р(Х₇) события Х₇ (в билете указан текущий год) находится следующим образом:

Для грубой оценки можно считать все элементы даты (число, месяц, год) независимыми и одинаково подверженными искажению. Тогда Р_{1 3} = Р_{3 5} = Р_{4 5} = Р_{5 7} = Р_{6 7} = Р, Р_{1 4} = Р_{3 6} = Р_{4 6} = 1 – Р, а Р(Х₇) = Р_{0 1}Р.

Если установлено, что в любом билете из-за неразборчивой печати каждый элемент даты обладает достоверностью Р = 0,9, и если, как в столбце 10 табл. 10.2, Х₁ = 0,5, то с достаточной точностью можно задать Х₃ = Х₅ = Х₇ = 0,45, Х₄ = Х₆ = 0,55, Х₈ = Х₉ = 0,5(1 – 0,45). Ветвь ДЛВ, обусловленная событием Х₂, не может быть исследована в вероятностном аспекте, т.к., например, предъявление или непредъявление пенсионного удостоверения – свершаемые события, обладающие единичной достоверностью.

увеличить изображение
Рис. 10.5. Дерево логических возможностей

Кроме того, возникает вопрос: почему при предъявлении неэталонных ситуаций величина максимального возбуждения нейронов выходного слоя часто превышает единицу? Ведь проводилась коррекция весов связей этих нейронов. Следует отметить, что на вход нейросети могут подаваться ситуации в самом непредсказуемом совмещении, отличном от идеального задания эталонов. Особенность и цель построения нейросети, как средства ассоциативного мышления, – возможность разобраться в наибольшей похожести. Коррекция весов связей по эталонам гарантирует лишь приблизительный интервал изменения величин возбуждения нейронов выходного слоя.

Таким образом, ДЛВ является вспомогательным средством, рекомендуемым пользователю на этапе обретения опыта, позволяющим учитывать явную зависимость событий и не допускающим абсурдных предпосылок при формировании вопросов нейросети.

Однако составление ДЛВ позволяет не только установить зависимость между достоверностью отдельных высказываний (событий), но и выявить те комбинации событий, т.е. ситуации, которые оказались неучтенными при проектировании СПР.

Пример 1. Что делать, если пассажир предъявил проездные документы, но не предъявил удостоверение работника МПС? Сформулируем вопрос нейросети, задав эталон этой ситуации, т.е. положим Х₁₀ = Х₁₄ = 1 и исследуем реакцию дистрибутивной нейросети на рис. 10.2 и однослойной нейросети на рис. 10.3. В обоих случаях получаем R₁ = 0,5, R₂ = 0,33, R₃ = R₄ = 0,5, R₅ = 0. Конечно, по данному эталону можно принять одно из рекомендуемых решений R₁, R₃, R₄, тем более что по ситуации, не известной сети, мог максимально возбудиться единственный нейрон выходного слоя, как рассмотрено ниже.

Пример 2. Обнаруживаем, что при логическом описании СПР не учтены все комбинации дат выдачи проездных документов. Сформулируем вопрос нейросети, задав непредусмотренную эталонную ситуацию Х₁₀ = Х₄ = Х₆ = 1. Обе нейросети отвечают максимальным возбуждением нейрона R₂. Рассчитывая на приблизительность, лежащую в основе ассоциативного мышления, можно вполне удовлетвориться полученным решением.

Однако с учетом предыдущего примера необходимо отметить, что нейросеть "фантазирует" и полагаться на адекватность ее выводов по непредусмотренным ситуациям не следует.

Несомненно, пробегающее по сети возбуждение при предъявлении непредусмотренной ситуации приводит к тому, что некоторый (некоторые) нейрон выходного слоя возбуждается более других, отвечая на вопрос: "на что более всего похожа данная ситуация?" Это так характерно для нашей жизни! Однако аналитический ум не удовлетворяется подобным ответом. Критический подход использует высокое значение порога достоверности на выходном слое.

Повысим значение порогов передаточной функции, реализуемой нейронами выходного слоя, положив их, например, равными 0,7. Тогда обе нейросети не будут реагировать на ситуацию в примере 1. Дистрибутивная нейросеть на рис. 10.2 не реагирует также на предложенную в примере 2 эталонную ситуацию, т.к. величина возбуждения нейрона R₂ составляла 0,66. Однако величина возбуждения этого нейрона в однослойной нейросети на рис. 10.3 составляла единицу, что требует дальнейшего повышения порога. Оно же может привести к ликвидации правильной реакции на предусмотренные ситуации. Ведь в столбце 9 табл. 10.2 максимальное возбуждение нейрона выходного слоя, обусловливающее адекватный вывод, составляет всего 0,95.

Если все же предъявленная ситуация "не одолела" предельно повышенный порог на выходном слое, ее следует считать не знакомой нейросети, не похожей ни на что, чему ее учили. Сеть требует вмешательства учителя, обучения новой ситуации.

В случае же возникновения "фантазий", не подвергающихся критическому анализу, можно предусмотреть самообучение нейросети, т.е. трассировку, закрепляющую новую причинно-следственную связь. Это справедливо в том случае, если "работа" нейросети, т.е. принимаемые ею решения, контролируются с помощью критериальной функции, оценивающей функционирование СПР. А именно: если решение, принятое в результате "фантазии", привело к удовлетворительному исходу, оно утверждается, и нейросеть получает разрешение на трассировку нового эталона.