Структурное обоснование логической нейронной сети

"...она остановилась подле вплоть мимо ее проходящего поезда. Она смотрела на низ вагонов, на винты и цепи и на высокие чугунные колеса медленно катившегося первого вагона и глазомером старалась определить середину между передними и задними колесами и ту минуту, когда середина эта будет против нее.

Л.Н. Толстой. Анна Каренина

9.1. "Железнодорожная рулетка"

Как показывает опыт пропагандирования нейросетевых технологий, молодежь слабо воспринимает материал, заставляя лектора каждый раз начинать с пояснения "на пальцах", что собой представляет нейросеть на абстрактном уровне и как она работает. Опасаясь, что наши пространные рассуждения выше отвратили нетерпеливого читателя, но надеясь, что он все же хочет выявить рациональное зерно, мы решили по случаю еще раз на примитивном уровне продемонстрировать подход, поймав читателя в ловушку и заставив его понять самый простой изначальный принцип.

Одновременно необходимо выявить ряд проблем, указывающих на то, что в предыдущих лекциях в области построения систем принятия решений сделано не все.

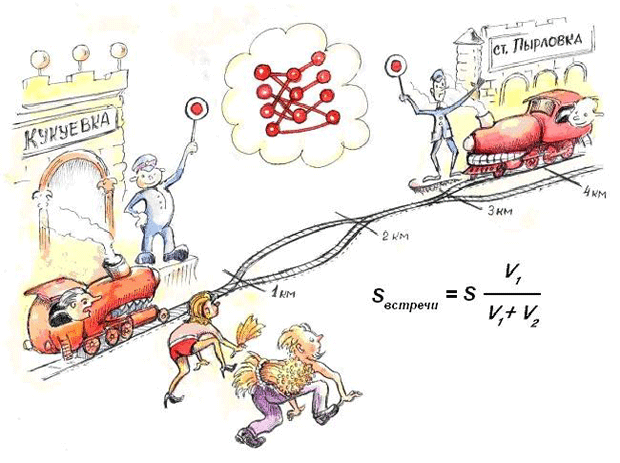
Построение обученной нейросети. Рассмотрим увлекательную детскую игру - "железнодорожную рулетку", - основанную на так хорошо знакомой вам задаче о встрече. Помните: "Из пунктов А и В навстречу друг другу " и т.д.?

Рис. 9.1. Железнодорожная рулетка

Начальник станции Кукуевка (старший) и начальник станции Пырловка одновременно выпускают навстречу друг другу два паровоза (рис. 9.1) со скоростью либо 60, либо 80 км/ч. Длина перегона составляет 4 км. Небольшой нюанс заключается в том, что пути перегона то сходятся в один, на протяжении одного километра, то расходятся. И тогда, в зависимости от точки встречи, со станции Кукуевка надо выслать на соответствующий километр либо линейного - даму с приветственным платочком, либо линейного с подстилочной соломкой.

Решение о такой посылке усложняется помехами в линии передачи данных, в связи с чем скорости паровозов сообщаются с достоверностью, меньшей единицы. Кроме того, необходимо каждый эксперимент связать с ожидаемыми денежными затратами на единовременную добавку к пенсии линейных.

В отличие от вас, начальник станции Кукуевка неважно учился в пятом классе, и решать оперативно подобную задачу, да еще при дополнительных условиях, не в состоянии. Он просит о помощи вас, предоставив в ваше распоряжение плохонький компьютер, отказанный в порядке шефской помощи Кукуевской начальной школой. Он объясняет вам, что не хочет считать вообще, а хочет добиться определенности по принципу "если , то ", а в случае недостоверных данных - "на что это более всего похоже и что делать?".

Тогда вы понимаете, что без элементов искусственного интеллекта не обойтись. Стимулируя свою изобретательность кружкой пива "Красный Восток", вы ищете что-то похожее на табличный метод, но с автоматической интерполяцией, что-то связанное с ассоциативным мышлением И вы решаетесь

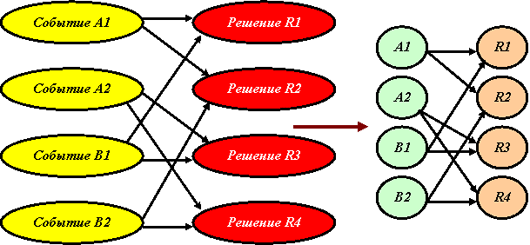
Произведем предварительные расчеты, чтобы представить себе все варианты будущего поведения нашей системы принятия решений - для ее обучения. Представим (рис. 9.2) графически структуру логического функционирования создаваемой системы принятия решений.

1. Кукуевский паровоз имеет скорость 60 км/ч (Событие А1 ). Пырловский паровоз имеет скорость 60 км/ч (Событие В1 ). Одновременное выполнение этих событий обозначим А1&В1. Тогда точка встречи находится как раз посредине перегона, что, скорее всего, требует помощи линейного с соломкой. Но возможно и везение за счет неточного определения скоростей. Тогда на всякий случай потребуется дама с платочком. Принимаемое решение, заключающееся в отправлении обоих линейных на границу второго и третьего километров, назовем решением R1. С ним связаны расходы на единовременное пособие М1.

   

   
   Рис. 9.2. Система принятия решений
2. Кукуевский паровоз имеет скорость 60 км/ч (Событие А1 ), но пырловский паровоз имеет скорость 80 км/ч (Событие В2 ). (Выполняется условие А1&В2.) Тогда их точка встречи находится на втором километре пути, и, следовательно, требует решения R2: "Отправить даму с платочком на второй километр!" В активе указанной дамы появляется сумма М2 условных единиц.
3. Кукуевский паровоз имеет скорость 80 км/ч (Событие А2 ), пырловский паровоз имеет скорость 60 км/ч (Событие В1 ). (Выполняется условие А2&В1.) Тогда их точка встречи находится на третьем километре пути, что требует сочувственного вмешательства линейного с соломкой (решение R3 ), с оплатой труда в М3 условных единиц.
4. Кукуевский и пырловский паровозы имеют скорость 80 км/ч (Событие А2&В2 ), что ввиду высокой скорости перемещения линейных требует решения R4 с затратами М4.

А теперь оживим эту структуру, заставим ее действовать, как, по-видимому, на логическом уровне действуют структуры нашего мозга.

Представим себе, что на месте каждого овала (потом - кружочка, на рис. 9.2 справа) действует нейроподобный элемент (просто нейрон). Нейроны входного слоя - рецепторы - приходят в возбужденное состояние (подобно сетчатке глаза) в соответствии с той ситуацией, которую мы задаем на входе системы. Например, мы хотим испытать ситуацию А1&В2. Тогда мы полагаем величины возбуждения нейронов А1 и В2 равными единице и записываем V_A1 = V_B2 = 1. При этом мы не забываем позаботиться о том, чтобы величины возбуждений нейронов А2 и В1 остались равными нулю.

Подчеркнем тот факт, что возбуждение нейронов-рецепторов осуществляется в результате ввода информации.

Для других нейронов, "принимающих" возбуждение в соответствии со стрелками, введем передаточную функцию, в результате выполнения которой формируется величина V возбуждения каждого нейрона. Для нашего случая, недолго думая (ибо существует большой произвол в выборе вида передаточной функции, на любой вкус), определим вид такой функции:

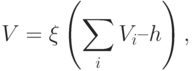
где i - индекс нейрона, "передающего" свое возбуждение данному нейрону, h - порог.

(Напомним: функция 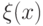заменяет отрицательную величину нулем, т.е.

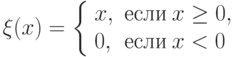
В нашем случае стрелки со всей определенностью указывают направление передачи возбуждений.

Положим h = 1 и рассчитаем величины возбуждения нейронов выходного слоя R1-R4 для ситуации А1&В2:

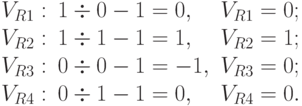
Таким образом, "высветилось" то решение, которое необходимо принять, и старт линейным должен быть дан. Проверим, что так же работает наша сеть по всем эталонам, по которым мы ее обучили, проложив "проводочки" от каждой исходной посылки к следствию.