Структурное обоснование логической нейронной сети

Отметим, что в "грамотно" построенной системе такие оценки могут быть вероятностными, являющимися оценками достоверности. Однако принципиально допустима и недостаточная грамотность пользователя. Например, он может быть не осведомлен о понятии исчерпывающего множества событий. Главное, чтобы оценки были относительными, отображающими принцип "больше - меньше" (аналогично экспертным системам), т.к. этого достаточно для моделирования ассоциативного мышления.

Однако конъюнкторы и дизъюнкторы определены лишь для булевых переменных. Следовательно, они должны быть заменены некоторым универсальным элементом, реализующим суррогат этих операций - передаточной функцией, способной на логическом уровне осуществлять схожую реакцию на сигналы на ее входе для получения оценочного сигнала на выходе. Это и привело к моделированию нейрона - основного логического элемента мозга, к воспроизведению искусственного интеллекта, одним из основных принципов которого является ассоциативное мышление.

На основе логической схемы (рис. 9.15) построим нейронную сеть той же структуры, обученную для решения нашей задачи. Вершины Х₁-Х₁₅ соответствуют нейронам-рецепторам входного слоя. От булевых значений их возбуждения перейдем к действительным - к оценкам достоверности соответствующих высказываний ("грамотный" вариант). Эти значения задаются пользователем скорее по наитию, "на глазок", на основе опыта.

Каждая конъюнкция высказываний в записи логических функций (9.1), т.е. совокупность событий, определяет ситуацию. Ситуация является эталоном (эталонной ситуацией), если все составляющие ее события обладают достоверностью, равной единице. В логической схеме каждой конъюнкции соответствует вершина из множества {1, ..., 11}. В нейронной сети эти вершины обозначают нейроны промежуточного или скрытого слоя. Нейроны R₁-R₅ образуют выходной слой; их возбуждение указывает на принимаемое решение.

Как говорилось выше, нейроны рецепторного слоя возбуждаются пользователем, задающим предполагаемую вероятность (или другую оценку) соответствующего события. Остальные нейроны реализуют передаточную функцию таким образом, чтобы возбуждение нейронов-рецепторов распространялось по сети в соответствии со связями. А именно, если, например, на входе сформирован высокий уровень возбуждения нейронов Х₁, Х₄, Х₇ по сравнению с возбуждением других нейронов-рецепторов, то большая величина возбуждения нейрона 2 должна обеспечить самое высокое возбуждение нейрона R₂ среди всех нейронов R₁-R₅ выходного слоя.

Отметим, что таким образом мы пытаемся построить уже обученную нейросеть, где по всем эталонным ситуациям максимального возбуждения должны достигать те нейроны выходного слоя, которые ответственны за решения, соответствующие этим ситуациям. Таким образом, реализуется таблица, о которой говорилось выше. Если же с помощью достоверности событий задавать на входе ситуации, явно не существующие, то нельзя гарантировать правильный ответ. Например, если достоверность всех событий Х₁ - Х₇ положить равной единице, то столь же бессмысленно будет распределение возбуждения нейронов выходного слоя. Или, если предположить, что мятая бумажка является предъявленным билетом с достоверностью 0,1 (событие Х₁ ), то полагать высоким значение достоверности события Х₈ не следует, т.к. эта достоверность является условной вероятностью, и т.д.

То есть логика мышления пользователя и знание элементов теории вероятности должны возобладать.

9.3. Выбор передаточной функции

Выбор передаточной функции остается творческой проблемой, во многом определяемой решаемой задачей. Важно лишь то, что полное копирование нейрона, созданного природой, излишне. В то же время передаточная функция - пороговая функция, активно использующая значение порога h.

В нейронных сетях учитывают веса связей - синапсические веса . Рассмотрение этих весов актуально, если структура сети первоначально задана и следует ее приспособить (обучить) для решения данной задачи. Пока мы рассматриваем построение уже обученной нейросети, поэтому вес сформированных связей принимаем равным единице. Однако далее будет показано, что корректировка весов необходима даже при построении обученных сетей. Эти веса могут быть скорректированы и в процессе эксплуатации для учета влияния событий на результат - принимаемое решение.

При выборе передаточной функции и порога h руководствуются следующими требованиями:

• эти функции в области преодоления порога должны монотонно возрастать по каждому сигналу на входе нейрона;
• не должно быть "угасания" сигнала возбуждения при его прохождении по сети;
• сигналы возбуждения на выходном слое должны быть четко различимы по величине для различных эталонных ситуаций ;
• должен быть примерно равным диапазон изменения величин возбуждения нейронов выходного слоя, закрепленных за разными решениями.

Практически, для логического решения задач, достаточно применять одну из следующих, например, используемых в [7], передаточных функций, определяющих величину V возбуждения нейрона в зависимости от величин V_i возбуждения связанных с ним нейронов, весов 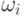этих связей, а также порога h:

1.

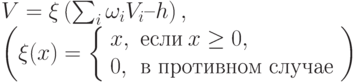
2.

3.

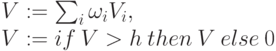
4.

5.

Поясним последнее требование к передаточной функции. Оно отражает, например, распознавание букв и знаков препинания. При этом целесообразно использовать передаточную функцию 3. Однако распознавание, например, запятой и буквы "А" приводит к резкому различию величин возбуждения соответствующих нейронов выходного слоя. При условии "шумов" запятая становится практически неразличимой, что приводит к необходимости преобразования величин возбуждения нейронов выходного слоя в единый диапазон изменения. Это либо достигается вводом в рассмотрение коэффициентов приведения, как в "Трассировка нейронной сети" , - для одинаковой коррекции всех весов связей каждого нейрона выходного слоя, либо приходится решать эту проблему отдельно для каждой связи такого нейрона, как будет показано далее. В рассматриваемом примере проблема уравнивания сигналов на выходном слое для различных эталонов также актуальна.

Таким образом, выбор и модификация передаточной функции производятся экспериментально, хотя легко установить общие черты функций, рекомендуемых здесь.

9.4. Анализ примера

Проверим, достаточны ли наши действия по построению нейросети. Показывает ли она на правильные решения по тем эталонным ситуациям, по которым создавалась логическая схема? Однозначен ли ее ответ при предъявлении различных эталонных ситуаций? Одинаковы ли величины возбуждения нейронов выходного слоя при предъявлении различных эталонов, что служит помехоустойчивости нейросети и возможности ее вложения в другие нейросети при формировании "длинных" логических цепочек рассуждений? Необходима ли коррекция параметров сети (порогов и весов связей) для ее правильной работы?

Отметим, что опыт исследований склоняет в пользу преимущественного применения передаточной функции 3. Она обладает таким важным свойством (если позволяет порог), как ассоциативность, позволяющая "собирать" сигнал независимо от пути прохождения возбуждения.

Выберем эту передаточную функцию, предположив, что веса всех связей равны единице, общий для всех нейронов порог h = 0,3.

Рассчитаем для различных эталонных ситуаций значения возбуждения нейронов выходного слоя и, следовательно, определим принимаемые решения. Расчеты сведены в табл. 9.1.

Анализируя таблицу, видим, что даже при предъявлении эталонов сеть работает неправильно. По некоторым эталонам (столбцы 1, 2 и 8) она дает неоднозначный ответ.

Тем самым сеть демонстрирует "побочный эффект". Из-за наличия общих событий, составляющих разные ситуации, эти события определяют одинаковый исход даже в том случае, если другие события обеспечивают различие ситуаций. Так, конъюнкция , определившая вместе с событиями Х₃ и Х₅ правильное решение R₁, дважды (нейроны 2 и 3 ) при использовании передаточной функции 3 участвуют в формировании возбуждения нейрона R₂ (столбец 1). Аналогичный вывод следует из анализа столбца 8. Необходимо подавить "побочный эффект", снизив величину возбуждения нейронов, не участвующих в возбуждении "нужного" нейрона выходного слоя. (Столбец 2 пока обсуждать не будем.)

Далее, анализ таблицы показывает, что даже при правильном ответе величины возбуждения нейронов выходного слоя, закрепленные за разными решениями, различны. Более того, эти величины могут различаться даже при предъявлении эталонов, требующих одного и того же решения (столбцы 1 и 2, 3 и 4, 8 и 9).

Таким образом, требуется корректировка параметров нейросети.