|
Раньше это можно было зделать просто нажав на тест и посмотреть результаты а сейчас никак |
Корректировка параметров, дистрибутивные преобразования, однослойные и совершенные логические нейронные сети
10.3. Дистрибутивная форма логического описания системы принятия решений
Приведенные выше построения предполагали представление логических выражений, описывающих СПР, в ДНФ. Однако известно, что каждое логическое выражение на основе алгебры высказываний может быть представлено и в виде конъюнктивной нормальной формы (КНФ). Такая форма также приводит к достаточности не более чем двухслойной нейросети. Мы не будем приводить такое представление для анализируемого примера, усложнившее описание СПР, но не приведшее к новым интересным выводам, однако сделаем общее замечание о важности минимизации количества слоев нейронной сети.
Развитие систем принятия решений, таких как медицинская или техническая диагностика, прогнозирование рынка ценных бумаг, управление перевозками железнодорожным транспортом и др., приводит к весьма большому числу исследуемых факторов и, следовательно, к еще большему числу нейронов сети. Расчет для каждого нейрона даже несложной передаточной функции в общем цикле обработки всех нейронов (в соответствии с их частичной упорядоченностью на основе преемственности информации) может привести к значительным временным затратам, ставящим под сомнение оперативность управления.
Необходима "аппаратная поддержка", что породило большое число предложений [14] в области разработки нейрокомпьютеров (НК), реализующих нейросети. В основе НК лежит принцип распараллеливания вычислений, что фактически означает распределение нейронов (программных процедур, моделей нейроподобных элементов и т.д.) между исполнительными вычислительными устройствами – процессорами для их обработки. Эффективны НК, выполненные в виде приставки к персональному компьютеру или рабочей станции. Ориентация НК на обработку универсальной двухслойной нейросети на основе ДНФ жестко распределяет функции слоев и возможные связи его процессоров, используя элементы стандартизации и унификации.
В "Математическая логика событий" обсуждалась проблема минимизации длины логической цепочки и было показано, что с помощью "размножения" решений такая длина может быть даже доведена до единичной.
Кроме того, известно [6], что эффективность распараллеливания, основным компонентом которой является минимум времени выполнения комплекса частично упорядоченных работ, зависит от длины критического пути в информационном графе, каким отображается нейросеть. Эта длина должна быть минимальной, что и обеспечивается не более чем двумя слоями нейросети. Следовательно, такая сеть гарантирует возможность оптимального распараллеливания.
Подобное заключение известно и специалистам по схемотехнике, всегда стремящимся минимизировать максимальную длину логической цепочки в схеме разрабатываемого устройства, влияющей на длительность такта его работы.
Однако, требуя обязательного представления логических выражений, описывающих СПР, в дизъюнктивной
нормальной форме, мы предполагаем скобочную запись, с открытыми относительно операции конъюнкции некоторыми
потенциальными скобками. Это, например, приводит к тому, что в выражении (9.1), определяющем решение R2,
дважды присутствует конъюнкция 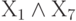 . В выражении, определяющем решение R3, дважды присутствует событие Х8 и т.д. При построении нейронной сети по логической схеме с использованием
передаточной функции, суммирующей сигналы, это привело к неоднократному учету некоторых сигналов в качестве
слагаемых. Так (см. табл. 9.1), расчет величины возбуждения нейрона R2 при предъявлении эталона 1 (по нему максимального возбуждения должен достичь
нейрон R1 ) требует сложения величин возбуждения нейронов 2 и 3,
каждая из которых формируется сложением сигналов Х1 и Х7. Это
и привело к побочному эффекту, с которым пришлось бороться соответствующим повышением порогов.
. В выражении, определяющем решение R3, дважды присутствует событие Х8 и т.д. При построении нейронной сети по логической схеме с использованием
передаточной функции, суммирующей сигналы, это привело к неоднократному учету некоторых сигналов в качестве
слагаемых. Так (см. табл. 9.1), расчет величины возбуждения нейрона R2 при предъявлении эталона 1 (по нему максимального возбуждения должен достичь
нейрон R1 ) требует сложения величин возбуждения нейронов 2 и 3,
каждая из которых формируется сложением сигналов Х1 и Х7. Это
и привело к побочному эффекту, с которым пришлось бороться соответствующим повышением порогов.
Тогда справедливо предположение о том, что, наоборот, вынесение за скобки способно не только упростить запись, обеспечив единственное вхождение переменных, но и тем самым исключить побочный эффект.
Для этого воспользуемся правилами эквивалентных преобразований. Определяющим в данном применении является симметричное свойство дистрибутивности конъюнкции относительно дизъюнкции и наоборот. (В алгебре применим лишь дистрибутивный, распределительный закон умножения относительно сложения.) Данное свойство (см. "Математическая логика событий" ) записывается как
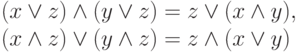
Предполагается возможность такого преобразования произвольной логической функции – композиции операций конъюнкции и дизъюнкции, при котором обеспечивается единственность вхождения каждой переменной в полученную запись. Основная операция, которая при этом используется – вынесение за скобку.
Однако, как следует из примера, рассмотренного в "Математическая логика событий" , такое преобразование не всегда приводит к успеху. Это свидетельствует о том, что в крайнем случае, для обеспечения единственности вхождения переменных, все же следует прибегать к способу "размножения" решений. Такое вынужденное "размножение" также отнесем к акту дистрибутивного преобразования.
Важность используемого в этом преобразовании свойства дистрибутивности приводит к целесообразности его учета в названии соответствующего логического описания СПР. Полученную таким образом нейросеть справедливо назвать нейросетью на основе дистрибутивного логического описания или просто дистрибутивной.
Упростим описание СПР, воспользовавшись операциями вынесения за скобки и выделения общих выражений:
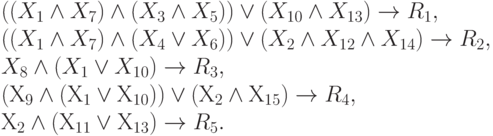 |
( 10.2) |
Наблюдается единственность вхождения каждого высказывания в описание логической функции (для сравнения см. (9.1)). При этом можно считать, что нам "повезло": "размножать" решения не потребовалось.
Форма представления (10.2) не только стала проще, она стала естественнее и понятнее. Однако наличие вложенных скобок вселяет сомнение в возможность использования не более чем двух слоев нейросети.
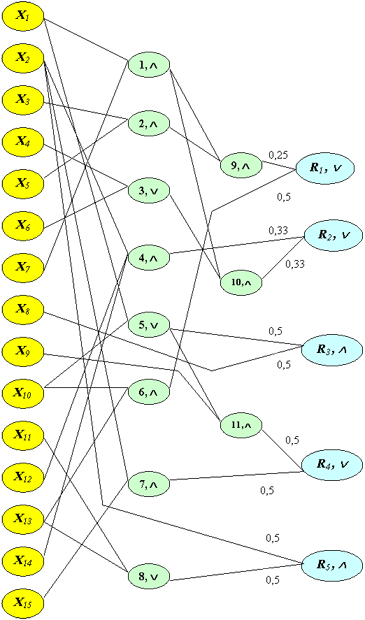
На рис. 10.2 (пока не следует обращать внимание на веса связей) отображена логическая схема реализации (10.2), она же – дистрибутивная нейросеть. Чтобы "не потерять" информацию, в кружках, обозначающих нейроны, указан тип логической операции прообраза – конъюнктора или дизъюнктора.
Выберем ту же передаточную функцию 3 и проверим, необходима ли здесь коррекция порогов и весов связей. Предварительно отметим, что описание (10.2) затрудняет перебор эталонных ситуаций. Для удобства их формирования все же воспользуемся аналогичной системой (9.1)-(10.1). Выберем малое значение порога h = 0,3, "не мешающее" суммированию сигналов, и, исключая очевидные вычисления, проанализируем отображение эталонных ситуаций.
Анализ показывает, что побочные эффекты отсутствуют. Это легко было предвидеть, т.к. выше их появление объяснялось неоднократным вхождением некоторых переменных–высказываний в одни и те же логические выражения при применении аддитивной передаточной функции.
При корректном задании исходной информации, т.е. при правильно сформулированном запросе на основе "физического смысла" СПР, имитируются функции конъюнкторов и дизъюнкторов – прообразов нейронов. То есть высокий уровень сигнала нейрона, принявшего роль конъюнктора, возникает в том случае, если все его входы предельно возбуждены. Нейроны, принявшие на себя роль дизъюнкторов, могут возбуждаться лишь при максимальном возбуждении одного из входов.
Однако величины возбуждения нейронов выходного слоя различны. Различаются и сигналы, приходящие на один нейрон от разных эталонных ситуаций.
Как и ранее, уточним веса связей нейронов выходного слоя (рис. 10.2). А именно, если нейрон принял роль дизъюнктора, то вес каждой связи уточняется отдельно по величине возбуждения, формируемой на основе соответствующего эталона. Новый вес равен единице, деленной на эту величину.
Если нейрон принял роль конъюнктора, то все веса его связей, до того равные единице, делятся на сумму сигналов, пришедших по всем связям при предъявлении соответствующего эталона, т.е. веса сохраняют одинаковые значения, а величина возбуждения этого нейрона становится равной единице.
Составим табл. 10.2 на основе расчета ситуаций, отображенных в табл. 10.1, и проанализируем ее. По эталонам (представлены не все, остальные легко рассчитать) сеть работает правильно.
По столбцу 8 видим, что сеть высказалась за решение R2. Этому решению следует больше доверять, т.к. высокое значение порога ранее существенно уменьшало величину распространяемого сигнала. Значение возбуждения R2, превышающее единицу, следует отнести за счет некорректности вопроса: предъявление пенсионного удостоверения или удостоверения работника МПС должно оцениваться исходя из условной вероятности, а именно, при условии, что билет не предъявлен. Таким образом, исходные оценки, подаваемые на рецепторный слой, предполагают структуризацию вопросов.
Столбец 9 демонстрирует довлеющую роль пенсионного удостоверения или удостоверения работника МПС, несмотря на подозрение на взятку, что исключает неоднозначность решения в табл. 10.1.
Столбец 10 свидетельствует о том, что полная неопределенность, следующая из предъявленных проездных документов, наказуема, хотя и малым штрафом.
| Решение | R1 | R2 | R2 | R2 | R3 | R4 | R5 | R2 | R5 | R2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Возбуждение нейронов выходного слоя | R5 | 0 | 0 | 0 | 0,25 | 0 | 0 | 1 | 0,55 | 0,95 | 0,25 |
| R4 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 1 | 0,5 | 0,55 | 0,8 | 0,65 | |
| R3 | 0,33 | 0,5 | 0,5 | 0 | 1 | 0,5 | 0 | 0,65 | 0,05 | 0,4 | |
| R2 | 0,67 | 1 | 1 | 1 | 0 | 0,33 | 0,33 | 1,2 | 0,33 | 1,43 | |
| R1 | 1 | 0,5 | 0,5 | 0 | 0,5 | 0,25 | 0,5 | 0,93 | 0,33 | 0,45 | |
| Возбуждение нейронов промежуточного слоя | 11 | 1 | 1 | 1 | 0 | 1 | 2 | 0 | 1 | 0,1 | 0,8 |
| 10 | 2 | 3 | 3 | 0 | 0 | 1 | 0 | 2,5 | 0,1 | 1,8 | |
| 9 | 4 | 2 | 2 | 0 | 0 | 1 | 0 | 3,1 | 0,1 | 1,8 | |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | |
| 7 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0,1 | 1,5 | 0,5 | |
| 6 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0,1 | 0,6 | 0 | |
| 5 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0,1 | 0,5 | |
| 4 | 0 | 0 | 0 | 3 | 0 | 0 | 1 | 1,1 | 0,9 | 2,5 | |
| 3 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0,7 | 0 | 1 | |
| 2 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 1,3 | 0 | 1 | |
| 1 | 2 | 2 | 2 | 0 | 0 | 1 | 0 | 1,8 | 0,1 | 0,8 | |
| Ситуация | X15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0,6 | 0 |
| X14 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | |
| X13 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0,6 | 0 | |
| X12 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
| X11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0,4 | 0 | |
| X10 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0,1 | 0 | 0 | |
| X9 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0,3 | |
| X8 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0,1 | 0 | 0,3 | |
| X7 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0,9 | 0 | 0,3 | |
| X6 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0,5 | 0 | 0,5 | |
| X5 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0,5 | 0 | 0,5 | |
| X4 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0,2 | 0 | 0,5 | |
| X3 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0,8 | 0 | 0,5 | |
| X2 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0,1 | 0,9 | 0,5 | |
| X1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0,9 | 0,1 | 0,5 | |
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
Таким образом, нейросеть отражает здравый смысл, склоняясь к вполне обоснованному, подобно карточному гаданию, решению.