|
Раньше это можно было зделать просто нажав на тест и посмотреть результаты а сейчас никак |
Основы нейросетевых технологий
2.1.2. Обучение нейросети
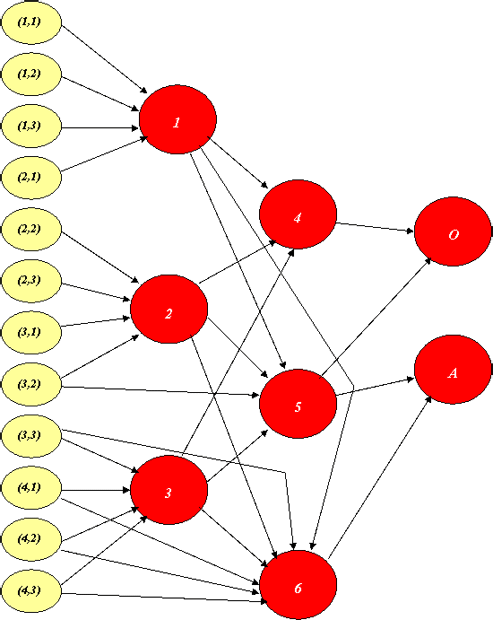
Теперь предположим, что структура сети (рис. 2.5), а также передаточная функция (та же), заданы, и нам предстоит обучить сеть распознаванию букв О и А.
Пусть экран разбит на столько же клеток, и мы убеждаемся лишь в том, что предложенная нейросеть содержит не менее 12 нейронов входного слоя, а также не менее двух нейронов выходного слоя.
Теперь возникла необходимость отразить истинный характер преобразования нейроном входной информации,
т.е. величин возбуждения нейронов, связанных с ним. Дело в том, что все входы нейронов обладают регулируемыми
(!) весами (синапсическими весами, весами связей), позволяющими направлять прохождение возбуждения в сети. С помощью
этого регулирования можно связывать конфигурации и возбуждения нейронов входного слоя
(посылка) с максимальным возбуждением определенных нейронов выходного слоя (следствие),
формируя связи "если  , то
, то  ".
".
В связи с этим передаточная функция нейрона, в частности заданная нам или выбранная нами сознательно, имеет общий вид

Здесь 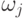 - синапсический вес входа или вес связи, по которой передается
возбуждение от нейрона j нейрону i.
- синапсический вес входа или вес связи, по которой передается
возбуждение от нейрона j нейрону i.
Тогда задачей обучения является выбор высоких весов некоторых связей и малых весов других связей так, чтобы в соответствии с функциональным назначением сети сложились отношения "посылка - следствие", подобные тем, которые мы создали выше при построении уже обученной сети. Они переводят возбуждение рецепторов, образующееся при "показе" эталонов и образов, в максимальное возбуждение тех нейронов выходного слоя, которые говорят, "что это такое".
Для простоты положим максимальный вес связи единичным, а минимальный оставим нулевым. Это соответствует тому, что, интерпретируя связи в сети как "проводочки", мы какие-то из них оставим (считая их сопротивление нулевым), а другие, ненужные, "перекусим".
Изложенная идея обучения по четко заданным эталонам воплощена в алгоритме трассировки нейросети.
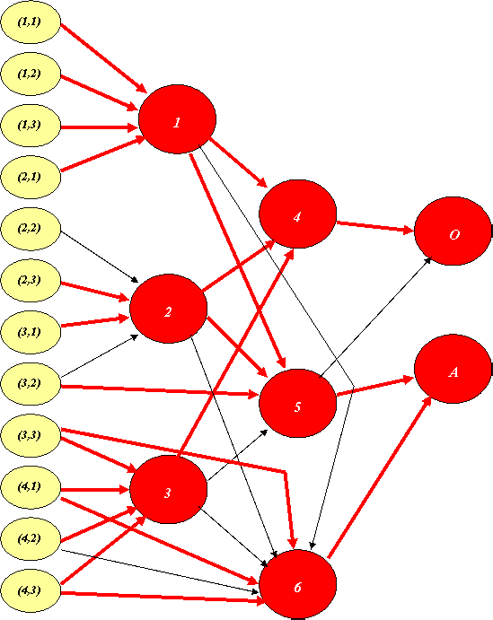
На рис. 2.6 приведен результат такой трассировки для нашего примера, где выделенные стрелки соответствуют связям с единичными весами, а другие - с нулевыми.
Просчитав несколько, в том числе "неопределенных", образов на входе, можно убедиться в ее правильной работе, хотя и демонстрирующей изначально выбранное слабое отличие О от А.
Получилась интересная игра. Мы задаем на входе случайные возбуждения и спрашиваем: на что это больше похоже из того, что "знает" нейросеть? Все, что надо сделать, это посчитать в едином цикле для каждого нейрона значение передаточной функции и проанализировать величины возбуждения нейронов выходного слоя.