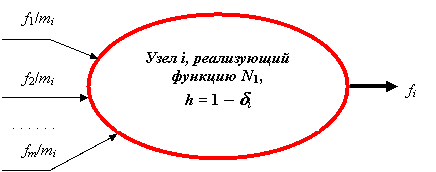Математическая логика событий

1.8. Системы принятия решений на основе достоверности высказываний о событиях

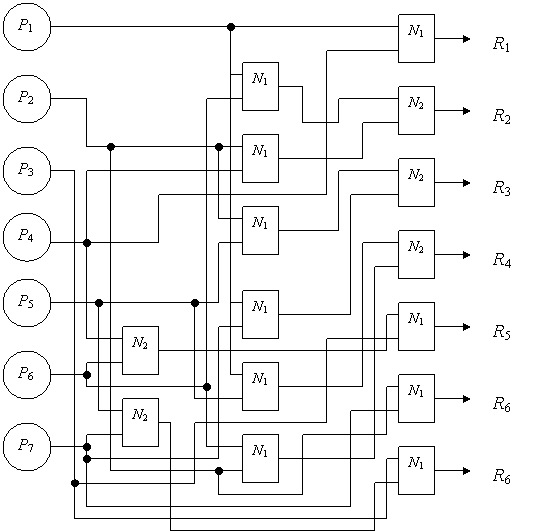
Изменения, внесенные в дерево логических возможностей и представленные на рис. 1.5, отобразим в электронной схеме системы принятия решений, представленной на рис. 1.4. Теперь исходными данными (рис. 1.6) для конъюнкторов и дизъюнкторов, принимающих эти данные, становятся не булевы, а действительные значения, для которых логические операции не определены.

Рис. 1.6. Система принятия решений на основе достоверности событий

Следуя далее по пути приблизительных оценок (ибо практически достоверность, как категория теории вероятностей, принадлежит области весьма приблизительных оценок), разработаем некоторый суррогат операций конъюнкции N₁ и дизъюнкции N₂ на основе передаточной функции порогового элемента, преобразующего сумму входных величин в выходные значения, которые приближенно "напоминают" результаты упомянутых логических операций. Этот путь - путь ухода от точного выбора решения в сторону выбора решения на основе степени похожести ситуаций на уже известные, - путь ассоциативного мышления.

Существует множество вариантов подбора пороговой передаточной функции, лежащей в основе такого элемента.

Введем сквозную нумерацию всех узлов схемы, реализующих дизъюнкцию и конъюнкцию. Пусть i - номер такого узла, j - номер входа этого узла при количестве m_i активных входов (в данном примере каждый узел имеет два входа), 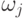- вес входа. Тогда простейшая передаточная функция f_i, реализуемая i -м узлом для замены логических операций конъюнкции и дизъюнкции, имеет вид

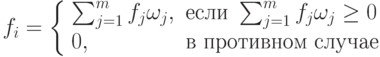( 1.18)

Здесь f_j - величина сигнала, поступающая на j -й вход.

Тогда элемент N₁, подобный конъюнктору, может быть реализован при 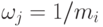, j =1, ..., m_i, с помощью существенно высокого порога (рис. 1.7), где значение 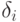обусловлено некоторой поправкой, достаточной, чтобы для преодоления порога сигналы возбуждения с большой степенью уверенности поступали обязательно по всем входам.

Рис. 1.7. Элемент N1

На этапе настройки и верификации СПР предполагается, что входные сигналы - булевы переменные, принимающие значения 0, 1. Тогда целесообразно выбрать значение . Очевидно, что для того, чтобы преодолеть порог, на всех входах должны быть "1"; недостаток хотя бы одной "1" приведет к тому, что сумма поступивших сигналов будет более чем на 1/m_i меньше указанной суммы весов.

При переходе к действительным переменным, когда вместо событий рассматриваются, например, лишь предполагаемые вероятности их наступления, экспериментальный выбор значения 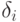может обусловить ту границу, когда считаться с возможностью данной комбинации событий нецелесообразно.

Элемент N₂, подобный дизъюнктору, реализуется, наоборот, при низком значении порога и при . Порог выбирается так, чтобы уже при возбуждении на одном входе возникал сигнал возбуждения на выходе. При этом сигнал на выходе не превышает "1" (рис. 1.8), а значение 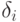выбирается экспериментально достаточно небольшим.

Рис. 1.8. Элемент N2

Задав на входе СПР значения достоверности переменных-высказываний и рассчитав значения на выходах пороговых элементов, на выходах схемы получим некоторые значения. Максимальное из этих значений "голосует" в пользу соответствующего решения.

Предложения, касающиеся создания пороговых элементов N₁ и N₂, носят лишь рекомендательный характер. Здесь неограниченный простор для творчества.

Напомним, что корректность задания исходной информации (соблюдение условия нормировки на исчерпывающих множествах событий, оценки достоверности с помощью вероятностного дерева логических возможностей ) гарантируют практически приемлемый результат. Если же на входах задавать что угодно, то СПР преобразует это в какую угодно рекомендацию по принципу "каков вопрос - таков и ответ".

На рассмотренном жизненном примере проанализируем принимаемые бабушкой решения на основе двух вариантов СПР: с помощью электронной схемы (рис. 1.4), использующей определенность знания о ситуации, и с помощью схемы, основанной на неопределенности, на предполагаемой достоверности этих знаний (рис. 1.6). Положим (на основе интуиции) для всех i.

Данные сведены в табл. 1.2.

Более точный выбор значения 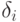производится на основе верификации СПР по известным вариантам нахождения решения. В данном случае представляется, что этот выбор произведен успешно.