|
Раньше это можно было зделать просто нажав на тест и посмотреть результаты а сейчас никак |
Московский государственный университет путей сообщения
Опубликован: 01.06.2007 | Доступ: свободный | Студентов: 1914 / 103 | Оценка: 4.38 / 3.75 | Длительность: 22:59:00
ISBN: 978-5-9556-0094-9
Специальности: Программист
Теги:
Лекция 1:
Математическая логика событий
1.5. Система принятия решений
Для некоторой логической функции f от переменных из факторного пространства событий воспользуемся операцией следования (импликации) и сформируем логическое выражение вида
 |
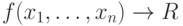( 1.15) |
Здесь f следует рассматривать как выражение, определяющее условие, сложившуюся ситуацию,
посылку, а R - высказывание, которое рассматривается
как следствие: правило поведения, значение векторной функции, указание к действию и т.д. Таким образом, возможно
формирование связей вида "посылка - следствие", "если 
, то ". При этом функция f задается на множестве ситуаций и указывает на то, что, если на некоторой ситуации она принимает значение
1 (ИСТИНА), то такое же значение принимает высказывание R, являясь руководством
к действию, к принятию определенного решения.
Подобно (1.17), можно описать множество логических выражений, определяющих стройную систему управления или принятия решений в соответствии со складывающейся ситуацией в факторном пространстве событий:
 |
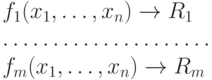( 1.16) |
Определение 6. Система логических выражений вида (1.16), заданная на факторном пространстве (подпространстве) событий, обладающая полнотой и непротиворечивостью, называется системой принятия решений .
Поясним важность свойств, указанных в определении.
То, что система функций f1, ..., fm является полной, означает, что любая точка факторного пространства событий входит в область задания хотя бы одной из этих функций. Непротиворечивость означает, что по каждой ситуации одна и только одна из этих функций принимает значение 1, приводящее к истинности соответствующего высказывания - решения. Однако отметим, что в действительности на основе смыслового содержания задачи по каждой или некоторой ситуации может быть известно более одного правильного решения, приводящего к успешным действиям. В таком случае высказывания об этих решениях могут быть объединены операцией ИЛИ, что приводит к приведенному выше предположению о непротиворечивости.
Продолжим рассмотрение примера.
Пусть известная нам бабушка планирует занятия физкультурой и спортом во все времена года по времени
дня: после завтрака, после обеда и после ужина. Объединяя высказывания по принципу "если ,
то" и пользуясь обозначениями на рис. 1.1, она формирует систему принятия решений, которой, не полагаясь на память, намерена
строго следовать, добившись согласия администрации.
Система имеет вид
 |
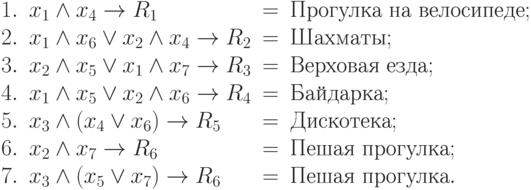( 1.17) |
Планируя пешую прогулку, бабушка первоначально получила следующее выражение:
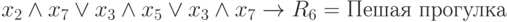
Однако выше не напрасно обращается внимание на целесообразность однократного вхождения переменных в подобное выражение (это будет изучено в "Структурное обоснование логической нейронной сети" и "Корректировка параметров, дистрибутивные преобразования, однослойные и совершенные логические нейронные сети" ). Выражение, полученное первоначально, с помощью дистрибутивных преобразований привести к такому виду не удается. Тогда бабушка решает разбить это выражение на два подобных, сформировав получение одного и того же решения на основе двух условий. Это и послужило появлению в (1.17) двух выражений, определяющих одно решение R6.
Легко убедиться, что все возможные ситуации факторного пространства событий охвачены, демонстрируя полную ясность действий бабушки.
Системы принятия решений могут образовывать сложные иерархические структуры. В этом случае необходимо, чтобы высказывания- решения R1, ..., Rm отображали события, образующие ИМС.
1.6. "Схемотехническое" представление системы принятия решений
Отобразим (c нарушением некоторых стандартов) схемотехнически бабушкину СПР, подобно электронной схеме (рис. 1.4) с помощью конъюнкторов и дизъюнкторов. На вход будем подавать значения истинности переменных-высказываний (ситуации) так, чтобы на одном из выходов формировалась единица - значение истинности соответствующего решения. Задавать значение ситуаций следует корректно, чтобы соблюдать требования вхождения переменных в исчерпывающие множества событий.
Реализовав эту схему на логических элементах, бабушка получит реальное средство подсказки: что она должна делать в данное время года и суток.
Например, бабушка хочет вспомнить, чем она должна заниматься летом после обеда. Она полагает x2 = x5 = 1 при нулевых значениях других переменных и запускает программу, моделирующую работу электронной схемы. На выходе R3 формируется сигнал, соответствующий высказыванию "Верховая езда".
Электронная схема, имитирующая систему принятия решений, требует корректного задания исходной информации, т.е. корректной формулировки вопроса в соответствии со смыслом задачи. Одновременно должна существовать уверенность в получении единственного решения, в том числе предполагающего задание альтернативных вариантов, если это предусмотрено при построении СПР. В таком случае окончательный выбор альтернативы может быть предусмотрен при развитии системы, при анализе новых вводимых факторов. При некорректной формулировке вопроса возникнут коллизии, неоднозначные или неправильные выводы. Таким образом, СПР может отвечать только на те вопросы, на которые она настроена.
