| Россия, Сургут |
Матрицы
В этой лекции мы собираемся представить введение в алгебру матриц -технику вычислений, применяемую при выполнении линейных трансформаций.
Начнем с определения скалярного произведения в 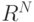 . Скалярное произведение двух векторов в
. Скалярное произведение двух векторов в 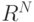 - это число, определяемое следующим образом:
- это число, определяемое следующим образом:
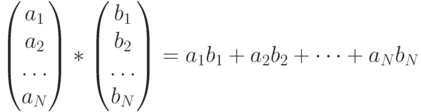
Скалярное произведение билинейно:
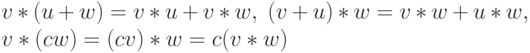
и симметрично: v*w = w * v.
Еще одно важное свойство скалярного произведения состоит в том, что оно позволяет вычислить длину вектора. Будем обозначать длину вектора v как |v| . Тогда: 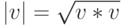 . Длина вектора называется также его нормой.
. Длина вектора называется также его нормой.
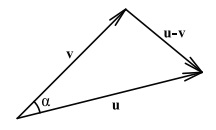
На плоскости соотношение для |v| прямое следствие теоремы Пифагора:
Для вектора 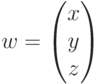 в трехмерном пространстве теорему Пифагора применяем дважды, вначале для проекция вектора на плоскость XY:
в трехмерном пространстве теорему Пифагора применяем дважды, вначале для проекция вектора на плоскость XY: 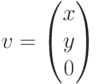 ,
,
получив 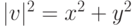 , затем к вектору v и перпендикулярному вектору
, затем к вектору v и перпендикулярному вектору 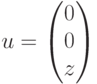 . В результате получаем:
. В результате получаем: 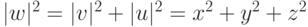
Для установления истинности формулы 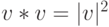 в
в 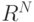 теорему Пифагора следует применить N - 1 раз.
теорему Пифагора следует применить N - 1 раз.
Теорема. Пусть u, v - два вектора в 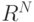 с углом
с углом  между ними. Тогда
между ними. Тогда 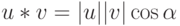 .
.
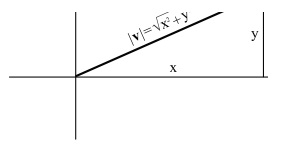
Доказательство. Рассмотрим треугольник, сформированный векторами u, v, u-v. По свойству скалярного произведения:
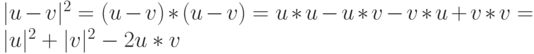
С другой стороны по теореме косинусов:
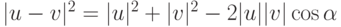
Из сравнения этих формул следует истинность утверждения теоремы.
Следствие. Два вектора в 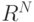 перпендикулярны друг другу если и только если их скалярное произведение равно нулю.
перпендикулярны друг другу если и только если их скалярное произведение равно нулю.
Определение. Матрица линейной трансформации Т векторного пространства 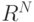 - это квадратная таблица N * N из N строк и N столбцов, содержащих числа, сформированная векторами
- это квадратная таблица N * N из N строк и N столбцов, содержащих числа, сформированная векторами 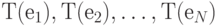 , представляющих столбцы матрицы.
, представляющих столбцы матрицы.
Пример. Пусть Т - поворот на 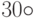 против часовой стрелки. Тогда:
против часовой стрелки. Тогда:
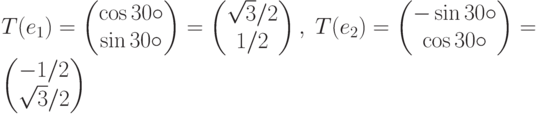
Матрица, задающая Т, имеет вид:
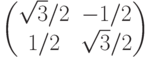
В общем случае матрица трансформации, задающая на плоскости поворот против часовой стрелки на угол  , имеет вид:
, имеет вид:
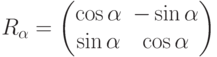
Как мы видели в предьцдущей главе, линейная трансформация определяется трансформациями базисных векторов. Следовательно, в матрице линейной трансформации содержится вся информация о трансформации.
Теперь мы определим операцию умножения матрицы на вектор из 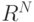 .
.
Определение. Произведение Аv квадратной матрицы А размера N * N на вектор v из 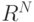 - это вектор в
- это вектор в 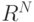 , k-ая компонента которого представляет скалярное произведение k-й строки матрицы А на вектор v.
, k-ая компонента которого представляет скалярное произведение k-й строки матрицы А на вектор v.
Теорема. Пусть Т-линейная трансформация в 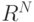 , определяемая матрицей А, тогда результат применения Т к вектору v эквивалентен произведению Аv.
, определяемая матрицей А, тогда результат применения Т к вектору v эквивалентен произведению Аv.
Мы не станем рассматривать формальное доказательство, а рассмотрим пример. Пусть Т - линейная трансформация в  , определяемая матрицей А:
, определяемая матрицей А:
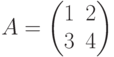
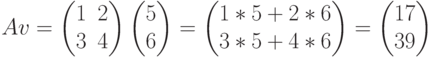
Результат применения трансформации Т к вектору v:
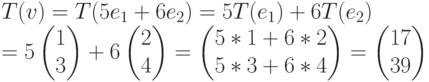
Нетрудно видеть, что эти вычисления остаются справедливыми в общем случае для любых матриц размера N * N и векторов v из 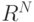 .
.
Упражнение. Пусть Т - отражение плоскости относительно прямой у = 2х. Найти матрицу, задающую трансформацию Т.
Решение. Для формирования матрицы необходимо найти  и
и  . Покажем на этом примере, как это можно сделать. Выберем два вектора, для которых трансформация Т известна. Для вектора
. Покажем на этом примере, как это можно сделать. Выберем два вектора, для которых трансформация Т известна. Для вектора 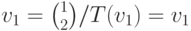 , поскольку точка (1,2) принадлежит прямой у = 2х. Для вектора
, поскольку точка (1,2) принадлежит прямой у = 2х. Для вектора 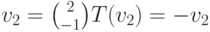 , поскольку скалярное произведение векторов
, поскольку скалярное произведение векторов 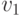 и
и 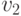 равно 0, следовательно, вектора
равно 0, следовательно, вектора 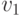 и
и 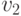 перпендикулярны.
перпендикулярны.

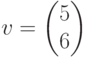 , тогда
, тогда