НОУ ИНТУИТ | Информационные основы вычислительной техники. Лекция 8: Умножение чисел с фиксированной запятой в прямом и дополнительном кодах

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 05.06.2018 | Уровень: для всех | Доступ: платный

|

Вам нравится? Нравится 11 студентам

| Поделиться |

Поддержать программу

Умножение со старших разрядов множителя чисел, заданных в прямом коде

Напомним, что при реальной записи числа в памяти ЭВМ какие-либо символы, отделяющие знак от цифровой части числа, отсутствуют. Так что в данном случае мы имеем дела с пятиразрядным числом, включающим знак и четыре цифровых разряда.

Так как в прямом коде знак произведения и его модуль формируются отдельно, то следует обсудить лишь вопросы, касающиеся количества разрядов, отводимых под хранение мантисс сомножителей и мантиссы произведения.

Мы уже отмечали, что произведение следует получать в 2n-разрядной сетке, где n – количество разрядов у операндов.

Умножение со старших разрядов множителя заключается в том, что за время умножения на один разряд множителя происходит два действия:

к сумме частичных произведений (СЧП) добавляется $\left |X\right |$ , сдвинутый вправо на количество разрядов, соответствующее анализируемому знаку множителя, либо добавляется ноль, если анализируемый знак множителя был равен нулю;
регистр сдвига, хранящий $\left |X\right |$ , сдвигается вправо на 1 разряд.

В силу того, что в операции должны участвовать операнды одинаковой разрядности, а разрядность результата, равна 2n, то и $\left |X\right |$ изначально должен храниться в регистре длиной 2n, в котором младшие n позиций заполнены нулями. Также изначальное значение СЧП тоже должно быть равно нулю и изначально все ее позиции должны быть заполнены нулями. Для СЧП может быть выбран обычный регистр хранения: исходя из формулы (8.2) его значение сдвигам не подвергается.

Регистр, хранящий $\left |Y\right |$ , в процессе выполнения умножения интересен не как единое целое, а как набор отдельных разрядов, хранящих значения y_i, использующихся при формировании очередного СЧП. Получение очередного значения y_i в следующем такте формирования СЧП может быть выполнено разнообразными схемотехничекими решениями, наиболее рациональным из которых представляется хранение $\left |Y\right |$ в n-разрядном регистре сдвига, его сдвиге в сторону старших разрядов после анализа очередного разряда и снятии старшего разряда этого регистра в каждом такте для анализа очередного разряда y_i.

Таким образом, мы получаем следующие схемотехнические требования к регистрам, которые хранят модули операндов и результата:

RG |X| – разрядность 2n, возможность сдвига вправо;
RG |Y| – разрядность n, возможность сдвига влево;
RG СЧП (RG |Z|) – разрядность 2n c возможностью первоначальной установки в ноль.

Пример 8.2.

Умножить два числа с фиксированной запятой, заданных в прямом коде, со старших разрядов множителя: X_пк = 1.0110, Y_пк = 0.1010.

Исходя из вышесказанного, выполнение данного примера будет складываться из следующих этапов.

Определяем знак произведения согласно формуле (8.1):
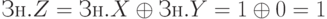
$Зн.Z = Зн.X \oplus Зн.Y = 1 \oplus 0 = 1$
Определяем модуль произведения согласно формуле (8.2):

Так как в формировании произведения участвует $\left |X\right |$ , сдвинутый на соответствующее число разрядов вправо, то для наглядности будем представлять его в виде отдельного столбца значений.
Получаем итоговый результат Z = 1.00111100_пк

На основе данного примера рассмотрим еще один момент, отражающий связь между используемым при выполнении арифметических действий алгоритмом и особенностями организации ЭВМ. При умножении со старших разрядов множителя чисел, заданных в прямом коде, к значению СЧП, полученному на очередном шаге, в зависимости от значения очередного разряда y_i добавляется либо $\left |X\right |$ , сдвинутый на соответствующее количество разрядов вправо, либо ноль. Добавления ноля, казалось бы, только замедляет выполнение операции (в половине случаев такое сложение бессмысленно). Однако, и тот, и другой вариант действий может быть использован. Первый вариант носит название варианта без пропуска такта суммирования, а второй, соответственно, с пропуском такта суммирования.

В качестве преимущества первого варианта мы отметили устранение операции суммирования с нулем, которое не приводит к изменению предыдущего значения СЧП. Но при этом у нас изменяется регулярность последовательности тактов выполнения операции умножения, а само значение y_i должно быть передано и проанализировано устройством управления компьютера, которое является сложной и нерегулярной схемой. В то же время прибавление нуля к СЧП (при y_i = 0) можно осуществить достаточно просто. Фрагмент такого действия показан на Рис. 8.6. Более подробно арифметико-логическое устройство, реализующее такой алгоритм умножения, показано в [ ].

Рис. 8.6. Управление передачей |X|•2 в степени -i на сумматор СЧП в алгоритме без пропуска такта суммирования

Умножения с младших разрядов множителя чисел, заданных в прямом коде

Данное умножение реализуется согласно формуле (8.3). Суть этой формулы проста: к СЧП, полученной на предыдущем шаге добавляется $\left |X\right |$ , умноженный на значение соответствующего разряда y_i, а затем полученное новое значение сдвигается вправо на 1 разряд. Нюанс этого алгоритма как раз и заключается в этом сдвиге, завершающем формирование очередного значения СЧП.

Так как для данного формата |X| > 1 и |Y| < 1, то их произведение тоже не превышает единицы, и в процессе вычислений никаких особых мер предосторожности применять не нужно. Но так как каждый шаг обработки очередного разряда множителя заканчивается умножением полученной перед этим суммы на 2^-1, то есть фактически ее уменьшением в два раза, то это означает, что в процессе умножения вплоть до самого последнего этапа при сложении возможно получение числа, превышающего единицу. Это возможное превышение как раз и компенсируется сдвигом.

Для корректного пошагового выполнения умножения по этому алгоритму рекомендуется применять модифицированный код. При этом сдвиг числа, заданного в модифицированном коде, на i разрядов вправо (умножение на 2^-i) проводится по схеме, представленной на Рис.8.7:

Рис. 8.7. Схема сдвига вправо для числа, представленного в модифицированном коде

Пример 8.3.

Выполнить умножение с младших разрядов множителя следующих чисел с фиксированной запятой, заданных в прямом коде:

X_пк = 1.1101

Y_пк = 1.1011

Решение.

$Зн.Z = Зн.X \oplus Зн.Y = 1 \oplus 1 = 0$
$Z _{пк} = Зн.Z. \left | Z \right | = 0.10001111_{пк}$

Умножение со старших разрядов множителя чисел, заданных в дополнительном коде

Выполнение операции умножения в случае, когда сомножители заданы в дополнительном коде, имеет другую структуру, нежели умножение в прямом коде. Главное отличие состоит в том, что в формировании произведения участвуют сомножители целиком, вместе со своими знаками. Произведение также формируется вместе со знаком.

При выполнении операции умножения со старших разрядов множителя формула (8.2) приобретает следующий вид:

$Z_{дк} = 0 + (y_1-y_0)\bullet X_{дк}\bullet2^0 + (y_2-y_1)\bullet X_{дк}\bullet 2^{-1} + ... + (y_{n+1}-y_n) \bullet X_{дк} \bullet 2^{-n}$

( 8.3)

Эта формула имеет следующие особенности:

y₀ – знаковый разряд множителя;
y_n+1 – фиктивный разряд расширения длины множителя, который для дополнительного кода всегда принимается равным нулю (при этом значение самого числа вне зависимости от его знака не меняется);
(y_i+1-y_i) может принимать значения нуля (при равенстве соседних разрядов множителя), (+1) или (-1). В двух последних случаях при получении СЧП необходимо к предыдущему значению СЧП добавлять сдвинутые на соответствующее количество разрядов вправо X_дк или (-X_дк) в первом и втором случае соответственно;
так как в дополнительном коде можно представить на одно отрицательное число больше, чем в прямом коде и на последнем шаге сдвиг вправо результата не выполняется, то процесс умножения можно проводить в обычном, а не модифицированном коде.

Рассмотрим это на следующем примере.

Пример 8.4.

Выполнить умножение со старших разрядов множителя следующих чисел с фиксированной запятой, заданных в дополнительном коде: X_дк = 1.0011; Y_дк = 1.1011

Решение.

Дальше >>

Информационные основы вычислительной техники

Информационные основы вычислительной техники