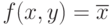| Россия, г. Москва |
Инспектор
Вы можете этот курс.
Опубликован: 05.06.2018 | Уровень: для всех | Доступ: платный
Лекция 1:
Основные понятия алгебры логики. Функции алгебры логики. Основные логические эквивалентности
Представление логической функции в виде таблицы истинности
Прежде всего, определимся с понятием "элементарная логическая функция". Чаще всего,это понятие в литературе никак не расшифровывается. В дальнейшем мы будем понимать под "элементарной логической функцией" ФАЛ от аргументов, каждый из которых, в свою очередь, не является логической функцией и которые имеют своё собственное обозначение.
Таблица истинности указывает значение логической функции при всех значениях наборов аргументов. Ниже мы рассмотрим элементарные логические функции от одной и двух переменных.
Все возможные элементарные логические функции от одной переменной представлены в Табл. 1.1:
| Функция | x | Наименование функции | Обозначение функции | |
|---|---|---|---|---|
| x=0 | x=1 | |||
| ƒ0 | 0 | 0 | Константа "ноль" | ƒ(x)=0 |
| ƒ1 | 0 | 1 | Тождественная функция | ƒ(x)=x |
| ƒ2 | 1 | 0 | Отрицание |  |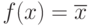
| ƒ3 | 1 | 1 | Константа "единица" | ƒ(x)=1 |
Здесь интерес представляет лишь одна функция – отрицание. Опишем ее основные свойства:
Последнее свойств можно описать как "отрицание отрицания есть утверждение".
Все возможные логические функции от двух переменных представлены в Табл. 1.2:
|
№ функции |
Значение функции на наборах логических переменных | Наименование функции | Обозначение функции | |||
|
x=0 y=0 |
x=1 y=0 |
x=0 y=1 |
x=1 y=1 |
|||
|
ƒ0 |
0 | 0 | 0 | 0 | Константа "ноль" | ƒ(x,y)=0 |
|
ƒ1 |
0 | 0 | 0 | 1 | Конъюнкция |
ƒ(x,y)=x&y
ƒ(x,y)=xy |
|
ƒ2 |
0 | 0 | 1 | 0 | Запрет по y | xΔy |
|
ƒ3 |
0 | 0 | 1 | 1 | x | ƒ(x,y)=x |
|
ƒ4 |
0 | 1 | 0 | 0 | Запрет по x | yΔx |
|
ƒ5 |
0 | 1 | 0 | 1 | y | ƒ(x,y)=y |
|
ƒ6 |
0 | 1 | 1 | 0 | Сумма по mod2(неравнозначность) |  |
|
ƒ7 |
0 | 1 | 1 | 1 | Дизъюнкция |
ƒ(x,y)=x v y ƒ(x,y)=x+y |
|
ƒ8 |
1 | 0 | 0 | 0 | Стрелка Пирса (Вебба) |
ƒ(x,y)=x↓y ƒ(x,y)=xОy |
|
ƒ9 |
1 | 0 | 0 | 1 | Равнозначность |
ƒ(x,y)=x≡y ƒ(x,y)=x∞y |
|
ƒ10 |
1 | 0 | 1 | 0 | Инверсия y |
ƒ(x,y)=^y
|
|
ƒ11 |
1 | 0 | 1 | 1 | Импликация от y к x | ƒ(x,y)=y→x |
|
ƒ12 |
1 | 1 | 0 | 0 | Инверсия x |
ƒ(x,y)=^x
|
|
ƒ13 |
1 | 1 | 0 | 1 | Импликация от х к y | ƒ(x,y)=x→y |
|
ƒ14 |
1 | 1 | 1 | 0 | Штрих Шеффера | ƒ(x,y)=x/y |
|
ƒ15 |
1 | 1 | 1 | 1 | Константа "единица" | ƒ(x,y)=1 |
Общее количество функций от n переменных равно: 
Уже на примере этой таблицы, где мы можем перечислить все возможные логические функции от двух переменных, видно, что существуют переменные, от которых ФАЛ меняет свое значение на каких-либо наборах, и переменные, при изменении которое значение функции не меняетсяни на каких наборах переменных.
В первом случае переменную называют фиктивной, а во втором – существенной.
Так, например, для функции ƒ12(x,y) логическая переменная x является существенной, а логическая переменная y – фиктивной.
Рассмотрим теперь логические функции, играющие наибольшую роль в вычислительной технике, и их основные свойства.
