| Россия, Новосибирск |
Ультрафильтры и компактность
Теорема 81. Нестандартный аналог 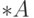 множества
множества  действительных чисел совпадает с
действительных чисел совпадает с  тогда и только тогда, когда множество
тогда и только тогда, когда множество  конечно.
конечно.
Если  конечно, и, скажем, состоит из трех элементов
конечно, и, скажем, состоит из трех элементов 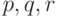 , то можно записать формулу
, то можно записать формулу
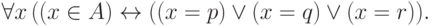
 ,
так что
,
так что 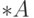 состоит из тех же трех элементов.
состоит из тех же трех элементов.Пусть теперь  бесконечно. Покажем, что
бесконечно. Покажем, что 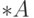 содержит элементы, не входящие в
содержит элементы, не входящие в  . Пусть
. Пусть 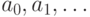 —
последовательность различных элементов множества
—
последовательность различных элементов множества  . Напишем
формулу, которая утверждает, что все элементы этой
последовательности различны и принадлежат
. Напишем
формулу, которая утверждает, что все элементы этой
последовательности различны и принадлежат  . По принципу
переноса все бесконечные члены этой последовательности (точнее,
ее гипердействительного аналога) также различны,
принадлежат
. По принципу
переноса все бесконечные члены этой последовательности (точнее,
ее гипердействительного аналога) также различны,
принадлежат 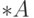 и отличаются от всех конечных членов
последовательности. Они и будут искомыми нестандартными
элементами
и отличаются от всех конечных членов
последовательности. Они и будут искомыми нестандартными
элементами 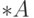 . В самом деле, бесконечный член
. В самом деле, бесконечный член  при бесконечном гипернатуральном
при бесконечном гипернатуральном  не может совпасть с конечными
членами, а также не может совпасть со стандартным элементом
не может совпасть с конечными
членами, а также не может совпасть со стандартным элементом 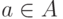 , не входящим в исходную последовательность (ибо
утверждение "
, не входящим в исходную последовательность (ибо
утверждение "  при всех
при всех  " записывается
формулой).
" записывается
формулой).
Галактикой гипердействительного числа  называют
множество всех гипердействительных
называют
множество всех гипердействительных  , для которых разность
, для которых разность  конечна.
конечна.
178. Покажите, что множество гипердействительных чисел разбивается на галактики. Определите на галактиках естественное отношение линейного порядка и покажите, что этот порядок плотный и не имеет наибольшего и наимен
179. Каждое действительное число  , не являющееся двоично-
рациональным, можно единственным образом записать в виде
бесконечной двоичной дроби
, не являющееся двоично-
рациональным, можно единственным образом записать в виде
бесконечной двоичной дроби 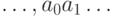 ; другими
словами, ему соответствует последовательность нулей и единиц
(нас будет интересовать лишь дробная часть после запятой).
Фиксируем бесконечное гипернатуральное
; другими
словами, ему соответствует последовательность нулей и единиц
(нас будет интересовать лишь дробная часть после запятой).
Фиксируем бесконечное гипернатуральное  и рассмотрим те
числа
и рассмотрим те
числа  , у которых
, у которых  . Покажите, что множество
таких чисел переходит в свое дополнение при симметрии относительно
любой двоично-рациональной точки (другими словами,
. Покажите, что множество
таких чисел переходит в свое дополнение при симметрии относительно
любой двоично-рациональной точки (другими словами, 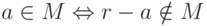 для двоично-рациональных
для двоично-рациональных  ) и потому не может быть измеримым по Лебегу.
\end{problem}
) и потому не может быть измеримым по Лебегу.
\end{problem}
180. Докажите, что гиперрациональными числами являются отношения гиперцелых чисел и только они. Докажите, что каждое гипердействительное число бесконечно близко к некоторому гиперрациональному числу.
Покажем теперь, как можно ввести основные понятия математического анализа, используя бесконечно малые и бесконечно большие числа.
Теорема 82. Пусть 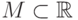 . Множество
. Множество  ограничено (в
обычном смысле) тогда и только тогда, когда все элементы
его гипердействительного аналога конечны.
ограничено (в
обычном смысле) тогда и только тогда, когда все элементы
его гипердействительного аналога конечны.
Таким образом, в курсе нестандартного анализа можно определять ограниченные множества как множества, не содержащие бесконечных элементов.
Если все элементы  меньше некоторого стандартного
меньше некоторого стандартного  по модулю, то и все элементы
по модулю, то и все элементы 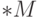 меньше того же
меньше того же  (принцип
переноса), поэтому в одну сторону утверждение очевидно.
(принцип
переноса), поэтому в одну сторону утверждение очевидно.
Пусть теперь  не ограничено (скажем, сверху). Тогда в
не ограничено (скажем, сверху). Тогда в  верно такое утверждение: для всякого
верно такое утверждение: для всякого  найдется элемент
множества
найдется элемент
множества  , больший
, больший  . Применим принцип переноса и
возьмем бесконечно большое
. Применим принцип переноса и
возьмем бесконечно большое  . Получим, что в
. Получим, что в 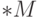 есть
бесконечно большой элемент.
есть
бесконечно большой элемент.
181. Покажите, что если все элементы множества 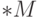 меньше
некоторого гипердействительного
меньше
некоторого гипердействительного  , то
, то  ограничено.
ограничено.
182. Говорят, что множество  гипердействительных чисел является
внутренним, если оно есть гипердействительный аналог
некоторого множества
гипердействительных чисел является
внутренним, если оно есть гипердействительный аналог
некоторого множества  действительных чисел. Покажите, что
множество конечных гипердействительных чисел не является
внутренним.
действительных чисел. Покажите, что
множество конечных гипердействительных чисел не является
внутренним.
183. Докажите, что множество 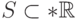 выразимо (в рассматриваемой
нами сигнатуре, содержащей символы для всех функций и предикатов
на множестве
выразимо (в рассматриваемой
нами сигнатуре, содержащей символы для всех функций и предикатов
на множестве  ) тогда и только тогда, когда оно является
внутренним.
) тогда и только тогда, когда оно является
внутренним.
Нестандартный анализ позволяет дать естественные определения предельной точки и предела.
Теорема 83. Число  является предельной точкой
последовательности действительных чисел
является предельной точкой
последовательности действительных чисел 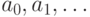 тогда и только тогда, когда найдется
бесконечно далекий член последовательности, бесконечно
близкий к
тогда и только тогда, когда найдется
бесконечно далекий член последовательности, бесконечно
близкий к  .
.
(Бесконечно далеким членом последовательности мы называем значение  при бесконечном гипернатуральном
при бесконечном гипернатуральном  .)
.)
Если  является предельной точкой, то для всякого положительного
является предельной точкой, то для всякого положительного  и всякого натурального
и всякого натурального  найдется натуральное
найдется натуральное  , для которого
, для которого 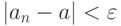 .
Применим принцип переноса, положив
.
Применим принцип переноса, положив  бесконечно малым
и
бесконечно малым
и  бесконечно большим. Получим искомый бесконечно близкий
к
бесконечно большим. Получим искомый бесконечно близкий
к  член с бесконечно большим гипернатуральным номером.
член с бесконечно большим гипернатуральным номером.
Напротив, если для некоторого натурального  и для некоторого
и для некоторого  все члены последовательности, начиная с
все члены последовательности, начиная с  -го, отстоят от
-го, отстоят от  более чем на
более чем на  , то по
принципу переноса все бесконечно далекие члены последовательности также
отстоят от
, то по
принципу переноса все бесконечно далекие члены последовательности также
отстоят от  более чем на
более чем на  .
.
184. Покажите, что число  принадлежит замыканию множества
принадлежит замыканию множества 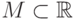 тогда и только тогда, когда некоторый элемент
множества
тогда и только тогда, когда некоторый элемент
множества 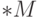 бесконечно близок к
бесконечно близок к  .
.
185. Как определить в терминах нестандартного анализа понятие предельной точки множества (в любой окрестности которой бесконечно много членов множества)?
Теперь видно, что нестандартный анализ позволяет в два счета доказать теорему о том, что всякая ограниченная последовательность имеет предельную точку: в самом деле, любой бесконечно далекий член этой последовательности конечен, и его стандартная часть будет предельной точкой!
Теорем 84. Последовательность 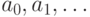 действительных чисел сходится
к числу
действительных чисел сходится
к числу  тогда и только тогда, когда все ее бесконечно далекие
члены бесконечно близки к
тогда и только тогда, когда все ее бесконечно далекие
члены бесконечно близки к  .
.
Пусть  является пределом. Тогда для всякого
является пределом. Тогда для всякого  найдется
найдется  , начиная с которого все члены последовательности
отстоят от
, начиная с которого все члены последовательности
отстоят от  менее чем на
менее чем на  . В частности,
все бесконечно далекие члены таковы и их расстояние до
. В частности,
все бесконечно далекие члены таковы и их расстояние до  меньше
любого стандартного
меньше
любого стандартного  .
.
Напротив, пусть  не является пределом и для
всякого
не является пределом и для
всякого  найдется член
найдется член 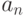 с номером
с номером  , отстоящий
от
, отстоящий
от  более чем на
более чем на 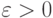 (пока что все параметры стандартны).
Применим принцип переноса, взяв
(пока что все параметры стандартны).
Применим принцип переноса, взяв  бесконечно большим,
и найдем бесконечно далекий член последовательности,
отстоящий от
бесконечно большим,
и найдем бесконечно далекий член последовательности,
отстоящий от  более чем на стандартное
более чем на стандартное 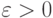 .
.
Приведем теперь нестандартные критерии стандартных топологических понятий.
Теорема 85. Множество 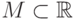 открыто
тогда и только тогда, когда вместо со всякой точкой
открыто
тогда и только тогда, когда вместо со всякой точкой  оно содержит
и всю ее монаду, то есть все гипердействительные точки,
бесконечно близкие к
оно содержит
и всю ее монаду, то есть все гипердействительные точки,
бесконечно близкие к  .
.
(Cтрого говоря, следовало бы сказать "его нестандартный аналог 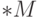 " вместо "оно";
напомним также, что
" вместо "оно";
напомним также, что  и
и 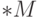 содержат одни и те же
стандартные числа.)
содержат одни и те же
стандартные числа.)
Если  открыто и содержит вместе с точкой
открыто и содержит вместе с точкой  ее
ее  -окрестность, то монада точки
-окрестность, то монада точки  по
принципу переноса содержится в
по
принципу переноса содержится в  .
.
Если же некоторая точка  не является
внутренней и для всякого действительного
не является
внутренней и для всякого действительного 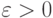 найдется точка вне
найдется точка вне  на расстоянии меньше
на расстоянии меньше  , применим принцип переноса и возьмем бесконечно малое
, применим принцип переноса и возьмем бесконечно малое  . Мы получим число, бесконечно близкое к
. Мы получим число, бесконечно близкое к  и не лежащее в
и не лежащее в 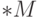 .
.
Переходя к дополнениям, получаем, что множество 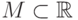 замкнуто тогда и только тогда, когда любая стандартная точка,
бесконечно близкая к некоторой точке из
замкнуто тогда и только тогда, когда любая стандартная точка,
бесконечно близкая к некоторой точке из 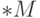 , принадлежит
, принадлежит  .
.
На прямой компактными являются замкнутые ограниченные множества. Соединим нестандартные критерии замкнутости и ограниченности:
