| Россия, Новосибирск |
Ультрафильтры и компактность
Нестандартный анализ
Один из создателей теории моделей, А.Робинсон, заметил, что с ее помощью можно придать точный смысл понятиям "бесконечно малых" и "бесконечно больших" величин, с которыми оперировали еще Ньютон и Лейбниц и которые затем были изгнаны и заменены рассуждениями с эпсилонами и дельтами.
Это направление получило название нестандартного анализа. Целей тут две: во-первых, упростить доказательства известных теорем, во-вторых, использовать методы нестандартного анализа для получения новых результатов. Насколько эти цели достигнуты за тридцать с лишним лет, прошедших с возникновения нестандартного анализа?
Простота доказательств — дело вкуса. Конечно, всякий преподаватель курса математического анализа мечтает избавиться от утомительных рассуждений с выбором достаточно малых эпсилонов. Но если вместо этого нужно постоянно переходить от модели к ее элементарному расширению и обратно, лекарство может оказаться страшнее болезни. Во всяком случае, " нестандартные" учебники математического анализа для нематематиков (один из них написан Кейслером [34]) большого распространения не получили.
Новые результаты действительно были получены; отметим, что многие из них (хотя и не все) впоследствии были передоказаны "стандартными" методами, так что и здесь революции не произошло.
Так или иначе, нестандартный анализ — интересное приложение теории моделей, и мы разберем несколько простых примеров. Более подробно об этом можно прочесть в книгах Дэвиса [11] и Успенского [27], а также в последней главе книги Робинсона [22].
Идея нестандартного анализа проста. Среди действительных чисел,
увы, нет бесконечно малых (которые были бы меньше 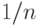 при всех
при всех 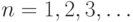 ) — как говорят, поле вещественных чисел
удовлетворяет аксиоме Архимеда. (Оригинальная формулировка этой аксиомы: каковы бы ни были два отрезка, можно
отложить меньший из них столько раз, чтобы превзойти больший.)
Но можно рассмотреть элементарное расширение поля
) — как говорят, поле вещественных чисел
удовлетворяет аксиоме Архимеда. (Оригинальная формулировка этой аксиомы: каковы бы ни были два отрезка, можно
отложить меньший из них столько раз, чтобы превзойти больший.)
Но можно рассмотреть элементарное расширение поля  ,
в котором такие бесконечно малые элементы есть, и использовать
их для определения пределов, производных и прочего в исходном поле.
,
в котором такие бесконечно малые элементы есть, и использовать
их для определения пределов, производных и прочего в исходном поле.
Перейдем к формальным определениям. Мы будет рассматривать
вещественную прямую как модель очень богатой сигнатуры. Для
каждого отношения на  (c произвольным числом аргументов)
введем свой предикатный символ. Получится
(c произвольным числом аргументов)
введем свой предикатный символ. Получится 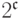 предикатных символов. Кроме того, для каждой функции из
предикатных символов. Кроме того, для каждой функции из 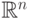 в
в  (при всех
(при всех 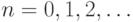 ) введем свой
функциональный символ. Это даст еще
) введем свой
функциональный символ. Это даст еще 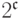 символов.
символов.
Пусть  — любая нормальная интерпретация этой сигнатуры,
элементарно эквивалентная
— любая нормальная интерпретация этой сигнатуры,
элементарно эквивалентная  . Ее можно считать полем,
расширяющим поле
. Ее можно считать полем,
расширяющим поле  . В самом деле, среди функциональных
символов есть двуместные символы для сложения и умножения. Они
задают некоторые операции в
. В самом деле, среди функциональных
символов есть двуместные символы для сложения и умножения. Они
задают некоторые операции в  и относительно этих операций
множество
и относительно этих операций
множество  будет полем, так как аксиомы поля можно
записать в виде формул (эти формулы истинны в
будет полем, так как аксиомы поля можно
записать в виде формул (эти формулы истинны в  , а потому и
в
, а потому и
в 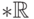 ). Аналогичное рассуждение с предикатом "меньше"
показывает, что
). Аналогичное рассуждение с предикатом "меньше"
показывает, что 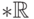 является упорядоченным полем.
является упорядоченным полем.
Это поле можно считать расширением поля  . В самом деле,
для каждого действительного числа
. В самом деле,
для каждого действительного числа  в сигнатуре имеется
константа. Значения таких констант образуют подполе в
в сигнатуре имеется
константа. Значения таких констант образуют подполе в  ,
изоморфное
,
изоморфное  . В самом деле, утверждения вида
. В самом деле, утверждения вида 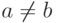 ,
, 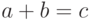 и
и 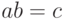 являются формулами, и переносятся
из
являются формулами, и переносятся
из  в
в  . Аналогичным образом это вложение
сохраняет порядок.
. Аналогичным образом это вложение
сохраняет порядок.
Если поле  исчерпывается значениями констант
из
исчерпывается значениями констант
из  ,то ничего интересного не получается. Поэтому мы будем
предполагать, что это не так. Возможность построить
,то ничего интересного не получается. Поэтому мы будем
предполагать, что это не так. Возможность построить  , не
совпадающее с
, не
совпадающее с  , следует (например) из теоремы Левенгейма-
Сколема о повышении мощности. Другой способ: добавим в сигнатуру
новую константу
, следует (например) из теоремы Левенгейма-
Сколема о повышении мощности. Другой способ: добавим в сигнатуру
новую константу  и рассмотрим теорию
и рассмотрим теорию
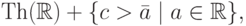
 — множество всех истинных в
— множество всех истинных в  формул нашей сигнатуры, а
формул нашей сигнатуры, а  — константа для числа
— константа для числа  .
Совместность этой теории следует из теоремы компактности.
Любая ее модель годится в качестве
.
Совместность этой теории следует из теоремы компактности.
Любая ее модель годится в качестве  , поскольку значение
константы
, поскольку значение
константы  больше всех элементов из
больше всех элементов из  .
.164. Проведите это рассуждение подробно.
В дальнейшем мы предполагаем, что выбрана и зафиксирована
некоторая интерпретация 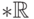 , являющаяся элементарным
расширением
, являющаяся элементарным
расширением  и не совпадающая с
и не совпадающая с  . Ее
элементы мы называем гипердействительными числами.
Среди них есть и действительные числа, которые мы будем называть
также стандартными элементами
. Ее
элементы мы называем гипердействительными числами.
Среди них есть и действительные числа, которые мы будем называть
также стандартными элементами  . Остальные элементы
. Остальные элементы  будут нестандартными гипердействительными числами. (По нашему предположению таковые существуют.)
будут нестандартными гипердействительными числами. (По нашему предположению таковые существуют.)
Утверждение об элементарной эквивалентности  и
и  называют принципом переноса:
он позволяет перенести истинность формулы из
называют принципом переноса:
он позволяет перенести истинность формулы из  в
в  (или
наоборот).
(или
наоборот).
Возможность переноса не ограничивается алгебраическими
свойствами. Например, в нашей сигнатуре есть функция  . В
интерпретации
. В
интерпретации  ей соответствует функция, которую можно
было бы назвать "гипердействительным синусом". Эта функция
продолжает обычный синус (для стандартных аргументов), поскольку
утверждения вида
ей соответствует функция, которую можно
было бы назвать "гипердействительным синусом". Эта функция
продолжает обычный синус (для стандартных аргументов), поскольку
утверждения вида 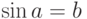 для конкретных
стандартных
для конкретных
стандартных  и
и  можно перенести в
можно перенести в  . Более того, она обладает
обычными свойствами синуса: скажем, гипердействительный синус
любого гипердействительного числа не превосходит единицы (в
смысле порядка на
. Более того, она обладает
обычными свойствами синуса: скажем, гипердействительный синус
любого гипердействительного числа не превосходит единицы (в
смысле порядка на  ), поскольку формула
), поскольку формула  выдерживает перенос. Аналогично можно поступать и с
предикатами: например, предикат "быть натуральным числом"
задает в
выдерживает перенос. Аналогично можно поступать и с
предикатами: например, предикат "быть натуральным числом"
задает в  некоторое подмножество, элементы которого
естественно назвать гипернатуральными числами. Гипернатуральные
числа делятся на стандартные (соответствующие обычным натуральным
числам в
некоторое подмножество, элементы которого
естественно назвать гипернатуральными числами. Гипернатуральные
числа делятся на стандартные (соответствующие обычным натуральным
числам в  ) и нестандартные. (Мы увидим, что нестандартные
числа обязательно найдутся.) Множество гипернатуральных чисел
обозначается
) и нестандартные. (Мы увидим, что нестандартные
числа обязательно найдутся.) Множество гипернатуральных чисел
обозначается 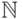 .
.
Аналогично определяется множество 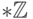 гиперцелых
чисел и вообще множество
гиперцелых
чисел и вообще множество 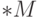 для любого множества
для любого множества  действительных чисел. (Множеству
действительных чисел. (Множеству  соответствует одноместный
предикатный символ;
соответствует одноместный
предикатный символ; 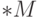 — интерпретация этого символа в
— интерпретация этого символа в  .) Множество
.) Множество 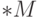 называют нестандартным
расширением
называют нестандартным
расширением  . В нем содержатся те же стандартные числа, что и
в
. В нем содержатся те же стандартные числа, что и
в  (формулы вида
(формулы вида  для стандартных
чисел
для стандартных
чисел  переносятся), и, возможно, некоторые нестандартные числа.
переносятся), и, возможно, некоторые нестандартные числа.
Принцип переноса гарантирует, что для конечного  нестандартных элементов в
нестандартных элементов в 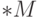 не появится. В самом деле,
пусть, скажем, в
не появится. В самом деле,
пусть, скажем, в  ровно три элемента
ровно три элемента  ,
,  и
и  . Тогда
формула
. Тогда
формула
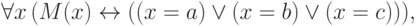
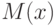 — предикат, соответствующий
множеству
— предикат, соответствующий
множеству  , истинна в
, истинна в  . По принципу переноса она истинна и в
. По принципу переноса она истинна и в  , так что и
, так что и 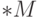 состоит из трех элементов, являющихся
значениями констант
состоит из трех элементов, являющихся
значениями констант  ,
,  и
и  (отождествленных со стандартными действительными числами).
(отождествленных со стандартными действительными числами).Впоследствии мы увидим, что бесконечное множество  обязательно приобретет новые нестандартные элементы при переходе
к
обязательно приобретет новые нестандартные элементы при переходе
к  .
.
Несколько простых следствий принципа переноса:

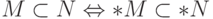 (применяем принцип переноса к формуле
(применяем принцип переноса к формуле  );
); , (применяем принцип переноса к формуле
, (применяем принцип переноса к формуле 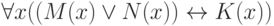 , где
, где  — объединение
— объединение  );
);