| Россия |
Контроль функции выходов неинициального автомата с использованием простого безусловного эксперимента
Рассмотрим следующую задачу. Пусть в распоряжении экспериментатора имеется один экземпляр автомата Мили  , у которого известны входной алфавит
, у которого известны входной алфавит  , выходной алфавит
, выходной алфавит 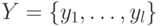 , множество состояний
, множество состояний 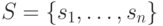 , функция переходов
, функция переходов  . Требуется построить простой безусловный эксперимент, позволяющий распознать функцию выходов
. Требуется построить простой безусловный эксперимент, позволяющий распознать функцию выходов  автомата
автомата  или эквивалентного ему автомата. Эта задача отличается от задачи, сформулированной в лекции 6, лишь тем, что рассматриваемый здесь автомат предполагается неинициальным. Вследствие тех же причин, которые были приведены в лекции 6, содержательный смысл рассматриваемой задачи, в частности, соответствует и контролю функции выходов неинициального автомата.
или эквивалентного ему автомата. Эта задача отличается от задачи, сформулированной в лекции 6, лишь тем, что рассматриваемый здесь автомат предполагается неинициальным. Вследствие тех же причин, которые были приведены в лекции 6, содержательный смысл рассматриваемой задачи, в частности, соответствует и контролю функции выходов неинициального автомата.
Следующая теорема описывает класс автоматов, для которого сформулированная задача разрешима.
Теорема 7.1. Для того чтобы задача распознавания функции выходов неинициального автомата (с точностью до эквивалентности) была разрешима, необходимо и достаточно, чтобы автомат был сильно связен.
Необходимость условия теоремы является очевидной, поэтому остановимся лишь на доказательстве его достаточности.
Достаточность. Построим всевозможные таблицы размерности  , состоящие из элементов множества
, состоящие из элементов множества  . Число таких таблиц конечно и равно
. Число таких таблиц конечно и равно  . Очевидно, что класс автоматов
. Очевидно, что класс автоматов  , у которых функция переходов совпадает с
, у которых функция переходов совпадает с  , содержит автомат
, содержит автомат  . Среди автоматов класса
. Среди автоматов класса  встречаются попарно эквивалентные. Из каждого множества всех эквивалентных автоматов произвольным образом выбираем по одному представителю и образуем из них новый класс автоматов
встречаются попарно эквивалентные. Из каждого множества всех эквивалентных автоматов произвольным образом выбираем по одному представителю и образуем из них новый класс автоматов 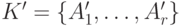 , где
, где  . По построению в классе
. По построению в классе  отсутствуют попарно эквивалентные автоматы, а один из автоматов
отсутствуют попарно эквивалентные автоматы, а один из автоматов  совпадает с автоматом
совпадает с автоматом  или ему эквивалентен.
или ему эквивалентен.
По предположению каждый  является сильно связным, но тогда можно показать, что построенный нами класс автоматов
является сильно связным, но тогда можно показать, что построенный нами класс автоматов  является исключительным. Известно [18], что исключительность класса является необходимым и достаточным условием распознаваемости автомата, принадлежащего этому классу, простым безусловным экспериментом. Таким образом, исходная задача сведена к задаче распознавания автомата, принадлежащего известному классу, которая в нашем случае оказывается разрешимой. Этим и заканчивается доказательство теоремы.
является исключительным. Известно [18], что исключительность класса является необходимым и достаточным условием распознаваемости автомата, принадлежащего этому классу, простым безусловным экспериментом. Таким образом, исходная задача сведена к задаче распознавания автомата, принадлежащего известному классу, которая в нашем случае оказывается разрешимой. Этим и заканчивается доказательство теоремы.
Из приведенного доказательства следует применимость метода (предложенного в [18]) распознавания автомата, принадлежащего известному классу, к решению рассматриваемой нами задачи. Однако в этом случае он обладает тем недостатком, что при больших 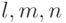 число автоматов в классе
число автоматов в классе  велико, что вызывает значительное увеличение длины соответствующего эксперимента.
велико, что вызывает значительное увеличение длины соответствующего эксперимента.
В связи со сказанным мы рассмотрим иной способ проведения эксперимента, позволяющий сократить мощность рассматриваемого класса автоматов и упростить сам эксперимент. Предположим, что исследуемый неинициальный автомат  находится в состоянии
находится в состоянии 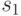 . Построим для автомата
. Построим для автомата  характеристическое слово, которое обозначим через
характеристическое слово, которое обозначим через 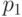 , и подадим его на вход исследуемого автомата.
, и подадим его на вход исследуемого автомата.
По наблюдаемой реакции  решаем задачу распознавания функции выходов
решаем задачу распознавания функции выходов 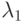 автомата Мили, которому соответствует автомат без выходов
автомата Мили, которому соответствует автомат без выходов  . Вообще говоря, эта задача может и не иметь решения из-за неоднозначности, возникающей в процессе построения
. Вообще говоря, эта задача может и не иметь решения из-за неоднозначности, возникающей в процессе построения 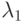 . Неоднозначность этой функции означает, что
. Неоднозначность этой функции означает, что 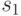 заведомо не является истинным начальным состоянием исследуемого автомата
заведомо не является истинным начальным состоянием исследуемого автомата  . Если же задача разрешима, то обозначим через
. Если же задача разрешима, то обозначим через 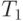 таблицу, которая соответствует распознанной функции выходов
таблицу, которая соответствует распознанной функции выходов 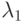 .
.
Предположим далее, что начальным состоянием исследуемого автомата перед подачей слова 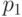 было
было 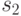 . Рассмотрим автомат
. Рассмотрим автомат  и найдем такое слово
и найдем такое слово 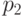 , чтобы
, чтобы 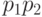 являлось для
являлось для  характеристическим словом. В частности, в качестве
характеристическим словом. В частности, в качестве 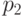 можно взять характеристическое слово для автомата
можно взять характеристическое слово для автомата 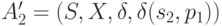 . Подаем
. Подаем 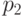 на вход исследуемого автомата, и пусть наблюдаемая его реакция есть
на вход исследуемого автомата, и пусть наблюдаемая его реакция есть  . По реакции
. По реакции  решаем задачу распознавания функции выходов
решаем задачу распознавания функции выходов 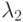 автомата Мили, которому соответствует автомат без выходов
автомата Мили, которому соответствует автомат без выходов  . Если эта задача разрешима, то обозначим через
. Если эта задача разрешима, то обозначим через 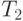 таблицу, которая соответствует распознанной функции выходов
таблицу, которая соответствует распознанной функции выходов 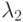 .
.
Продолжая этот процесс и далее аналогичным образом в предположении, что начальным состоянием исследуемого автомата перед подачей слова 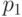 были состояния
были состояния 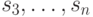 соответственно, строим, если задачи оказываются разрешимыми, таблицы
соответственно, строим, если задачи оказываются разрешимыми, таблицы 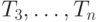 , представляющие собой распознанные функции выходов
, представляющие собой распознанные функции выходов  .
.
Предположим, что в результате описанного процесса построены таблицы  , где
, где  . Рассмотрим класс автоматов
. Рассмотрим класс автоматов  , функции переходов которых совпадают с функцией переходов
, функции переходов которых совпадают с функцией переходов  исследуемого автомата, а функции выходов заданы упомянутыми таблицами. Легко видеть, что по крайней мере один из автоматов класса
исследуемого автомата, а функции выходов заданы упомянутыми таблицами. Легко видеть, что по крайней мере один из автоматов класса  совпадает с исследуемым автоматом или ему эквивалентен. Может оказаться, что в классе
совпадает с исследуемым автоматом или ему эквивалентен. Может оказаться, что в классе  есть попарно эквивалентные автоматы. В этом случае из каждого множества всех эквивалентных автоматов выберем по одному представителю с наибольшим номером и образуем из них новый класс
есть попарно эквивалентные автоматы. В этом случае из каждого множества всех эквивалентных автоматов выберем по одному представителю с наибольшим номером и образуем из них новый класс  .
.
Поскольку все автоматы из  являются сильно связными, а по построению - попарно эквивалентными, то из уже приводимого выше утверждения [18] следует, что класс
являются сильно связными, а по построению - попарно эквивалентными, то из уже приводимого выше утверждения [18] следует, что класс  исключительный. Отметим, что при больших
исключительный. Отметим, что при больших 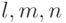 мощность
мощность  меньше мощности класса
меньше мощности класса  , рассматриваемого в методе из [18].
, рассматриваемого в методе из [18].
Предположим, что автомат 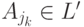 был выбран из класса
был выбран из класса  в качестве представителя множества эквивалентных автоматов
в качестве представителя множества эквивалентных автоматов 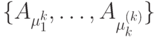 , где
, где 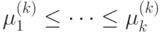 и
и  . Пусть
. Пусть 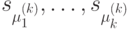 - состояния исследуемого автомата
- состояния исследуемого автомата  , в которых он находился по предположению при построении таблиц
, в которых он находился по предположению при построении таблиц  соответственно. Образуем множество состояний
соответственно. Образуем множество состояний
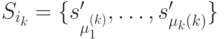
где 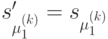 , а состояние
, а состояние 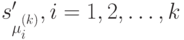 , есть состояние автомата
, есть состояние автомата  , эквивалентное
, эквивалентное 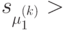 . Если в
. Если в  существует несколько состояний, эквивалентных
существует несколько состояний, эквивалентных  , то в качестве
, то в качестве 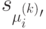 произвольным образом выбираем одно из них. Построим теперь множество состояний
произвольным образом выбираем одно из них. Построим теперь множество состояний
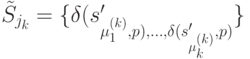
где  - слово, использованное на предыдущем этапе эксперимента для построения автоматов класса
- слово, использованное на предыдущем этапе эксперимента для построения автоматов класса  . Образуем, наконец, множество состояний
. Образуем, наконец, множество состояний  .
.
Рассмотрим теперь автомат  , состоящий из изолированных подавтоматов
, состоящий из изолированных подавтоматов  и по терминологии [18] называемый расщепляемым. Из приведенных выше построений вытекает, что исследуемый автомат совпадает с одним из подавтоматов
и по терминологии [18] называемый расщепляемым. Из приведенных выше построений вытекает, что исследуемый автомат совпадает с одним из подавтоматов  , находящимся в данный момент в одном из состояний множества
, находящимся в данный момент в одном из состояний множества  , либо ему эквивалентен. Для завершения эксперимента по распознаванию исследуемого автомата достаточно для расщепляемого автомата
, либо ему эквивалентен. Для завершения эксперимента по распознаванию исследуемого автомата достаточно для расщепляемого автомата 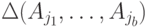 с множеством допустимых начальных состояний
с множеством допустимых начальных состояний  построить такое слово
построить такое слово 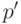 , реакция на которое позволяет определить, к какому из изолированных подавтоматов принадлежит конечное состояние. Очевидно, что этот подавтомат и является искомым.
, реакция на которое позволяет определить, к какому из изолированных подавтоматов принадлежит конечное состояние. Очевидно, что этот подавтомат и является искомым.
Эта задача, как нетрудно видеть, является обобщенной задачей установки, рассмотренной в [63]. Напомним, что слово  называется "обобщенным" установочным словом для автомата
называется "обобщенным" установочным словом для автомата  и пары
и пары  , если
, если
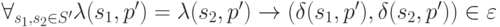
где 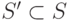 - некоторое выделенное подмножество состояний автомата
- некоторое выделенное подмножество состояний автомата  , интерпретируемое как множество допустимых начальных состояний
, интерпретируемое как множество допустимых начальных состояний  , а
, а 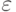 - некоторое отношение эквивалентности на множестве
- некоторое отношение эквивалентности на множестве  , классы которого определяют "точность" решения задачи установки. Если
, классы которого определяют "точность" решения задачи установки. Если 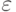 есть тождественное отношение, то "обобщенная" задача установки вырождается в обычную задачу установки.
есть тождественное отношение, то "обобщенная" задача установки вырождается в обычную задачу установки.
Применительно к нашему случаю рассмотрим "обобщенную" установочную задачу, когда 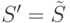 , а классами отношения
, а классами отношения 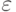 являются множества состояний изолированных подавтоматов
являются множества состояний изолированных подавтоматов 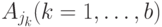 .
.
В [63] показано, что условие
 |
( 7.1) |
является достаточным для существования "обобщенного" установочного слова для автомата 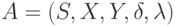 , где бинарное отношение
, где бинарное отношение 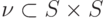 определяется следующим образом:
определяется следующим образом:

Выше показано, что класс автоматов  является исключительным. Из этого следует, что в рассматриваемом нами случае условие (7.1) выполняется. Таким образом, знания реакции исследуемого автомата на "обобщенное" установочное слово
является исключительным. Из этого следует, что в рассматриваемом нами случае условие (7.1) выполняется. Таким образом, знания реакции исследуемого автомата на "обобщенное" установочное слово 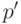 достаточно для определения того изолированного подавтомата
достаточно для определения того изолированного подавтомата  расщепляемого автомата
расщепляемого автомата 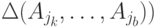 , которому принадлежит конечное состояние.
, которому принадлежит конечное состояние.
Итак, нами построен и обоснован алгоритм распознавания функции выходов неинициального автомата, который является более эффективным с точки зрения уменьшения объема вычислений, чем алгоритм Гилла [18].
Перейдем теперь к установлению верхней оценки длины описанного эксперимента, включающего в себя подачу на вход исследуемого автомата слова  и "обобщенного" установочного слова
и "обобщенного" установочного слова 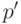 .
.
Поскольку слово 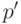 является по построению характеристическим для автомата
является по построению характеристическим для автомата  , то из (6.7) следует, что длина его не превосходит величины
, то из (6.7) следует, что длина его не превосходит величины 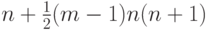 , где
, где 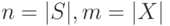 . Длина слов
. Длина слов  тем более не превосходит этой величины. Тогда длина слова
тем более не превосходит этой величины. Тогда длина слова  не превосходит величины
не превосходит величины ![n[n+\frac12(m-1)n(n+1)]](/sites/default/files/tex_cache/6cc2f162b8ddce900e692e38266c8cd9.png) .
.
Слово 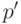 является "обобщенным" установочным словом для автомата
является "обобщенным" установочным словом для автомата 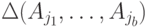 , число состояний которого не больше
, число состояний которого не больше 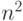 , а мощность множества допустимых начальных состояний не превышает
, а мощность множества допустимых начальных состояний не превышает  . Очевидно, что длина слова
. Очевидно, что длина слова 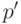 не превышает длины установочного слова для того же автомата, понимаемого в обычном смысле. Тогда в силу результатов, полученных в [67], верхняя оценка длины
не превышает длины установочного слова для того же автомата, понимаемого в обычном смысле. Тогда в силу результатов, полученных в [67], верхняя оценка длины 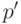 есть
есть 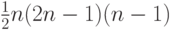 . Как следствие, из наших рассуждений вытекает следующее утверждение.
. Как следствие, из наших рассуждений вытекает следующее утверждение.
Теорема 7.2. Длина кратчайшего простого безусловного эксперимента, позволяющего распознавать функцию выходов сильно связного неинициального автомата 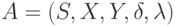 , где
, где  , не превышает величины
, не превышает величины

Проиллюстрируем построение эксперимента на примере. Рассмотрим автомат  , функция переходов которого задана в табл. 7.1. Пусть его истинное начальное состояние (неизвестное экспериментатору) есть
, функция переходов которого задана в табл. 7.1. Пусть его истинное начальное состояние (неизвестное экспериментатору) есть 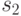 . В предположении, что начальным состоянием автомата
. В предположении, что начальным состоянием автомата  является
является 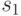 , строим характеристическое слово
, строим характеристическое слово  .
.
Пусть реакция автомата  на
на 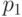 есть слово 1001100. Предполагаемые переходы и наблюдаемая реакция
есть слово 1001100. Предполагаемые переходы и наблюдаемая реакция  ) позволяют построить таблицу выходов
) позволяют построить таблицу выходов 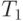 . Истинные переходы автомата
. Истинные переходы автомата  при подаче слова
при подаче слова 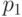 таковы:
таковы:
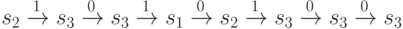
Далее, в предположении, что начальным состоянием  было
было 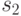 , строим слово
, строим слово  , позволяющее обойти дуги графа автомата
, позволяющее обойти дуги графа автомата  , не пройденные при подаче слова
, не пройденные при подаче слова 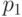 . При этом предполагаемые и истинные переходы такие:
. При этом предполагаемые и истинные переходы такие:

Наблюдаемая реакция  на слово
на слово 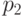 дает возможность завершить заполнение таблицы
дает возможность завершить заполнение таблицы 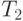 . Предположим теперь, что начальным состоянием
. Предположим теперь, что начальным состоянием  было
было  . Тогда переходы
. Тогда переходы  при подаче на вход слова
при подаче на вход слова 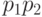 должны иметь вид
должны иметь вид

Из приведенной цепочки видно, что записи в таблице  , соответствующие состояниям
, соответствующие состояниям 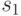 при входе 0 и
при входе 0 и  при входе 1, будут противоречивыми. Это означает, что
при входе 1, будут противоречивыми. Это означает, что  не может являться начальным состоянием
не может являться начальным состоянием  . Таким образом, рассматриваемый автомат
. Таким образом, рассматриваемый автомат  совпадает (или эквивалентен) с автоматом
совпадает (или эквивалентен) с автоматом  , функция выходов которого задана табл. 7.2, либо с автоматом
, функция выходов которого задана табл. 7.2, либо с автоматом  , функция выходов которого задана табл.7.3.
, функция выходов которого задана табл.7.3.
Множество  в рассматриваемом случае есть
в рассматриваемом случае есть 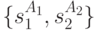 . Установочной последовательностью для расщепляемого автомата
. Установочной последовательностью для расщепляемого автомата  является, например, 0. При подаче на вход автомата
является, например, 0. При подаче на вход автомата  символа 0 пусть его реакция есть 1, т. е. конечным состоянием автомата
символа 0 пусть его реакция есть 1, т. е. конечным состоянием автомата  является
является 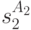 . Отсюда следует, что рассматриваемый автомат
. Отсюда следует, что рассматриваемый автомат  совпадает с
совпадает с  или эквивалентен ему.
или эквивалентен ему.
Приведем теперь некоторые соображения, сокращающие длину эксперимента. Такое сокращение возможно, например, когда у рассматриваемого автомата 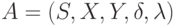 существует слово
существует слово 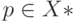 , такое, что
, такое, что  , где
, где  . В этом случае после подачи слова
. В этом случае после подачи слова  на вход автомата число его допустимых начальных состояний уменьшается и, соответственно, уменьшается число таблиц
на вход автомата число его допустимых начальных состояний уменьшается и, соответственно, уменьшается число таблиц 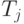 , которые необходимо строить в процессе проведения эксперимента. Отсюда возникает задача отыскания для заданного автомата
, которые необходимо строить в процессе проведения эксперимента. Отсюда возникает задача отыскания для заданного автомата  такого слова
такого слова  , чтобы
, чтобы  была минимальной.
была минимальной.
Эта задача может быть решена с использованием конструкции синхронизирующего дерева для алфавита  , описанной в лекции 1. Каждый лист этого дерева связан с некоторой
, описанной в лекции 1. Каждый лист этого дерева связан с некоторой  -группой. При этом ее мощность может равняться либо 1, что говорит о наличии у автомата
-группой. При этом ее мощность может равняться либо 1, что говорит о наличии у автомата  синхронизирующей последовательности, либо некоторому числу
синхронизирующей последовательности, либо некоторому числу  .
.
В последнем случае путь, ведущий из вершины синхронизирующего дерева в эту  -группу, не соответствует входной последовательности, являющейся синхронизирующей. Среди
-группу, не соответствует входной последовательности, являющейся синхронизирующей. Среди  -групп упомянутого дерева, связанных с его конечными ветвями, т. е. листьями, найдем такую, число элементов которой минимально. Заметим, что, вообще говоря, таких
-групп упомянутого дерева, связанных с его конечными ветвями, т. е. листьями, найдем такую, число элементов которой минимально. Заметим, что, вообще говоря, таких  -групп может быть несколько. Простые рассуждения показывают, что слово
-групп может быть несколько. Простые рассуждения показывают, что слово  , которое соответствует пути по дереву, ведущему из корня к ветви, связанной с минимальной по мощности
, которое соответствует пути по дереву, ведущему из корня к ветви, связанной с минимальной по мощности  -группой, дает решение поставленной задачи.
-группой, дает решение поставленной задачи.
Вернемся к рассмотренному выше примеру. Выполнив для автомата  построения синхронизирующего дерева, находим, что слово
построения синхронизирующего дерева, находим, что слово 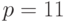 является для него синхронизирующей последовательностью. После подачи его на вход автомат устанавливается в состояние
является для него синхронизирующей последовательностью. После подачи его на вход автомат устанавливается в состояние 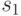 , и завершающий этап эксперимента таким образом сводится к подаче на автомат слова
, и завершающий этап эксперимента таким образом сводится к подаче на автомат слова 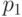 , являющегося характеристическим для
, являющегося характеристическим для  в состоянии
в состоянии 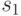 . Общая длина эксперимента при этом равна 9, тогда как длина построенного ранее эксперимента была равна 12.
. Общая длина эксперимента при этом равна 9, тогда как длина построенного ранее эксперимента была равна 12.
Вопросы и упражнения
- Сформулируйте постановку задачи контроля функции выходов неинициального автомата.
- Каков критерий разрешимости этой задачи?
- К какой классической задаче сводится исследуемая здесь задача?
- Опишите процедуру решения соответствующей классической задачи.
- Сформулируйте "обобщенную" установочную задачу и приведите достаточное условие ее разрешимости.
- Приведите верхнюю оценку длины эксперимента, контролирующего функцию выхода неинициального автомата. Является ли эта оценка достижимой?

