| Россия |
Преобразования автоматов в автоматы без потери информации
Рассмотрим проверочный граф 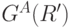 автомата
автомата 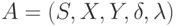 , где
, где  - регулярное выражение события
- регулярное выражение события  . Выделим все слова
. Выделим все слова  из
из  , такие, что соответствующие им пути в графе
, такие, что соответствующие им пути в графе 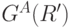 содержат выделенные дуги, исходящие из вершины типа
содержат выделенные дуги, исходящие из вершины типа 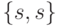 , а также дуги, заходящие в вершину такого же типа. Множество всех таких путей обозначим через
, а также дуги, заходящие в вершину такого же типа. Множество всех таких путей обозначим через  . Легко видеть, что множество всех путей
. Легко видеть, что множество всех путей  и множество выделенных дуг
и множество выделенных дуг  принадлежат
принадлежат  : все пути из
: все пути из  , не совпадающие с путями из
, не совпадающие с путями из  и
и  , содержат их в качестве отрезков.
, содержат их в качестве отрезков.
Отсюда следует, что если в графе 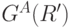 отсутствуют пути из множеств
отсутствуют пути из множеств  и
и  , то и пути из множества
, то и пути из множества  в нем также отсутствуют. Таким образом, из теоремы 5.2 вытекает, что для преобразования автомата
в нем также отсутствуют. Таким образом, из теоремы 5.2 вытекает, что для преобразования автомата  в
в  -БПИ-автомат достаточно из графа
-БПИ-автомат достаточно из графа 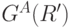 удалить все пути множества
удалить все пути множества  и все выделенные дуги множества
и все выделенные дуги множества  .
.
Перейдем к рассмотрению алгоритма, позволяющего по множествам  и
и  строить такое множество
строить такое множество  дуг графа
дуг графа 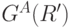 , чтобы после их удаления из этого графа в нем отсутствовали все пути из
, чтобы после их удаления из этого графа в нем отсутствовали все пути из  и все дуги из
и все дуги из  .
.
Алгоритм выбора множества дуг  можно сформулировать следующим образом.
можно сформулировать следующим образом.
Полагаем  , где
, где  - множество выделенных дуг графа
- множество выделенных дуг графа 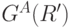 , каждая из которых соединяет вершины типа
, каждая из которых соединяет вершины типа 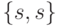 . Если
. Если  , то перейти к пункту 2, иначе к пункту 4.
, то перейти к пункту 2, иначе к пункту 4.
- Из множества
 выделяем множество
выделяем множество 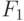 всех дуг, имеющих максимальный вес.
всех дуг, имеющих максимальный вес. - Добавляем в
 одну дугу из
одну дугу из 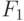 , выбранную произвольно.
, выбранную произвольно. - Из графа
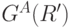 удаляем дуги, входящие в множество
удаляем дуги, входящие в множество  . Вновь полученный граф обозначаем также
. Вновь полученный граф обозначаем также 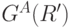 .
. - Из множества
 удаляем пути, содержащие дуги из множества
удаляем пути, содержащие дуги из множества  , построенного на предыдущем этапе. Если
, построенного на предыдущем этапе. Если 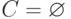 , то построение
, то построение  окончено, иначе переходим к пункту 6.
окончено, иначе переходим к пункту 6. - Произво
Пусть 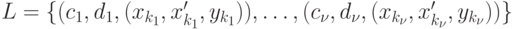 получено по описанному алгоритму, причем дуги в
получено по описанному алгоритму, причем дуги в  занумерованы в том порядке, в котором они присоединялись к
занумерованы в том порядке, в котором они присоединялись к  в соответствии с алгоритмом. Пусть
в соответствии с алгоритмом. Пусть 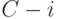 - подмножество всех путей из множества
- подмножество всех путей из множества  , проходящих через дугу
, проходящих через дугу 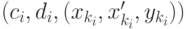 .
.
Лемма 5.1. Для любых 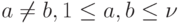 справедливо соотношение
справедливо соотношение 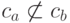 .
.
Доказательство. Для определенности положим, что 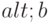 . На основании пункта 4 алгоритма из
. На основании пункта 4 алгоритма из 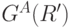 удаляется дуга
удаляется дуга 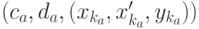 , что влечет за собой удаление из этого же графа и всех путей из множества
, что влечет за собой удаление из этого же графа и всех путей из множества 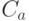 . Это же множество путей удаляется из
. Это же множество путей удаляется из  на основании пункта 5 алгоритма. Присоединение дуги
на основании пункта 5 алгоритма. Присоединение дуги 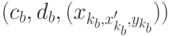 к множеству
к множеству  на основании пункта 2 алгоритма возможно лишь в том случае, если в множестве
на основании пункта 2 алгоритма возможно лишь в том случае, если в множестве  , полученном на предыдущем этапе, есть по крайней мере один путь, проходящий через эту дугу. Поскольку
, полученном на предыдущем этапе, есть по крайней мере один путь, проходящий через эту дугу. Поскольку  после проведенной корректировки заведомо не содержит
после проведенной корректировки заведомо не содержит 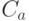 , отсюда следует, что
, отсюда следует, что 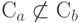 . Обратное соотношение
. Обратное соотношение 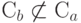 тоже справедливо, так как в противном случае после удаления дуги
тоже справедливо, так как в противном случае после удаления дуги 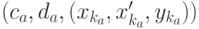 из графа
из графа 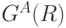 все пути множества
все пути множества 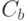 были также удалены, что противоречит предположению о наличии дуги
были также удалены, что противоречит предположению о наличии дуги 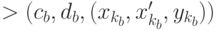 во множестве
во множестве  .
.
В качестве следствия леммы получаем, что для любого 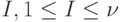 , справедливы соотношения
, справедливы соотношения 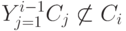 и
и 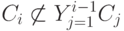 .
.
Отметим следующий очевидный факт: множество выделенных дуг  заведомо принадлежит решению задачи 1 независимо от того, получено ли оно по описанному алгоритму или иным способом.
заведомо принадлежит решению задачи 1 независимо от того, получено ли оно по описанному алгоритму или иным способом.
Из изложенного выше следует, что по предложенному алгоритму строится множество  , не являющееся избыточным в том смысле, что на каждом его шаге из графа
, не являющееся избыточным в том смысле, что на каждом его шаге из графа 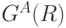 удаляется непустое множество путей, принадлежащих
удаляется непустое множество путей, принадлежащих  . Если
. Если  , то мощность
, то мощность  минимальна и
минимальна и  строится за один шаг.
строится за один шаг.
Рассмотренная нами задача построения множества  дуг эквивалентна задаче о покрытии, или задаче построения минимальной формы булевой функции. Если проводить аналогию с последней задачей, то построенное с помощью предложенного алгоритма множество
дуг эквивалентна задаче о покрытии, или задаче построения минимальной формы булевой функции. Если проводить аналогию с последней задачей, то построенное с помощью предложенного алгоритма множество  соответствует в силу леммы 5.1 приведенной системе простых импликант. Таким образом, вопрос о близости минимального по мощности решения задачи 1 и решения, построенного с помощью предложенного алгоритма, эквивалентен вопросу о близости приведенной системы простых импликант к минимальной приведенной системе импликант (минимальной форме булевой функции). Продолжая аналогию, заметим, что из построенного по предложенному алгоритму множества
соответствует в силу леммы 5.1 приведенной системе простых импликант. Таким образом, вопрос о близости минимального по мощности решения задачи 1 и решения, построенного с помощью предложенного алгоритма, эквивалентен вопросу о близости приведенной системы простых импликант к минимальной приведенной системе импликант (минимальной форме булевой функции). Продолжая аналогию, заметим, что из построенного по предложенному алгоритму множества  некоторые дуги можно удалять способом, подобным способу удаления импликант из приведенной системы [21].
некоторые дуги можно удалять способом, подобным способу удаления импликант из приведенной системы [21].
Проиллюстрируем предложенный способ преобразования автомата в  -БПИ-автомат на примере.
-БПИ-автомат на примере.
Рассмотрим автомат  , заданный табл. 5.1. Пусть
, заданный табл. 5.1. Пусть  .
.
| s\x | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 1 | 2, a | 3, a | 2, a | 1, c |
| 2 | 4, a | 1, b | 2, c | 3, c |
| 3 | 2, b | 4, a | 3, d | 2, f |
| 4 | 3, a | 2, b | 4, f | 3, d |
Вследствие замечания к теореме 5.1 в рассматриваемом примере нам достаточно ограничиться при замене итерации по изложенному выше способу значением  , равным 8, так как в выражении
, равным 8, так как в выражении  до и после итерации
до и после итерации 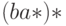 стоит символ
стоит символ  и с учетом этого длина слов в
и с учетом этого длина слов в 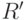 будет доведена до 10 (значение
будет доведена до 10 (значение 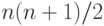 при
при  ) и при этом значении
) и при этом значении  . В результате преобразования
. В результате преобразования  получим следующее выражение:
получим следующее выражение:
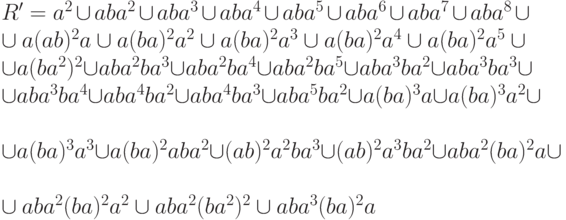
Граф 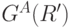 , или, что то же самое,
, или, что то же самое, 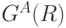 , имеет вид, изображенный на рис. 5.2, где двойные стрелки соответствуют выделенным дугам.
, имеет вид, изображенный на рис. 5.2, где двойные стрелки соответствуют выделенным дугам.
Множество путей  в нашем случае таково:
в нашем случае таково:
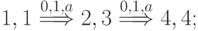
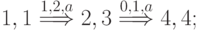
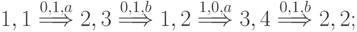
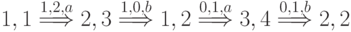
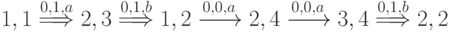
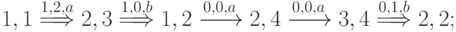
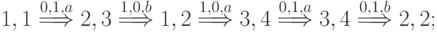
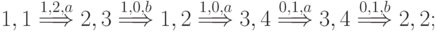
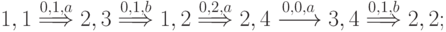
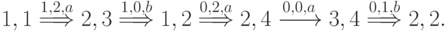
В соответствии с предложенным выше алгоритмом выбора  на первом шаге получаем
на первом шаге получаем 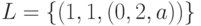 .
.
Далее, максимальный вес, равный 8, в множестве  имеют дуги
имеют дуги 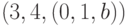 и
и 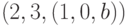 ; тогда полагаем
; тогда полагаем 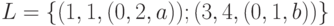 , выбрав первую из названных дуг. После корректировки в множестве
, выбрав первую из названных дуг. После корректировки в множестве  остается два первых пути из списка, приведенного выше. Поскольку вес дуги
остается два первых пути из списка, приведенного выше. Поскольку вес дуги 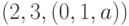 максимален (он равен 2), то добавляем ее в
максимален (он равен 2), то добавляем ее в  и на этом процесс построения
и на этом процесс построения  заканчивается, так как множество
заканчивается, так как множество  после повторной корректировки пустое. Таким образом,
после повторной корректировки пустое. Таким образом, 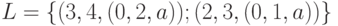
Используя алгоритм 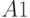 из [23], получаем следующее разбиение множества
из [23], получаем следующее разбиение множества 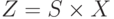 :
:
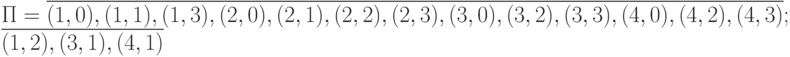
Это разбиение имеет два класса, следовательно, для кодирования символов классов достаточно, например, одной двоичной переменной. Пусть  и
и 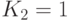 , тогда автомат с контрольными точками будет представлен в табл. 5.2.
, тогда автомат с контрольными точками будет представлен в табл. 5.2.
| s\x | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 1 | 2, a 0 | 3, a 0 | 2, a 1 | 1, c 0 |
| 2 | 4, a 0 | 1, b 0 | 2, c 0 | 3, c 0 |
| 3 | 2, b 0 | 4, a 1 | 3, d 0 | 2, f 0 |
| 4 | 3, a 0 | 2, b 1 | 4, f 0 | 3, d 0 |
Отметим, что идея изложенного метода преобразования автоматов очевидным образом может быть использована и для решения следующей задачи: для заданного регулярного множества  непустых входных слов вывести выходные контрольные точки в автомате таким образом, чтобы каждое слово из
непустых входных слов вывести выходные контрольные точки в автомате таким образом, чтобы каждое слово из  стало диагностическим для автомата с контрольными точками.
стало диагностическим для автомата с контрольными точками.
Предложенный метод решения задачи 1 в качестве одного из этапов содержит построение путей множества  , выполняемого визуально по проверочному графу. Такое построение становится тем более затруднительным, чем большее число состояний имеет данный автомат. В связи с этим рассмотрим формализованный метод построения такого множества
, выполняемого визуально по проверочному графу. Такое построение становится тем более затруднительным, чем большее число состояний имеет данный автомат. В связи с этим рассмотрим формализованный метод построения такого множества  дуг автомата
дуг автомата  , что удаление их превращает автомат
, что удаление их превращает автомат  в
в  -БПИ-автомат. В основу метода положим представление автомата в виде матрицы переходов и выполнение операций над этой матрицей, описанных, например, в работе [18].
-БПИ-автомат. В основу метода положим представление автомата в виде матрицы переходов и выполнение операций над этой матрицей, описанных, например, в работе [18].
Напомним, что для автомата  , имеющего
, имеющего  состояний, матрица переходов состоит из
состояний, матрица переходов состоит из  строк и
строк и  столбцов и обозначается
столбцов и обозначается ![[A]](/sites/default/files/tex_cache/7e2bf8880d46cb84f91d8740b2659a88.png) . Пусть
. Пусть 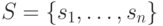 - множество состояний автомата
- множество состояний автомата  и пусть
и пусть  обозначает дугу графа автомата
обозначает дугу графа автомата  , направленную от
, направленную от  к
к 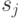 под воздействием входного сигнала
под воздействием входного сигнала  с выдачей выходного сигнала
с выдачей выходного сигнала  . Элемент
. Элемент  матрицы
матрицы ![[A]](/sites/default/files/tex_cache/7e2bf8880d46cb84f91d8740b2659a88.png) , т. е. содержимое клетки, расположенной на пересечении
, т. е. содержимое клетки, расположенной на пересечении  -й строки и
-й строки и  -го столбца, содержит все дуги, ведущие из вершины
-го столбца, содержит все дуги, ведущие из вершины  в вершину
в вершину 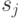 . Если такие дуги отсутствуют, то элемент
. Если такие дуги отсутствуют, то элемент  полагается равным нулю.
полагается равным нулю.
Условимся считать, что обозначение  -го состояния
-го состояния 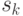 приписано
приписано  -й строке и
-й строке и  -му столбцу матрицы переходов.
-му столбцу матрицы переходов.
В работе [18] введена операция возведения в степень матрицы переходов ![[A]](/sites/default/files/tex_cache/7e2bf8880d46cb84f91d8740b2659a88.png) и доказано, что элемент
и доказано, что элемент  матрицы
матрицы ![[A]^k, k=1,2,\dots](/sites/default/files/tex_cache/2e8df4348dc41ad5ae2510b798e97810.png) , является множеством всех путей длины
, является множеством всех путей длины  , ведущих из состояния
, ведущих из состояния  в состояние
в состояние 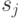 автомата
автомата  . Этот факт и является основой для формализованного нахождения тех путей в графе автомата
. Этот факт и является основой для формализованного нахождения тех путей в графе автомата  , которые являются причиной потери информации.
, которые являются причиной потери информации.

