Инспектор
Вы можете этот курс.
Опубликован: 06.08.2007 | Уровень: профессионал | Доступ: платный
Дополнительный материал 3:
Задачи по разделам курса
Предсказывающий разбор сверху- вниз
4.4.1. Построить множества FIRST и FOLLOW для каждого нетерминала грамматики
![а) S \to aAB|B \ \ \ б) S \to aAB|BA
\\
A \to aA|a \ \ \ A \to BBB|a
\\
B \to BS|A|b; \ \ \ B \to AS|b;
\\
\\
в) S \to S + T \ \ \ г) S \to ABC
\\
S \to T \ \ \ A \to BB|\varepsilon
\\
T \to a \ \ \ B \to CC|a
\\
T \to S[S]; \ \ \ C \to AA|b;
\\
\\
д) S \to aB|bA \ \ \ е) S \to Ba|Ab
\\
A \to aS|bAA|a \ \ \ A \to Sa|AAb|a
\\
B \to bS|aBB|b; \ \ \ B \to Sb|BBa|b;
\\
\\
ж) S \to (SbS) \ \ \ з) B \to begin D; S end
\\
S \to (T) \ \ \ B \to s
\\
S \to a \ \ \ D \to D; d
\\
T \to TS \ \ \ D \to d
\\
T \to S; \ \ \ S \to S; B
\\
S \to B;
\\
\\
и) A \to aACd|b
\\
C \to c|\varepsilon .](/sites/default/files/tex_cache/d322d5ae7a93bd2e9df01f521c02890e.png)
4.4.2. Является ли следующая грамматика LL(1)? Использовать критерий LL(1).
S -> aAb; A -> 0; A -> aaA.
4.4.3. Для грамматики написать эквивалентную LL(1) - грамматику
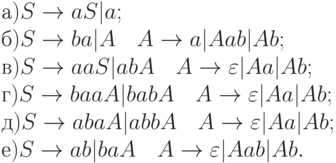
4.4.4. Для следующих грамматик определить, являются ли они LL(k) грамматиками и найти точное значение k. Для LL(1) -грамматик построить детерминированный левый анализатор:
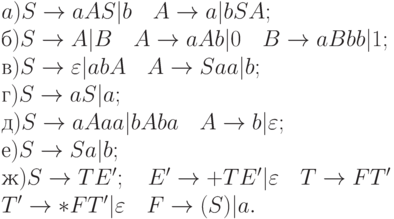
4.4.5. Определить, являются ли следующие грамматики LL(k) -грамматиками, и указать точное значение k:
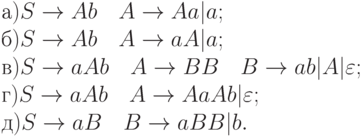
4.4.6. Преобразовать грамматику к LL(1)- виду и построить для неe LL(1) -таблицу
а) S -> Ab A -> aA|a; б) S -> aB B -> aBB|b:
4.4.7. Сколько тактов сделает LL(1) -анализатор для грамматики G c правилами:
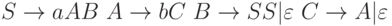
при разборе цепочки x = ab; ab, b?
4.4.8. Является ли грамматика S -> Sa|b LL(2) - грамматикой?
4.4.9. Является ли язык, состоящий из всех целых чисел без знака и без незначащих нулей, LL(1) -языком?
4.4.10. Является ли язык, состоящий из всех цепочек из 0 и 1, не содержащих подцепочки 010, LL(1) -языком?
4.4.11. Является ли язык, состоящий из всех непустых цепочек из 0 и 1, не содержащих трех 1 подряд, LL(1) -языком?
4.4.12. Существует ли контекстно-свободная грамматика, LL(1) -таблица для которой не содержит элементов "ошибка" ?
4.4.13. Сформулируйте необходимые и достаточные условия того, что КС-грамматика есть LL(1) -грамматика. Докажите необходимость и достаточность.
