НОУ ИНТУИТ | Теория и реализация языков программирования. Лекция 3: Задачи по разделам курса

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 06.08.2007 | Уровень: профессионал | Доступ: платный

|

Вам нравится? Нравится 18 студентам

| Поделиться |

Поддержать программу

2.3.19. Построить КС-грамматики для следующих языков:

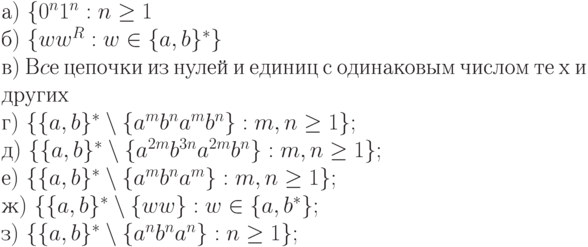
$а)\ \{ 0^{n}1^{n} : n \ge 1 \\ б)\ \{ ww^{R} : w \in \{ a, b\} ^{*}\} \\ в)\ Вcе\ цепочки\ из\ нулей\ и\ единиц\ с\ одинаковым\ числом\ те\ х\ и \\ других \\ г)\ \{ \{ a, b\} ^{*} \setminus \{ a^{m}b^{n}a^{m}b^{n}\} : m, n \ge 1\} ; \\ д)\ \{ \{ a, b\} ^{*} \setminus \{ a^{2m}b^{3n}a^{2m}b^{n}\} : m, n \ge 1\} ; \\ е)\ \{ \{ a, b\} ^{*} \setminus \{ a^{m}b^{n}a^{m}\} : m, n \ge 1\} ; \\ ж)\ \{ \{ a, b\} ^{*} \setminus \{ ww\} : w \in \{ a, b^{*}\} ; \\ з)\ \{ \{ a, b\} ^{*} \setminus \{ a^{n}b^{n}a^{n}\} : n \ge 1\} ;$

2.3.20. Определить КС-грамматики, которые порождали бы следующие языки:

1) все строки - элементы множества {0, 1}* такие, что в каждой из них непосредственно справа от каждого символа 0 стоит символ 1.

2) все строки - элементы множества {0, 1}* такие, что результаты чтения этих строк слева направо и справа налево совпадают;

3) все строки - элементы множества {0, 1}*, которые содержат символов 0 вдвое больше, чем символов 1 ;

4) все строки - элементы множества {0, 1}*, которые имеют одинаковое число символов 0 и 1 ;

5) все строки - элементы множества {0, 1}*, которые имеют четное число символов 0 и нечетное число символов 1 ;

6) все строки - элементы множества {0, 1}*, в которых скобки расставлены правильно.

2.3.21. Построить КС-грамматики, порождающие языки:

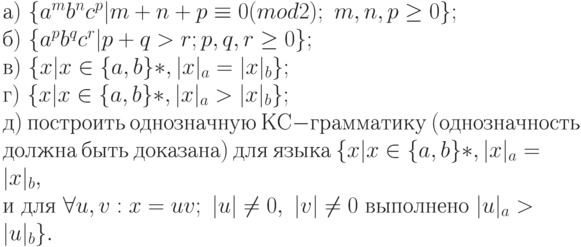
$а)\ \{ a^{m}b^{n}c^{p}|m + n + p \equiv 0(mod 2);\ m, n, p \ge 0\} ; \\ б)\ \{ a^{p}b^{q}c^{r}|p + q > r; p, q, r \ge 0\} ; \\ в)\ \{ x|x \in \{ a, b\} *, |x|_{a} = |x|_{b}\} ; \\ г)\ \{ x|x \in \{ a, b\} *, |x|_{a} > |x|_{b}\} ; \\ д)\ построить\ однозначную\ КС-грамматику\ (однозначность \\ должна\ быть\ доказана)\ для\ языка\ \{ x|x \in \{ a, b\} *, |x|_{a} = |x|_{b}, \\ и\ для\ \forall u, v : x = uv;\ |u| \ne 0,\ |v| \ne 0\ выполнено\ |u|_{a} > |u|_{b}\} .$

2.3.22. Построить КС-грамматику, порождающую язык

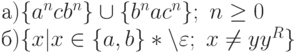
$а) \{ a^{n}cb^{n}\} \cup \{ b^{n}ac^{n}\} ;\ n \ge 0 \\ б) \{ x|x \in \{ a, b\} * \setminus \varepsilon ;\ x \ne yy^{R}\}$

2.3.23. Построить НС-грамматики для следующих языков:

а) 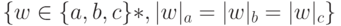$\{ w \in \{ a, b, c\} *, |w|_{a} = |w|_{b} = |w|_{c}\}$ (Винегрет)

б) $\{ w \in \{ a, b, c\} *,\ 3|w|_{a} = 5|w|_{b} = 7|w|_{c}\}$ (Винегрет 2)

в) {aⁿpⁿrⁿ} : n >=; 1} (Три мушкетeра)

г) {a^mbⁿa^mbⁿ : m, n >= 1} (Две калоши)

д) {a^2mbⁿa^mb⁵ⁿ : m, n >= 1} (Калоши 2)

е) {a^mbⁿc^k : m >= n >= k >= 1} (Горка)

ж) {a^mbⁿc^k : 2m >= 3n >= k >= 1} (Горка 2)

з) 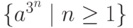$\{a^{3^n}\mid n \geq 1 \}$ (Бог любит троицу)

и) 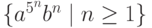$\{a^{5^n}b^n \mid n \geq 1 \}$

к) $\{a^{n^2} : n \geq 1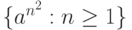\}$ (Квадратные числа)

л) $\{a^{n^2-5n+1} : n \geq 5 \}$

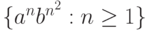м) $\{a^nb^{n^2} : n \geq 1 \}$ (Дама с собачкой)

н) 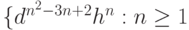$\{d^{n^2-3n+2}h^n : n \geq 1}$

о) {aⁿ : n = 1, 2, 3, 5, 8, 13, ...} (Числа Фиббоначи)

п) {an : n = 1, 3, 6, 10, 15, ...} (Треугольные числа, a_n = n(n + 1)/2 )

р) {aⁿ : n = 1, 5, 12, 22, ...} (Пятиугольные числа, a_n = n + 3n(n - 1)/2. Пятиугольное число может быть разбито на три треугольных + n точек)

с) 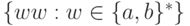$\{ ww : w \in \{ a, b\} ^{*}\}$ (Два лебедя)

т) $\{a^{n^3} : n \geq 1 \}$ (Кубические числа)

у) 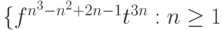$\{f^{n^3-n^2+2n-1}t^{3n} : n \geq 1}$

ф) {aⁿ : n = 1, 2, 6, 24, ... , k!} (Факториал)

х) {01²...0^n-11ⁿ0^n-1...1²0|n >= 1} (Пирамида Хеопса)

ч) {01²...0^n-11ⁿ1ⁿ0^n-1...1²0|n >= 1} (Пирамиды майя)

ш) 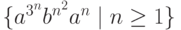$\{a^{3^n}b^{n^2}a^n \mid n \geq 1 \}$

щ) 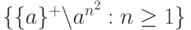$\{ \{ a \} ^+ \backslash a^{n^2} : n \geq 1 \}$ (Для студентов с исследовательской жилкой).

2.3.24. Построить КС-грамматики, порождающие языки

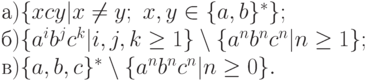
$а) \{ xcy|x \ne y;\ x, y \in \{ a, b\} ^{*}\} ; \\ б) \{ a^{i}b^{j}c^{k}|i, j, k \ge 1\} \setminus \{ a^{n}b^{n}c^{n}|n \ge 1\} ; \\ в) \{ a, b, c\} ^{*} \setminus \{ a^{n}b^{n}c^{n}|n \ge 0\} .$

2.3.25. Пусть G - грамматика с правилами:

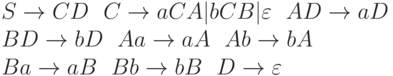
$S \to CD \ \ C \to aCA|bCB|\varepsilon \ \ AD \to aD \\ BD \to bD \ \ Aa \to aA \ \ Ab \to bA \\ Ba \to aB \ \ Bb \to bB \ \ D \to \varepsilon$

Показать, что 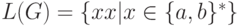$L(G) = \{ xx|x \in \{ a, b\} ^{*}\}$ .

2.3.26. Построить грамматику, порождающую данный язык:

{aⁿcbⁿaⁿcbⁿ|n > 0}:

2.3.27. Построить регулярную грамматику, порождающую цепочки в алфавите (a, b), в котором символ a не встречается два раза подряд.

2.3.28. Построить грамматику, порождающую сбалансированные относительно круглых скобок цепочки в алфавите 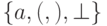$\{a, (, ), \bot \}$ . Сбалансированную цепочку $\alpha$ определим реккурентно: цепочка $\alpha$ сбалансирована, если:

а) $\alpha$ не содержит скобок,

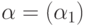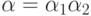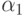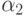б) $\alpha = (\alpha _{1})$ или $\alpha = \alpha _{1}\alpha _{2}$ , где $\alpha _{1 }$ и $\alpha _{2}$ сбалансированы.

2.3.29 Показать, что наличие в КС-грамматике правил вида

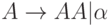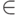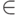а) $A \to AA|\alpha$ б) $A \to A\alpha A|\beta в) A \to \alpha A|A\beta |\gamma$ , где $\alpha$ , $\beta$ , $\gamma$ $\in$ (V_N $\cup$ V_T)^*; A $\in$ V_N, делает еe неоднозначной. Можно ли преобразовать эти правила таким образом, чтобы полученная эквивалентная грамматика была однозначной?

2.3.30. Показать, что грамматика G неоднозначна.

G : S -> abC|aB B -> bc; bC -> bc

2.3.31. Дана КС-грамматика G = (VT, VN, P, S). Предложить алгоритм построения множества

$X = \{ A \in V_{N}|A \varepsilon \} .$

2.3.32. Для произвольной КС-грамматики G предложить алгоритм, определяющий, пуст ли язык L(G).

2.3.33. Одинаковые ли языки порождают грамматики из а), б), в)?

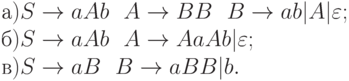
$а) S \to aAb \ \ A \to BB \ \ B \to ab|A|\varepsilon ; \\ б) S \to aAb \ \ A \to AaAb|\varepsilon ; \\ в) S \to aB \ \ B \to aBB|b.$

2.3.34. Эквивалентны ли грамматики с правилами

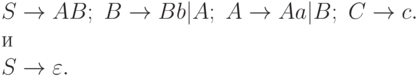
$S \to AB;\ B \to Bb|A;\ A \to Aa|B;\ C \to c. \\ и \\ S \to \varepsilon .$

2.3.35. Эквивалентны ли грамматики с правилами

A -> AB; B -> bC; A -> aAc|Sa; C -> c|Ca.
и
S -> As|Bc; B -> Ac|cS; A -> Bd; C -> c.

Дальше >>

Теория и реализация языков программирования

Теория и реализация языков программирования

Задачи по разделам курса

Вопросы и ответы

Студенты

Авторизоваться

Теория и реализация языков программирования

Теория и реализация языков программирования

Задачи по разделам курса

Вопросы и ответы

Студенты