Атрибутные грамматики

Простые многовизитные атрибутные грамматики

Атрибутная грамматика называется простой k -визитной, если для каждого нетерминала существует разбиение A1(X), ... , Am(X) множества атрибутов A(X), где и m может зависеть от X, то есть m = m(X), такое, что для любого дерева вывода t слова из G существует вычислительная последовательность, при которой для любого вхождения X в t все атрибуты Aj(X) вычисляются при выполнении j -го визита в поддерево c корнем X для всех [7].

Атрибутная грамматика называется простой многовизитной ( SMV ), если она является простой k -визитной для какого-нибудь k.

Существуют абсолютно незацикленные атрибутные грамматики, не являющиеся простыми многовизитными.

Пример B.2. Здесь атрибуты a и b символа A левого поддерева вычисляются на первом визите, а x и y - на втором. Для символа A правого поддерева наоборот - атрибуты x и y вычисляются на первом визите, a и b - на втором ( рис. B.2).

Рис. B.2.

Теорема B.10. Всякая простая k -визитная грамматика является абсолютно незацикленной [7].

Теорема B.11. Задача определения того, является ли произвольная атрибутная грамматика простой многовизитной, NP-полна [7]. Мало того, NP-полна даже задача определения простой 2-визитности [7] Если для каждого символа дано разбиение его атрибутов по визитам, то алгоритм вычисления атрибутов дерева принимает следующий вид:.

Алгоритм B.5.Вычисление атрибутов в простой многовизитной грамматике.

procedure визит_в_поддерево(n, i);
begin вычислить наследуемые атрибуты I(Xn);
 визит_в_поддерево (nj1, ij1);
 ...
 визит_в_поддерево (njm, ijm);
 вычислить синтезируемые атрибуты S(Xn)
end;
beginforj := 1tok(Xr)do
 визит_в_поддерево (r, j){r - корень}
end:

Одновизитные атрибутные грамматики

Интересный частный случай простых многовизитных грамматик представляют одновизитные грамматики (IV)[8].

Графом BG братьев правила p будем называть граф, вершинами которого являются символы правой части правила p : X₀->X₁ ... X_np и из Xi в Xj идет дуга тогда и только тогда, когда какие-либо элементы I(Xj) зависят от каких-либо элементов

Теорема B.12. Атрибутная грамматика является одновизитной тогда и только тогда, когда ни один из графов братьев BGp не содержит ориентированных циклов [9].

Из этой теоремы непосредственно следует

Теорема B.13. Задача определения того, является ли произвольная атрибутная грамматика одновизитной, полиномиальна.

Задача планирования визитов для одновизитных грамматик сводится к нахождению какого-нибудь линейного порядка братьев каждого правила, удовлетворяющего частичному порядку, определяемому графом братьев BGp: Алгоритм вычисления атрибутов для одновизитных грамматик выглядит следующим образом:

Алгоритм B.6. Вычисление атрибутов в одновизитной грамматике.

procedure визит_в_поддерево (n);
begin вычислить наследуемые атрибуты I(X);
 в соответствии с линейным порядком символов
 правой части правила
 do визит_в_поддерево (n);
 вычислить синтезируемые атрибуты S(X)
end;
begin визит_в_поддерево(r) {r - корень}
end.

Многопроходные грамматики

Пусть на последовательность визитов наложено такое ограничение, чтобы они образовали последовательные обходы дерева разбора либо сверху-вниз слева-направо, либо сверху- вниз справа-налево.

Атрибутная грамматика называется чистой k - проходной в обоих направлениях, если существует такая последовательность из k обходов <d1 ... dl> (каждое di - либо справа-налево, либо слева-направо), что атрибуты любого дерева вывода могут быть вычислены в результате выполнения этой последовательности обходов [5].

Атрибутная грамматика называется чистой многопроходной в обоих направлениях ( PBD ), если она является чистой k -проходной в обоих направлениях для какого-нибудь k.

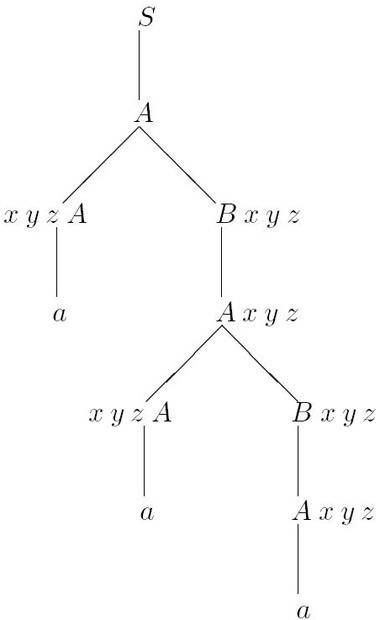
Пример B.3.Существуют атрибутные грамматики, не являющимися чистыми многопроходными ни для какого k ( рис. B.3).

Рис. B.3.

Число необходимых проходов в этом примере зависит от глубины дерева и может быть сколь угодно большим.

Очевидно, что грамматика примера рис. B.1 не является чистой многопроходной и нетрудно видеть, что грамматика примера рис. B.1 является абсолютно незацикленной.

Теорема B.14. Задача определения того, является ли произвольная атрибутная грамматика чистой многопроходной в обоих направлениях, зависит экспоненцально от размера атрибутной грамматики.

Атрибутная грамматика называется чистой k -проходной слева-направо, если атрибуты любого дерева вывода в ней могут быть вычислены за k обходов дерева вывода слева- направо [2, 5].

Атрибутная грамматика называется чистой многопроходной слева-направо ( PLR ), если она является чистой k -проходной слева-направо для какого-нибудь k.