Атрибутные грамматики

Вычислительные последовательности и корректность. Определение визита

Назовем вычислительной последовательностью [4] для дерева вывода t в AG последовательность вида:

c_s = (n₁, A₁)(n₂, A₂)(n₂, A₂) ... (n_r, A_r);

где

1. n_j - внутренняя вершина t (в частности, корень);
2. если n_j#n_j + 1, то n_j + 1 - отец, сын или брат n_j ;
3. A_j - либо подмножество синтезируемых атрибутов n_j, либо подмножество наследуемых атрибутов (то есть либо либо ;
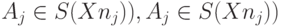4. n₁ = n_r - корень дерева;
5. атрибуты A_j не зависят от A_j для i >= j ;
6. рассмотрим какую-либо внутреннюю вершину n дерева t. Тогда вычислительную последовательность cs можно записать в следующем виде: c_s = u₁(n, B₁)u₂(n, B₂) ... (n, B_h)u_h+1, где подпоследовательности u₁ ... u_h+1 не содержат элементов вида (n, A). Тогда
   1. B_j <= I(X_n), если j нечетно;
   2. B_j <= S(X_n), если j четно,
   3. - вычисляются все атрибуты каждого символа X ;
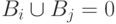   4. , если i#j - все атрибуты вычисляются по одному разу.
   5. пусть c_s = c_s1<n, B_j><n₁, A₁><n₂, A₂>...<n, B_j+1> c_s2, если j нечетно (четно), то n_j - вершины поддерева с корнем n (вершины t вне поддерева с корнем n ).

Таким образом при входе "вниз" в поддерево вычисляются некоторые наследуемые атрибуты корня поддерева, при возврате из поддерева вычисляются некоторые синтезируемые атрибуты корня поддерева.

Назовем незацикленную атрибутную грамматику корректной, если для всякого еe атрибутированного дерева существует вычислительная последовательность.

Теорема B.4. Незацикленная атрибутная грамматика корректна тогда и только тогда, когда для каждого правила p : X₀->X₁ ... X_np если , то имеется в точности одно семантическое правило, сопоставленное p и определяющее значение a(X_i), и если , то имеется в точности одно семантическое правило, сопоставленное p и определяющее значение a(X₀).

Теорема B.5. Сложность проверки незацикленной атрибутной грамматики на корректность линейна по размеру атрибутной грамматики.

Пусть t - дерево вывода и n - его внутренняя вершина. Рассмотрим вычислительную последовательность для t вида c_s = c_s1<n, B₁>c_s2<n, B₂>c_s3, где n входит в c_s1 чeтное число раз, и не входит в c_s2. Последовательность c_s2 обходит поддерево с корнем n. Будем говорить, что <n, B₁>c_s2<n, B₂> определяет визит в поддерево с корнем _n и что вершина n в результате этого визита посещается один раз. Таким образом, если n входит в c_s 2h раз, то n посещается h раз.

Чистые многовизитные грамматики

Будем говорить, что атрибутированное дерево k -визитно, если существует вычислительная последовательность c_s для t такая, что никакая вершина n из t не посещается более k раз.

Атрибутная грамматика называется чистой k -визитной ( PMV ), если каждое атрибутированное дерево вывода t в AG k -визитно [5, 7].

Теорема B.6. Для всякой корректной атрибутной грамматики существует k такое, что грамматика является чистой k -визитной.

На самом деле это k не превосходит максимального по всем символам грамматики числа синтезируемых или наследуемых атрибутов.

Следствием этого являются две следующие теоремы.

Теорема B.7. Сложность задачи определения того, является ли произвольная атрибутная грамматика чистой k -визитной для какого-нибудь k > 0, экспоненциальна.

Эта задача просто совпадает с задачей определения корректности атрибутной грамматики.

Теорема B.8. Сложность задачи определения того, является ли произвольная атрибутная грамматика чистой k -визитной для фиксированного k также экспоненциальна.

Атрибуты всякого дерева t чистой k -визитной атрибутной грамматики можно вычислить с помощью следующего алгоритма:

Алгоритм B.2. Вычисление атрибутов чистой k - визитной атрибутной грамматики

procedure  визит_в_поддерево (n, i);
{n - корень поддерева;
i - номер визита в это поддерево}
{Предполагается, что в вершине n
применено правило вывода p}
begin вычислить некоторые наследуемые атрибуты Xn;
{эти атрибуты определяются <nj1, A> для начала i-го
визита в соответствующей вычислительной
последовательности}
визит_в_поддерево (n, i);
{Xnij - символ правой части правила pg
.
.
.
визит_в_поддерево (njl, ijl);
вычислить некоторые синтезируемые атрибуты Xn
end;
begin for j := 1 to k do визит_в_поддерево(r, j)
  {r - корень дерева}
end end.

В зависимости от того, какие ограничения будут накладываться на порядок посещения вершин и выбор атрибутов, вычисляемых на том или ином визите, будут получаться те или иные классы атрибутных грамматик.