НОУ ИНТУИТ | Защита информации в электронных платежных системах. Лекция 3: Методы защиты информации в компьютерных системах и сетях

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 24.10.2016 | Уровень: для всех | Доступ: платный

|

Вам нравится? Нравится 27 студентам

| Поделиться |

Поддержать программу

3.10. Электронная подпись

3.10.1. Схема классической электронной подписи

Схемы контроля целостности, рассмотренные в разделе 3.8, могут использоваться только при взаимодействии доверяющих друг другу сторон. Они принципиально не способны обеспечивать улаживание возникающих между ними противоречий и разногласий. Такая возможность появляется только при использовании односторонних функций с секретом для формирования электронной или цифровой подписи. Протоколы или схемы электронной подписи являются основным криптографическим средством обеспечения аутентичности информации:

с помощью электронной подписи получатель документа может доказать, что он принадлежит отправителю, при этом автор подписи не сможет оспорить факт отправки подписанного документа;
электронную подпись невозможно подделать, только абонент, чья подпись стоит на документе, мог подписать данный документ;
электронная подпись является неотъемлемой частью документа, перенести ее на другой документ нельзя;
ни противник, ни получатель не могут изменить документ, оставив данный факт незамеченным;
любой пользователь, имеющий образец подписи, может удостовериться в подлинности документа.

Для повышения надежности схемы электронной подписи, например для противодействия атакам перехвата и повтора сообщений, фальсификации времени отправки сообщений, ее можно сделать зависимой от неповторяющегося блока данных nrb.

Схема электронной подписи включает в себя:

параметр безопасности n, в качестве которого может выступать длина подписи, длина подписываемых блоков данных и т.п.;
пространство исходных сообщений;
максимальное число подписей (signature bound), которые могут быть получены в данной схеме без замены секретной информации;
алгоритм G генерации ключей, формирующий по заданному параметру n пару

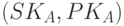(SK_A, PK_A) ,

где		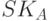-	секретный ключ подписывающего (абонента А),
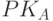		-	соответствующий открытый ключ проверяющего (абонента В);

алгоритм S формирования подписи, вырабатывающий по заданным исходному сообщению M и секретному ключу 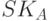подпись sign для сообщения M;
алгоритм V проверки (verification), дающий на выходе при заданных сообщению M, открытому ключу 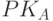и подписи либо значение 1, когда подпись сообщения принимается, либо 0, когда подпись отвергается.

Подпись 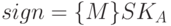$sign = \{M\}SK_A$ называется допустимой для сообщения M, если она принимается алгоритмом V с вероятностью, близкой к 1. Подделкой подписи сообщения M называется нахождение противником, не имеющим секретного ключа подписывающего, допустимой подписи для этого сообщения.

В общем случае неинтерактивный протокол электронной подписи имеет следующий вид.

Схема электронной подписи документа M.

Отправитель А вычисляет

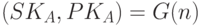
и посылает 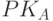получателю В, сохраняя 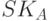в секрете.
Для получения подписи документа M отправитель А вычисляет

и посылает M и sign получателю В.
Получатель В вычисляет

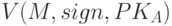
и в зависимости от результата принимает или отвергает подпись sign сообщения M.

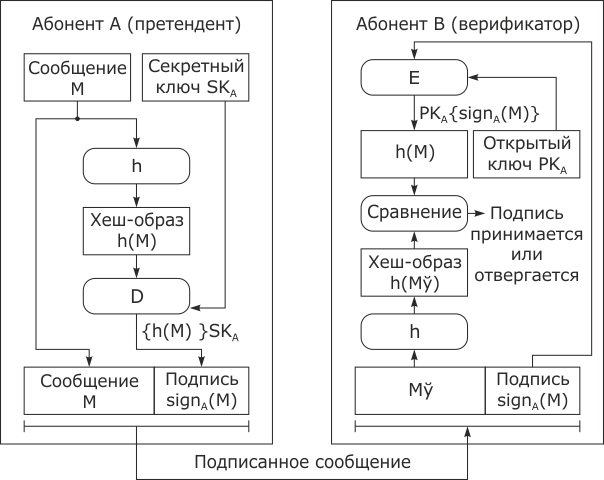
В классической схеме электронной подписи, приведенной на рис. 3.34, предполагается, что подписывающий (абонент А) знает содержание документа M, который он подписывает; проверяющий (абонент В), зная открытый ключ проверки подписи, может проверить правильность подписи в любое время без какого-либо разрешения или участия претендента А.

Рис. 3.34. Классическая схема создания и проверки электронной подписи

При создании электронной подписи по классической схеме претендент А выполняет следующую последовательность действий:

применяет к исходному сообщению M хеш-функцию h и формирует хеш-образ сообщения h (M) (при необходимости дополняя входную информационную последовательность до требуемой длины);
при необходимости дополняет хеш-образ до требуемой длины, формируя h* (M) = ext h (M);
вычисляет электронную подпись sign с использованием несимметричного криптоалгоритма D и секретного ключа создания подписи :
$sign = \{h* (M)\} SK_A$ .

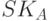Хеш-функция является неотъемлемой частью схем электронной подписи. Применение медленных несимметричных криптоалгоритмов для преобразования всего исходного сообщения M нерационально, поэтому для повышения быстродействия схемы перед процедурой формирования подписи используется функция необратимого сжатия информации.

Последовательность действий абонента В, получившего подписанное сообщение:

верификатор В применяет к тексту полученного сообщения хеш-функцию; дополняет в случае необходимости хеш-образ сообщения до требуемой длины (на рис. 3.34 рассматривается случай, когда расширение ext h (M) не требуется);
применяет к полученной подписи sign несимметричный криптоалгоритм E с использованием открытого ключа проверки подписи 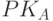и сравнивает полученное значение $PK_A\{sign\}$ с найденным на предыдущем шаге h* (M), при положительном результате сравнения подпись признается, в противном случае отвергается.

3.10.2. Хеш-функции

Хеш-функцией называется преобразование h (х), превращающее информационную последовательность M произвольной длины в информационную последовательность (хеш-образ) фиксированной длины h (M).

К функции h (х) предъявляются четыре основных требования:

результат работы хеш-функции должен зависеть от всех двоичных символов исходного сообщения, а также от их взаимного расположения, т.е. h (х) должна быть чувствительна к любым изменениям входной информационной последовательности;
хеш-функция должна быть стойкой в смысле обращения;
хеш-функция должна быть стойкой в смысле нахождения коллизий;
хеш-функция должна быть стойкой в смысле нахождения второго прообраза.

Второе, третье и четвертое требования означают, что задачи нахождения последовательности M по заданному хеш-образу h (M), нахождения двух различных сообщений, имеющих одинаковые хеш-образы, и нахождения для заданной последовательности M другой последовательности M`, M` 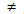M, такой что h (M`) = h (M), должны быть вычислительно неразрешимы.

Области использования хеш-функций:

защита паролей при их передаче и хранении;
формирование контрольных кодов MDC и НМАС;
получение сжатого образа сообщения перед формированием электронной подписи;
необратимое преобразование случайного запроса при аутентификации по принципу запрос-ответ;
оперативный контроль хода программ (concurrent checking of program flow).

Наиболее известные алгоритмы получения хеш-образов сообщений - MD5, SHA, TIGER.

MD5 — представитель семейства алгоритмов вычисления хеш-функций MD (Message Digest Algorithm), предложенного Р. Ривестом; разработан в 1991 г.; преобразует информационную последовательность произвольной длины в хеш-образ разрядностью 128 бит. Самый быстродействующий алгоритм хеширования.

TIGER - разработан Р. Андерсоном и Э. Бихэмом; предназначен для реализации на 64-разрядных компьютерах; преобразует информационную последовательность произвольной длины в хеш-образ разрядностью 192 бита.

3.10.3. Secure Hash Algorithm (SHA)

Алгоритм SHA является частью стандарта SHS (Secure Hash Standard), принятого в 1993 г. Национальным институтом стандартов и технологий США (NIST) и Агентством национальной безопасности США. SHA использует принципы, предложенные ранее Р. Ривестом при разработке своих алгоритмов MD4 и MD5.

Рассмотрим версию SHA-1, в которой осуществляется преобразование информационной последовательности произвольной длины в хеш-образ разрядностью 160 бит.

На первом этапе информационная последовательность дополняется до длины, кратной 512 битам. Сначала информационная последовательность дополняется до длины на 64 двоичных разряда меньшей числа, кратного 512: к концу последовательности (сообщения) приписывается 1, а затем необходимое количество нулей. После этого приписывается 64-разрядный код длины сообщения. Если длина исходного сообщения больше 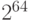$2^{64}$ , используются только 64 младших разряда этого кода.

Пусть после дополнения получена информационная последовательность

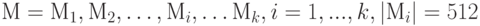$М = М_1, М_2, \ldots, М_i, \ldots М_k, i= 1, ..., k, |М_i| = 512$ .

На вход i-го основного цикла SHA_i преобразования поступает i-й блок информационной последовательности и результат работы предыдущего цикла $SHA_{i – 1}$ , т.е.:

$SHA_i = h (М_i, SHA_{i – 1})$ .

Перед началом каждого цикла соответствующий блок расширяется до 80 слов по 32 разряда в каждом. Расширение происходит следующим образом. Допустим,

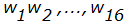— исходный блок,

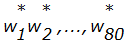— расширенный блок, при этом

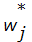
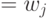= w_j для j = 1, ..., 16,

для j = 17, ..., 80,

где

Rol

-

операция циклического сдвига на один разряд влево.

Перед началом первого цикла инициализируются пять 32-разрядных переменных

A = 67452301h; B = EFCDAB89h; C = 98BADCFEh;

D = 10325476h; E = C3D2E1F0h,

при этом стартовый вектор хеширования (синхропосылка) есть результат конкатенации этих переменных, т.е.:

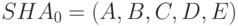SHA_0 = (A, B, C, D, E) .

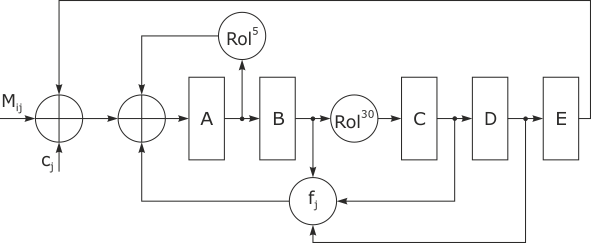
Конкатенация новых значений этих переменных, полученных в конце i-го цикла, объявляется результатом работы цикла SHA_i . Схема одного шага алгоритма хеширования приведена на рис. 3.35.

Рис. 3.35. Схема одного шага алгоритма SHA

В начале каждого цикла создаются копии входных переменных:

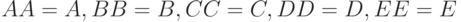AA = A, BB = B, CC = C, DD = D, EE = E .

Затем выполняется 80 шагов алгоритма, на каждом из которых происходит выполнение следующих операций:

$Temp = Rol^5A + f_i (B, C, D) + E + M_{ij} + cj$ ,

E = D ,

D = C ,

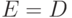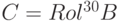$C = Rol^{30}B$ ,

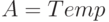A = Temp ,

где		-	операция циклического сдвига на n разрядов влево;
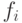		-	шаговая функция;
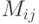	$M_{ij}$	-	j-е слово i-го блока ;
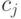		-	шаговая константа;
	j	=	1, ..., 80;
	i	=	1, ..., k.

В первом раунде (при j = 1, ..., 20) используются функция

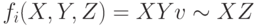$f_i (X, Y, Z) = XY v \sim XZ$ ,

где

$\sim$

-

операция отрицания,

и константа

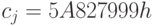c_j= 5A827999h ;

во втором раунде (при j = 21, ..., 40) используются функция

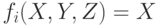
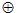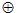f_i (X, Y, Z) = X Y Z

и константа

c_j = 6ED9EBA1h ;

в третьем раунде (при j = 41, ..., 60) используются функция

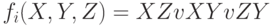
f_i (X, Y, Z) = XZ v XY v ZY

и константа

c_j= 8F1BBCDCh ;

в четвертом раунде (при j = 61, ..., 80) используются функция

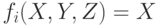
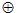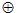f_i (X, Y, Z) = X Y Z

и константа

c_j = CA62C1D6h ;

Цикл завершается сложением по модулю $2^{32}$ полученных значений A, B, C, D и E соответственно с AA, BB, CC, DD и EE:

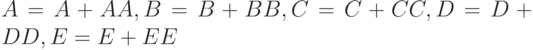A = A + AA, B = B + BB, C = C + CC, D = D + DD, E = E + EE ;

конкатенация полученных значений A, B, C, D и E является результатом работы основного цикла.

В настоящее время существуют версии алгоритма SHA-256, SHA-384, SHA-512.

3.10.4. Протокол электронной подписи RSA

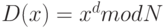Допустим, E (x) = x^e mod N - открытая функция зашифрования, а D (x) = x^d mod N - секретная функция расшифрования, где 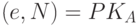(e, N) = PK_A - открытый ключ абонента А, 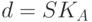d = SK_A - секретный ключ абонента А.

Схема электронной подписи RSA.

Абонент А (претендент) вычисляет хеш-образ h (M) сообщения M.
Абонент А зашифровывает полученное значение h (M) на своем секретном ключе 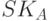, вычисляя подпись
$sign_A (M) = \{M\} SK_A = h (M)^d mod N$ ,

и отправляет абоненту В пару документ-подпись .
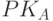Абонент В (верификатор) расшифровывает на открытом ключе отправителя, т.е. вычисляет
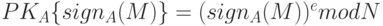$PK_A\{sign_A (M)\} = (sign_A (M))^e mod N$ .
Абонент В вычисляет хеш-образ h (M) полученного сообщения и проверяет равенство
.

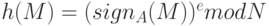В случае положительного результата проверки подпись принимается, в противном случае - отвергается.

3.10.5. Классификация атак на схемы электронной подписи

Стойкость схемы электронной подписи зависит от стойкости используемых криптоалгоритмов и хеш-функций и определяется относительно пары угроза-атака.

Приведем классификацию атак на схемы электронной подписи:

атака на основе известного открытого ключа (key-only attack) - самая слабая из атак, практически всегда доступная противнику;
атака на основе известных подписанных сообщений (known-message attack) - в распоряжении противника имеется некоторое число пар (M, sign (M)), где M - некоторое сообщение, а sign (M) - допустимая подпись для него, при этом противник не может влиять на выбор M;
простая атака с выбором подписанных сообщений (generic chosen-message attack) - противник имеет возможность выбрать некоторое количество подписанных сообщений, при этом открытый ключ он получает после этого выбора;
направленная атака с выбором сообщений (directed chosen-message attack) - выбирая подписанные сообщения, противник знает открытый ключ;
адаптивная атака с выбором сообщений (adaptive chosen-message attack) - противник знает открытый ключ, выбор каждого следующего подписанного сообщения он может делать на основе знания допустимой подписи предыдущего выбранного сообщения.

Каждая атака направлена на достижение определенной цели. Можно выделить следующие виды угроз для схем электронной подписи (в порядке возрастания силы):

экзистенциальная подделка (existential forgery) - создание противником подписи для какого-нибудь, возможно бессмысленного, сообщения M`, отличного от перехваченного;
селективная подделка (selective forgery) - создание подписи для заранее выбранного сообщения;
универсальная подделка (universal forgery) - нахождение эффективного алгоритма формирования подписи, функционально эквивалентного S;
полное раскрытие (total break) - вычисление секретного ключа, возможно отличного от 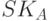, соответствующего открытому ключу 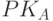, что дает возможность формировать подписи для любых сообщений.

Наиболее стойкими являются схемы, стойкие против самой слабой из угроз на основе самой сильной из атак, т.е. против экзистенциальной подделки на основе атаки с выбором подписанных сообщений. Справедливо следующее утверждение. Схемы электронной подписи, стойкие против экзистенциальной подделки на основе атаки с выбором подписанных сообщений, существуют тогда и только тогда, когда существуют односторонние функции.

3.10.6. Процедура разрешения споров

Для практического применения схем электронной подписи помимо алгоритмов формирования подписи и ее верификации требуется процедура арбитража, т.е. разрешения споров. Арбитраж необходим, когда один из абонентов, например В, предъявляет сообщение и подпись (M, sign_A (M)) , утверждая, что эта пара сообщение-подпись была получена от абонента А, а А отказывается признавать эту подпись своей. С юридической точки зрения основанием для разрешения подобных споров в суде является подписание (обычным образом) каждым пользователем при подключении к системе специального документа, в котором пользователь принимает все "правила игры" вплоть до судебной ответственности. При разборе дела в суде арбитр выступает в качестве эксперта, дающего заключение о подлинности электронной подписи.

Алгоритм арбитража.

Абонент В предъявляет арбитру электронный документ и подпись.
Арбитр требует от абонента А предъявления своего секретного ключа. Если А отказывается, арбитр дает заключение, что подпись подлинная.
Арбитр выбирает из сертифицированного справочника открытый ключ абонента А и проверяет его соответствие секретному ключу, предъявленному А. Если они совпадают, арбитр переходит к шагу 5.
При обнаружении факта несоответствия ключей арбитр обращается в центр сертификации и требует предоставления заверенного абонентом А документа, содержащего его открытый ключ. Если выясняется, что открытый ключ, взятый из справочника, не совпадает с указанным в документе, арбитр признает подпись, предъявленную В, подлинной; при этом все издержки такого решения компенсируются за счет центра. Если открытые ключи в справочнике и документе совпадают, т.е. абонент А предъявил некорректный секретный ключ, арбитр признает подлинность электронной подписи.
Арбитр проверяет соответствие друг другу подписи и документа. При положительном результате проверки подпись признается подлинной, в противном случае отвергается.

Задача арбитража значительно сложнее, чем кажется на первый взгляд. Арбитраж и решение споров в суде невозможны в следующих случаях:

секретный ключ сформирован не самим абонентом А, а специальным центром генерации ключей;
аппаратура, на которой выполняется алгоритм генерации или проверки подписи, содержит какие-либо элементы, не контролируемые пользователем ("черные ящики", защищенные участки памяти и т.п.).

Наконец, возможны безвыходные ситуации, в которых арбитр не может принять никакого обоснованного решения. Например, абонент В предъявляет sign_A (M) и утверждает, что это подпись под документом M. Абонент А признает, что это его подпись, но под документом M`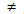M, при этом выясняется, что хеш-образы этих документов совпадают, т.е. h (M`) = h (M) . Арбитр понимает, что кто-то из двоих нашел коллизию для применяемой в схеме электронной подписи хеш-функции, и оказывается в патовой ситуации. Выход из положения возможен только в том случае, если заранее обговорен порядок разрешения спора в такой ситуации.

3.10.7. Особые схемы электронной подписи

В некоторых ситуациях могут потребоваться схемы электронной подписи, отличные от рассмотренной классической схемы. Известны следующие специальные схемы электронной подписи:

схема слепой подписи, когда абонент А подписывает документ, не зная его содержимого;
схема групповой подписи, которая позволяет верификатору убедиться в принадлежности полученного сообщения некоторой группе претендентов, но кто именно из членов группы подписал документ, верификатор определить не в состоянии;
схема разделяемой подписи, которая формируется только при участии определенного количества участников протокола, иначе говоря, данная схема является объединением классической схемы подписи и схемы разделения секрета;
схема конфиденциальной (неотвергаемой) подписи, которая не может быть проверена без участия сформировавшего ее участника протокола;
схема неоспоримой подписи, в которой подделка подписи может быть доказана.

Дальше >>

Защита информации в электронных платежных системах

Защита информации в электронных платежных системах