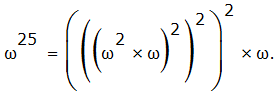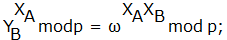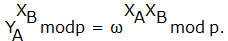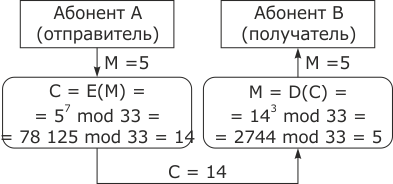| Россия, г. Туймазы |
Методы защиты информации в компьютерных системах и сетях
3.6. Криптосистемы с открытым ключом
Основной проблемой, возникающей при использовании криптосистем с секретным ключом, рассмотренных в разделе 3.5, является проблема распределения ключей. Учитывая что процедуры зашифрования и расшифрования выполняются с помощью одного и того же ключа, в системе с n абонентами потребуется n (n – 1) : 2 ключей, которые не только должны быть сгенерированы, но и надежным образом распределены среди всех участников информационного обмена. Необходимость наличия недоступных для противника секретных каналов для обмена ключами делает такой подход к построению системы секретной связи чрезвычайно дорогостоящим мероприятием, практически не применимым в коммерческих сетях связи, в региональных и глобальных информационных системах и естественно абсолютно недоступным частным лицам. Еще в 40-х гг. ХХ в. К. Шеннон предложил строить шифр таким образом, чтобы задача его вскрытия была эквивалентна решению некоей математической задачи, требующей объема вычислений, недоступного для современных компьютеров. Реализация этой идеи стала возможной, когда в 70-х гг. Диффи и Хеллман предложили принципиально новый способ организации секретной связи без предварительного обмена ключами, так называемое шифрование с открытым ключом. При этом для зашифрования и расшифрования используются разные ключи, и знание одного из них не дает практической возможности определить второй. В результате ключ зашифрования может быть сделан открытым без потери стойкости шифра, и лишь ключ расшифрования держится получателем в секрете.
3.6.1. Односторонние функции
Базовым понятием нового направления в криптографии является понятие односторонней функции (one-way function). По заданному аргументу 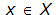 вычислить значение этой функции F(x) можно, в то же время определение x из F(x) задача вычислительно неразрешимая. Теоретически x по известному значению F(x) можно найти всегда, проверяя по очереди все возможные значения x до тех пор, пока соответствующее значение F(x) не совпадет с заданным. Однако практически при значительной размерности множества X такой подход неосуществим.
вычислить значение этой функции F(x) можно, в то же время определение x из F(x) задача вычислительно неразрешимая. Теоретически x по известному значению F(x) можно найти всегда, проверяя по очереди все возможные значения x до тех пор, пока соответствующее значение F(x) не совпадет с заданным. Однако практически при значительной размерности множества X такой подход неосуществим.
Итак, односторонней функцией называется функция 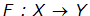 , обладающая двумя свойствами:
, обладающая двумя свойствами:
- задача нахождения значений F (x) вычислительно разрешима;
- задача инвертирования F (x) вычислительно неразрешима.
До сих пор ни для одной функции, кандидата на звание односторонней, не доказано свойство 2.
Примером кандидата на звание односторонней функции является модульное возведение в степень, т.е. функция 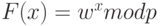 , где p - большое простое число, w - примитивный элемент поля GF (p). То что эта функция может быть эффективно вычислена даже при разрядности параметров в несколько сот знаков, можно показать на примере.
, где p - большое простое число, w - примитивный элемент поля GF (p). То что эта функция может быть эффективно вычислена даже при разрядности параметров в несколько сот знаков, можно показать на примере. 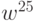 можно вычислить с помощью всего лишь шести операций умножения (умножением считается и возведение в квадрат), так как
можно вычислить с помощью всего лишь шести операций умножения (умножением считается и возведение в квадрат), так как
Далее при вычислении  взятие модуля во избежание получения очень больших чисел следует делать после каждого умножения.
взятие модуля во избежание получения очень больших чисел следует делать после каждого умножения.
Задача вычисления функции, обратной модульному возведению в степень, называется задачей дискретного логарифмирования. На сегодняшний день не известно ни одного эффективного алгоритма вычисления дискретных логарифмов больших чисел.
Односторонняя функция в качестве функции зашифрования неприменима, так как, хотя F (x) - надежно зашифрованное сообщение x, никто, в том числе и законный получатель, не сможет восстановить x. Обойти эту проблему можно с помощью односторонней функции с секретом (one-way trapdoor function).
Такова, например, функция 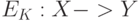 , имеющая обратную
, имеющая обратную 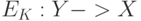 , однако узнать обратную функцию только по
, однако узнать обратную функцию только по  без знания секрета K вычислительно невозможно.
без знания секрета K вычислительно невозможно.
Таким образом, односторонней функцией с секретом K называется функция 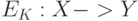 , зависящая от параметра K и обладающая тремя свойствами:
, зависящая от параметра K и обладающая тремя свойствами:
- при любом K задача нахождения значений
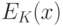 вычислительно разрешима;
вычислительно разрешима; - при неизвестном K задача инвертирования
 вычислительно неразрешима;
вычислительно неразрешима; - при известном K задача инвертирования
 вычислительно разрешима.
вычислительно разрешима.
Функцию  можно использовать для зашифрования информации, а обратную ей функцию
можно использовать для зашифрования информации, а обратную ей функцию  - для расшифрования, так как при всех
- для расшифрования, так как при всех 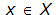 справедливо:
справедливо:
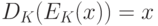 .
.
При этом подразумевается, что тот, кто знает, как зашифровывать информацию, вовсе не обязательно должен знать, как ее расшифровывать. Так же, как и в случае с односторонней функцией, вопрос о существовании односторонних функций с секретом открыт. Для практической криптографии найдено несколько функций, кандидатов на звание односторонней функции с секретом. Для них второе свойство не доказано, однако известно, что задача инвертирования при неизвестном K эквивалентна некоторой хорошо изученной и давно известной трудной математической задаче.
Применение рассмотренных функций для шифрования информации позволяет:
- избавиться от необходимости секретных каналов связи для предварительного обмена ключами;
- свести проблему взлома шифра к решению трудной математической задачи, т.е. в конечном счете принципиально по-другому подойти к обоснованию стойкости криптосистемы;
- решать средствами криптографии задачи, отличные от шифрования, например задачу обеспечения юридической значимости электронных документов.
3.6.2. Модель криптосистемы с открытым ключом
Криптосистему с открытым ключом (public key cryptosystem), основанную на применении односторонних функций с секретом, можно реализовать следующим образом. Пользователь B, который хочет получать конфиденциальные сообщения, должен выбрать одностороннюю функцию 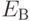 с секретом (ключом)
с секретом (ключом) 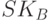 (secret key). Он сообщает всем заинтересованным лицам, например публикует в справочнике открытых ключей, свой открытый ключ
(secret key). Он сообщает всем заинтересованным лицам, например публикует в справочнике открытых ключей, свой открытый ключ 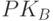 (public key), необходимый для реализации преобразования
(public key), необходимый для реализации преобразования 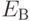 . При этом ключ
. При этом ключ 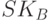 , а следовательно, и алгоритм расшифрования
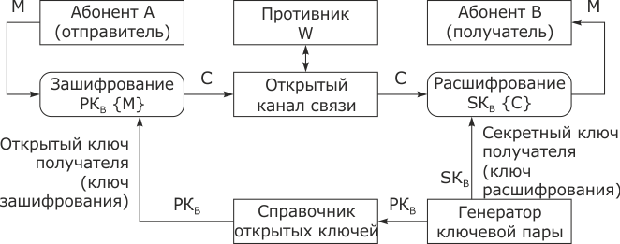
, а следовательно, и алгоритм расшифрования 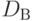 , держатся в секрете. Структура подобной системы приведена на
рис.
3.20.
, держатся в секрете. Структура подобной системы приведена на
рис.
3.20.
Теперь если пользователь A хочет послать B секретное сообщение M, то он находит в справочнике 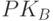 , а затем вычисляет
, а затем вычисляет
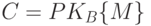
и посылает шифротекст C по открытому каналу пользователю B. Последний, зная секрет 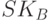 , т.е. умея инвертировать
, т.е. умея инвертировать 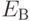 , определяет M по полученному C, вычисляя
, определяет M по полученному C, вычисляя
 .
.
Противник, не зная ключа 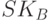 , в силу второго свойства односторонней функции с секретом не сможет прочитать секретную информацию. В отличие от криптосистемы с секретным ключом, если абонент A, зашифровав некоторое сообщение M для абонента B, сохранит шифротекст C, но потеряет M или забудет его содержание, он не будет иметь никаких преимуществ перед противником в раскрытии исходного текста M по известному C.
, в силу второго свойства односторонней функции с секретом не сможет прочитать секретную информацию. В отличие от криптосистемы с секретным ключом, если абонент A, зашифровав некоторое сообщение M для абонента B, сохранит шифротекст C, но потеряет M или забудет его содержание, он не будет иметь никаких преимуществ перед противником в раскрытии исходного текста M по известному C.
Атаки на криптосистему с открытым ключом аналогичны атакам на криптосистемы с секретным ключом, однако следует помнить, что в первом случае противник всегда знает открытый ключ, а значит, всегда возможна атака на основе выбранного открытого текста. Кроме того, возможна так называемая атака с проверкой текста (verifiable text attack): если число возможных открытых текстов невелико, противник, зная открытый ключ, может заранее заготовить соответствующие им шифротексты, а затем, сравнивая с ними перехваченные шифровки, получать соответствующие последним открытые тексты. Исключить такой вид атак на криптосистему позволяет вероятностное шифрование.
Шифрование с открытым ключом может использоваться в тех из рассмотренных в параграфе 3.5 режимах (например, ECB и CBC), которые для зашифрования и расшифрования используют разные функции, соответственно E и D.
Наиболее известные системы с открытым ключом:
- криптосистема RSA;
- криптосистема, основанная на свойствах эллиптических кривых (Elliptic Curve Cryptosystem (ECCS).
Криптосистема RSA, многолетний неофициальный стандарт на шифрование с открытым ключом, будет рассмотрена ниже. Краткие сведения о лучшей на сегодняшний день криптосистеме ECCS даны в Приложении 5. Именно эта система послужила основой для создания российского, немецкого и американского стандартов электронной подписи, о которой речь пойдет ниже.
3.6.3. Открытое распределение ключей
Помимо принципа построения асимметричных криптосистем Диффи и Хеллман предложили протокол выработки общего секретного ключа, т.е. процедуру взаимодействия по открытому каналу связи удаленных абонентов A и B, обладающую следующими свойствами:
- в конце процедуры у A и B появляется общая секретная информация (общий секретный ключ), которой до начала действия протокола не было;
- противник, который способен перехватывать все сообщения и знает цель протокола, не может восстановить сформированный секретный ключ.
Этот на первый взгляд невозможный протокол основывается на задаче дискретного логарифмирования, рассмотренной выше. Противник, который хочет узнать формируемый секретный ключ, вынужден решать именно эту трудную математическую задачу. Допустим, p - большое простое число, w - примитивный элемент поля GF (p). Числа p и w считаются общедоступными. Тогда процедура получения общей секретной информации имеет следующий вид.
Протокол выработки общего секретного ключа Диффи—Хеллмана.
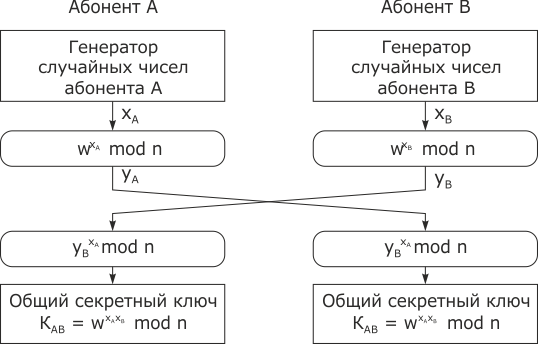
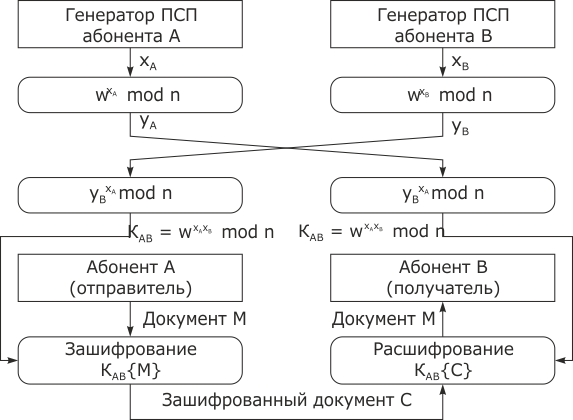
Первый вариант приведен на рис. 3.21.
- Абоненты A и B независимо друг от друга вырабатывают два случайных числа соответственно
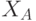 и
и 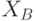 , которые держат в секрете.
, которые держат в секрете. - Абоненты A и B вычисляют значения
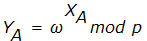 и
и 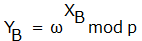
- Абоненты A и B обмениваются сообщениями
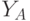 и
и 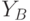 .
. - Абонент A, получив сообщение
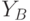 , вычисляет значение
абонент B, получив сообщение
, вычисляет значение
абонент B, получив сообщение 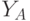 , вычисляет значение
, вычисляет значение
- Число, равное
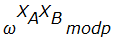 , объявляется общим секретным ключом
, объявляется общим секретным ключом 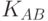 .
.
Второй вариант
- Абоненты A и B независимо друг от друга вырабатывают два случайных числа соответственно
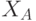 и
и 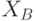 , которые держат в секрете.
, которые держат в секрете. - Абоненты A и B вычисляют значения
 и
и 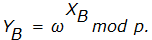
- Абоненты A и B публикуют соответственно
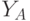 и
и 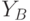 в качестве своих открытых ключей.
в качестве своих открытых ключей. - Абонент A для обмена секретными сообщениями с абонентом В использует общий секретный ключ абонент B для обмена секретными сообщениями с абонентом A использует общий секретный ключ
3.6.4. Электронная подпись
Одностороннюю функцию с секретом Диффи и Хеллман предложили использовать для электронной цифровой подписи сообщений, которая позволила бы, например, устанавливать истину при возникновении споров относительно авторства пересылаемых важных документов. Традиционная криптосистема с секретным ключом не может быть использована для разрешения противоречий, возникающих между не доверяющими друг другу абонентами, так как секретная информация (ключ), используемая для зашифрования сообщений, известна как минимум двум лицам. Поэтому пересылка по линиям связи платежных документов или информации, требующей нотариального заверения, в этом случае чревата большими неприятностями.
Если  - односторонняя функция с секретом, то подписанное сообщение можно представить в виде пары:
- односторонняя функция с секретом, то подписанное сообщение можно представить в виде пары:
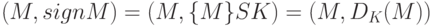 ,
,
| где | M | - | подписываемый документ, |
| sign M | - | подпись на документе М; | |
| SK | - | секретный ключ; | |
 |
- | функция, обратная  . . |
Из определения односторонней функции с секретом следует, что для такой подписи характерны следующие особенности:
- подписать сообщение M может только обладатель секретного ключа SK, т.е. подделать подпись практически невозможно;
- проверить подпись может любой абонент, знающий функцию
 и открытый ключ PK, так как проверка подписи заключается в проверке равенства
и открытый ключ PK, так как проверка подписи заключается в проверке равенства
или, что то же самое,
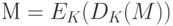 ;
; - при возникновении споров относительно авторства сообщений отказаться от подписи нельзя из-за невозможности ее подделки;
- подпись позволяет контролировать целостность подписанных документов, а значит, их можно безо всякого ущерба пересылать по открытым каналам связи.
Если необходимо обеспечить секретность, можно применить следующий протокол электронной цифровой подписи. Допустим, у двух абонентов A и B имеются взаимно обратные функции зашифрования E и расшифрования D и у каждого из них пара (открытый/закрытый) ключей - соответственно 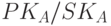 и
и 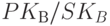 . Если абонент А хочет послать подписанное сообщение абоненту В, он, используя сначала свой секретный ключ, а затем открытый ключ получателя, вычисляет
. Если абонент А хочет послать подписанное сообщение абоненту В, он, используя сначала свой секретный ключ, а затем открытый ключ получателя, вычисляет
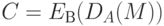 ,
,
| где | 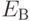 |
- | функция шифрования на открытом ключе абонента В; |
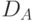 |
- | функция шифрования на секретном ключе абонента А, |
или

и передает шифротекст С абоненту B. Получатель сообщения, используя сначала свой секретный ключ, а затем открытый ключ абонента А, восстанавливает исходный текст, вычисляя
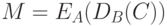 ,
,
| где | 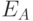 |
- | функция шифрования на открытом ключе абонента А; |
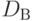 |
- | функция шифрования на секретном ключе абонента В, |
или
 .
.
Теперь при возникновении спорной ситуации, когда А отказывается от посланного сообщения, он обязан предъявить арбитру свой секретный ключ. Арбитру необходимо лишь проверить равенство
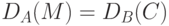 .
.
В случае его выполнения он убеждается, что никто, кроме А, отправить сообщение не мог, и принимает решение в пользу В.
Приведенный протокол заставляет быть честным и абонента В. Для того чтобы исказить принятое сообщение M на M`, ему необходимо изменить и подпись 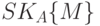 на
на 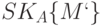 . Но для этой операции необходим секретный ключ
. Но для этой операции необходим секретный ключ 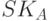 абонента А, которого у В нет.
абонента А, которого у В нет.
Приведенная последовательность применения функций 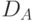 и
и 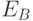 единственно возможна. Если абонент А попытается послать В "подписанное" сообщение вида
единственно возможна. Если абонент А попытается послать В "подписанное" сообщение вида
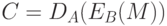
или
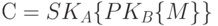 ,
,
противник W, перехватив это сообщение, используя открытый ключ абонента А, сможет вычислить 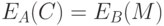 , а затем, используя свой закрытый ключ, послать якобы подписанное им сообщение
, а затем, используя свой закрытый ключ, послать якобы подписанное им сообщение
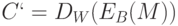 ,
,
или
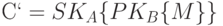 .
.
Тогда В, вычислив
 ,
,
был бы убежден, что M подписано именно W. Таким образом, в рассматриваемой ситуации противник всегда может подписывать сообщения, содержимое которых он сам прочитать не в состоянии.
Общий недостаток всех криптосистем с открытым ключом - низкое быстродействие, поэтому на практике применяются модифицированные схемы электронной подписи, в значительной степени решающие эту проблему, они будут рассмотрены в параграфе 3.10.
3.6.5. Криптосистема RSA
Система RSA, название которой происходит от первых букв фамилий авторов, Р. Ривеста, А. Шамира и Л. Адлемана (R. Rivest, A. Shamir, L. Adleman), является наиболее распространенной и изученной криптосистемой с открытым ключом. Она основана на использовании того факта, что легко перемножить два больших простых числа, в то же время крайне трудно разложить на множители их произведение. В результате произведение может быть использовано в качестве элемента открытого ключа зашифрования. Исходные простые числа необходимы для расшифрования, при этом задача их восстановления до сих пор сопротивляется всем атакам криптоаналитиков. Таким образом, имеются предпосылки для построения односторонней функции с секретом.
Выберем два больших различных простых числа p и q и число e, взаимно простое с числом 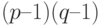 . Вычислим
. Вычислим  и найдем d, такое, при котором
и найдем d, такое, при котором
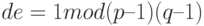 .
.
В результате для любого X < N будет справедливо:
 .
.
Тогда рассматриваемая криптосистема выглядит следующим образом.
Криптосистема RSA.
Открытый ключ зашифрования: числа N и e.
Закрытый ключ расшифрования: числа p, q и d.
Алгоритм зашифрования сообщения M:
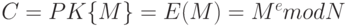 .
.
Алгоритм расшифрования закрытого сообщения C:
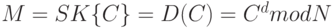 .
.
Единственный способ для противника найти алгоритм расшифрования D при известных e и N состоит в том, чтобы разложить на простые множители число N, найти p и q, а следовательно, и d. Правильный выбор разрядности чисел p и q (первоначально авторы RSA предлагали в качестве p и q использовать не менее чем 40-разрядные десятичные числа) делает задачу факторизации N практически неосуществимой.
Пример шифрования по приведенной схеме показан на рис. 3.22.
Авторы RSA при описании принципов функционирования своей системы выбрали в качестве исходного текста фразу
"ITS ALL GREEC TO ME" ("Для меня все это совершенно непонятно").
Для того чтобы преобразовать этот текст в одно большое число, закодировали пробел между словами 0, букву А - 1, букву В - 2, букву С - 3, ..., букву Z - 26. На представление каждого символа выделили пять двоичных разрядов. В результате приведенной фразе стало соответствовать число
M = 09201900011212000718050511002015001305.
Для шифрования авторы выбрали e = 9007 и
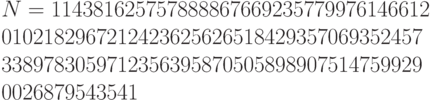
После зашифрования получили число
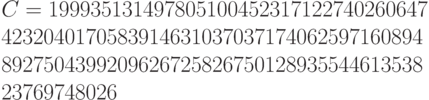
Число N было произведением 64-значного и 65-значного простых чисел p и q, выбранных случайным образом.
Если исходный текст слишком велик, чтобы с ним можно было обращаться как с одним числом, то его следует разбить на блоки и каждый блок рассматривать как отдельное число, при этом необходимо использовать шифрование со сцеплением блоков (режим CBC).
При разработке криптосистемы сначала выбираются два различных простых числа p и q. Для этого произвольно выбирается нечетное число r подходящего размера (например, сторазрядное) и проверяется на простоту. В случае если тест дает отрицательный результат, проверяется число r + 2 и т.д. Вероятность успеха одного конкретного теста проверки на простоту случайно выбранного числа равна приблизительно 0,00868. После того как p и q выбраны, кандидаты на e проверяются с помощью алгоритма Евклида. Когда e удовлетворяет условию (e, j (N)) = 1, т.е. числа e и j (N) = (p – 1) (q – 1) взаимно просты, цепочка равенств, получаемых в результате применения алгоритма Евклида, дает нам и значение d. Процедура шифрования суть модульное возведение в степень, эту операцию следует осуществлять методом последовательного возведения в квадрат, т.е. после каждого возведения в квадрат результат берется по модулю N.
При этом никогда не возникают числа большие 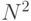 .
.
3.6.6. Гибридные криптосистемы
Несмотря на все преимущества криптосистем с открытым ключом, ни одна из известных на сегодняшний день их реализаций не может конкурировать по быстродействию с криптосистемами с секретным ключом. Так, например, быстродействие системы RSA в тысячи раз ниже быстродействия DES. В результате при шифровании длинных информационных последовательностей может случиться так, что применение асимметричного алгоритма недопустимо снижает скорость информационного обмена, а применение симметричного невозможно из-за отсутствия общего секретного ключа у участников этого обмена или по каким-то другим причинам. Выходом из этой ситуации является использование гибридной криптосистемы, оба варианта которой приведены на рис. 3.23 и 3.24.
В схеме, показанной на
рис.
3.23, на начальном этапе участники информационного обмена (абоненты А и В), используя протокол выработки общего секретного ключа, формируют общую секретную информацию (сеансовый ключ  ). На следующем этапе для обмена зашифрованными сообщения используется криптосистема с секретным ключом.
). На следующем этапе для обмена зашифрованными сообщения используется криптосистема с секретным ключом.
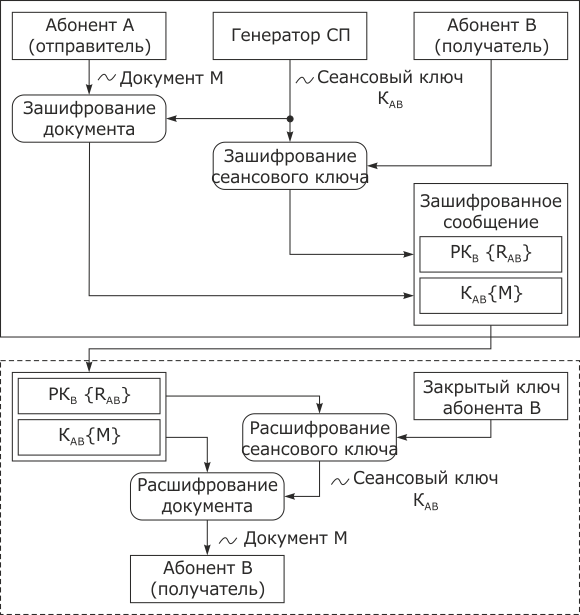
Схема, показанная на рис. 3.24, предполагает наличие у каждого участника информационного обмена двух ключей: открытого PK и закрытого SK. Рассмотрим процесс пересылки некоего документа M. Отправитель (абонент А) вырабатывает секретный ключ - случайное число, используемое только один раз и поэтому называемое одноразовым или сеансовым ключом. Этот ключ используется для зашифрования документа M при помощи симметричного криптоалгоритма. Сеансовый ключ зашифровывается на открытом ключе получателя (абонент В) и присоединяется к ранее зашифрованному документу. Сформированное таким образом сообщение отсылается получателю. Последний, получив сообщение, повторяет те же процедуры, но в обратном порядке. С помощью своего секретного ключа получатель восстанавливает сеансовый ключ, а затем с его помощью расшифровывает и сам документ.