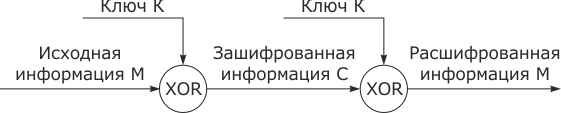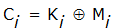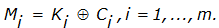| Россия, г. Туймазы |
Методы защиты информации в компьютерных системах и сетях
3.4. Криптографические методы защиты
3.4.1. Основные термины и определения
Современная криптография включает в себя следующие основные разделы:
- криптосистемы с секретным ключом (классическая криптография);
- криптосистемы с открытым ключом;
- криптографические протоколы.
Введем некоторые понятия, необходимые в дальнейшем:
| алфавит | - | конечное множество используемых для шифрования информации знаков; |
| текст | - | упорядоченный набор из элементов алфавита; |
| шифр | - | совокупность обратимых преобразований множества открытых данных на множество зашифрованных данных, заданных алгоритмом криптографического преобразования (криптоалгоритмом); |
| ключ | - | сменный элемент шифра, применяемый для закрытия отдельного сообщения, т.е. конкретное секретное состояние параметров криптоалгоритма, обеспечивающее выбор одного варианта преобразования из совокупности возможных; именно ключом определяется в первую очередь безопасность защищаемой информации и поэтому применяемые в надежных шифрах преобразования в большой степени зависят от ключа; |
| зашифрование | - | преобразование открытых данных в закрытые (зашифрованные) с помощью определенных правил, содержащихся в шифре; |
| расшифрование | - | обратный процесс; |
| шифрование | - | процесс зашифрования или расшифрования; |
| криптосистема | - | состоит из пространства ключей, пространства открытых текстов, пространства шифротекстов и алгоритмов зашифрования и расшифрования; |
| дешифрование | - | процесс преобразования закрытых данных в открытые при неизвестном ключе и (или) неизвестном алгоритме (вскрытие или взлом шифра); |
| синхропосылка | - | исходные параметры криптоалгоритма; |
| раскрытие криптоалгоритма | - | результат работы криптоаналитика, приводящий к возможности эффективного определения любого зашифрованного с помощью данного алгоритма открытого текста; |
| стойкость криптоалгоритма | - | способность шифра противостоять всевозможным попыткам его раскрытия, т.е. атакам на него. |
3.4.2. Оценка надежности криптоалгоритмов
Все современные шифры базируются на принципе Кирхгофа, согласно которому секретность шифра обеспечивается секретностью ключа, а не секретностью алгоритма шифрования. В некоторых ситуациях (например, в военных, разведывательных и дипломатических ведомствах) нет никаких причин делать общедоступным описание сути криптосистемы. Сохраняя такую информацию в тайне, можно дополнительно повысить надежность шифра. Однако полагаться на секретность этой информации не следует, так как рано или поздно она будет скомпрометирована. Поэтому анализ надежности таких систем всегда должен проводиться исходя из того, что противник имеет всю информацию о применяемом криптоалгоритме, ему неизвестен только реально использованный ключ. В связи с вышеизложенным можно сформулировать общее правило: при создании или при анализе стойкости криптосистем не следует недооценивать возможностей противника. Их лучше переоценить, чем недооценить.
Стойкость криптосистемы зависит от сложности алгоритмов преобразования, длины ключа, а точнее от объема ключевого пространства, метода реализации: при программной реализации необходимо дополнительно защищаться от разрушающих программных воздействий (вирусов, червей, троянских программ). Хотя понятие стойкости шифра является центральным в криптографии, количественная оценка криптостойкости - проблема до сих пор не решенная.
Методы оценки качества криптоалгоритмов, используемые на практике:
- всевозможные попытки их вскрытия;
- анализ сложности алгоритма дешифрования;
- оценка статистической безопасности шифра.
В первом случае многое зависит от квалификации, опыта, интуиции криптоаналитиков и от правильной оценки возможностей противника. Обычно считается, что противник знает шифр, имеет возможность его изучения, знает некоторые характеристики открытых защищаемых данных, например тематику сообщений, их стиль, стандарты, форматы и т.п.
Во втором случае оценку стойкости шифра заменяют оценкой минимальной сложности алгоритма его вскрытия. Однако получение строгих доказуемых оценок нижней границы сложности алгоритмов рассматриваемого типа проблематично. Иными словами, всегда возможна ситуация, когда алгоритм вскрытия шифра, сложность которого анализируется, оказывается вовсе не самым эффективным.
Сложность вычислительных алгоритмов можно оценивать числом выполняемых элементарных операций, при этом необходимо учитывать их стоимость и затраты на их выполнение. В общем случае это число должно иметь строгую нижнюю оценку и выходить за пределы возможностей современных компьютерных систем. Качественный шифр невозможно раскрыть способом более эффективным, нежели полный перебор по всему ключевому пространству, при этом криптограф должен рассчитывать только на то, что у противника не хватит времени и ресурсов, чтобы это сделать.
В третьем случае можно сформулировать следующие необходимые условия стойкости криптосистемы, проверяемые статистическими методами:
- должна отсутствовать статистическая зависимость между входной и выходной последовательностями;
- выходная последовательность по своим статистическим свойствам должна быть похожа на истинно случайную последовательность;
- при неизменной входной информационной последовательности незначительное изменение ключа должно приводить к непредсказуемому изменению выходной последовательности;
- при неизменном ключе незначительное изменение входной последовательности должно приводить к непредсказуемому изменению выходной последовательности;
- не должно быть зависимостей между ключами, последовательно используемыми в процессе шифрования.
Существует много различных криптоалгоритмов, при этом нет ни одного, подходящего для всех случаев. В каждой конкретной ситуации выбор криптоалгоритма определяется следующими факторами:
- особенностью защищаемой информации (документы, исходные тексты программ, графические файлы и т.п.);
- особенностями среды хранения или передачи информации;
- ценностью информации, характером защищаемых секретов, временем обеспечения секретности;
- объемами информации, скоростью ее передачи, степенью оперативности ее предоставления пользователю;
- возможностями собственников информации, владельцев средств сбора, обработки, хранения и передачи информации по ее защите;
- характером угроз, возможностями противника.
3.4.3. Классификация методов шифрования информации
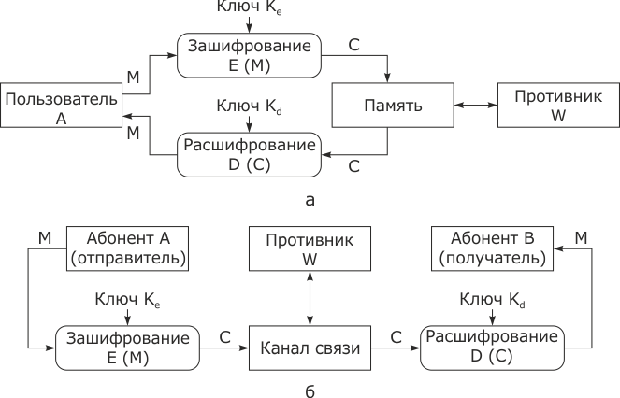
Основные объекты изучения классической криптографии показаны на рис. 3.4, где А и В - законные пользователи, W - противник или криптоаналитик. Учитывая что схема на рис. 3.4а фактически является частным случаем схемы на рис. 3.4б при В = А, в дальнейшем будет рассматриваться только она.
увеличить изображение
Рис. 3.4. Криптографическая защита: а - при хранении; б - при передаче информации по каналу связи
Процедуры зашифрования E (encryption) и расшифрования D (decryption) можно представить в следующем виде:


| где | M (message) и C (ciphertext) | - | открытый и зашифрованный тексты; |
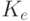 и и 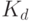
|
- | ключи зашифрования и расшифрования. |
Функции за- и расшифрования взаимно обратные, иначе говоря, для любого текста X справедливо:
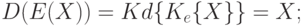
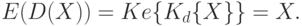
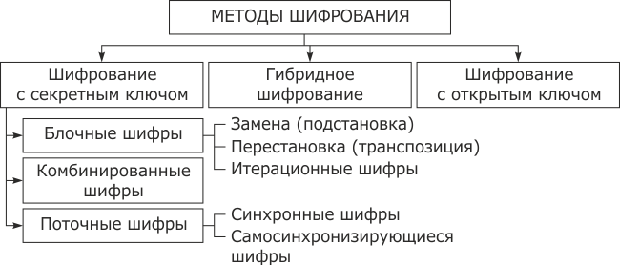
На рис. 3.5 приведена классификация методов шифрования информации. Различают два типа алгоритмов шифрования симметричные (с секретным ключом) и асимметричные (с открытым ключом). В первом случае обычно ключ расшифрования совпадает с ключом зашифрования, т.е.
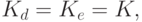
либо знание ключа зашифрования позволяет легко вычислить ключ расшифрования. В асимметричных алгоритмах такая возможность отсутствует: для зашифрования и расшифрования используются разные ключи, причем знание одного из них не дает практической возможности определить другой. Поэтому, если получатель А информации сохраняет в секрете ключ расшифрования 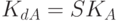 , ключ зашифрования
, ключ зашифрования 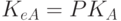 может быть сделан общедоступным (SK - secret key, PK - public key).
может быть сделан общедоступным (SK - secret key, PK - public key).
В процессе шифрования информация делится на порции величиной от одного до сотен бит. Как правило, поточные шифры оперируют с битами открытого и закрытого текстов, реже - с байтами, а блочные - с блоками фиксированной длины. Главное требование к блочному шифру - высокая криптостойкость. Блочный криптоалгоритм для своей работы требует наличия полного блока данных, в поточных же криптоалгоритмах стараются обеспечить шифрование в режиме рельного времени или близком к нему (иногда с ущербом для криптостойкости). Но главное различие между этими двумя методами заключается в том, что в блочных шифрах для шифрования всех порций используется один и тот же ключ, а в поточных - для каждой порции используется свой ключ той же размерности. Иначе говоря, в поточных шифрах имеет место зависимость результата шифрования порции информации от ее позиции в тексте, а в некоторых случаях и от результатов шифрования предыдущих порций текста. Таким образом, при реализации поточной криптосистемы возникает необходимость в элементах памяти, изменяя состояние которых, можно вырабатывать последовательность (поток) ключевой информации. Блочную же криптосистему можно рассматривать как зависящую от ключа замену на множестве значений блоков открытого текста.
Высокая скорость работы поточных шифров определяет область их использования - закрытие данных, требующих оперативной доставки потребителю, например аудио- и видеоинформации. Учитывая, что при применении классических блочных шифров одинаковым блокам открытого текста соответствуют одинаковые блоки шифротекста, что является серьезным недостатком, на практике получили наибольшее распространение комбинированные методы шифрования (а точнее, поточные режимы использования блочных шифров), использующие сцепление блоков или принцип формирования потока ключей (гаммы шифра) с помощью так называемых генераторов псевдослучайных последовательностей (ПСП), в качестве функции обратной связи которых используется функция зашифрования блочного шифра.
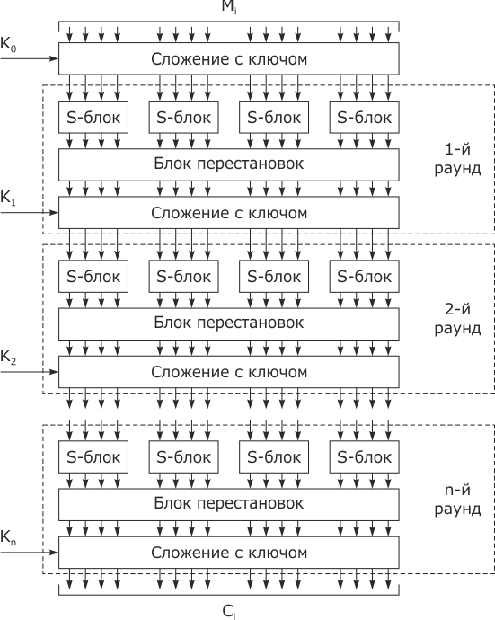
Блочные итерационные шифры. Принцип работы всех современных блочных шифров суть многократное повторение одной и той же раундовой операции. В некоторых случаях раундовые ключи получаются из ключа всей системы с помощью алгоритма выработки раундовых ключей (при этом размер ключа системы существенно меньше суммарного размера всех раундовых ключей).
Идея, лежащая в основе итерационных блочных шифров, состоит в построении криптостойкой системы путем многократного применения относительно простых криптографических преобразований, в качестве которых К. Шеннон предложил использовать преобразования замены (подстановки) (substitution) и перестановки (permutation); схемы, реализующие эти преобразования, называются SP-сетями. Действие таких шифров аналогично "алгоритму", к которому прибегают, когда месят тесто:
Многократное использование этих преобразований, приведенное на рис. 3.6, позволяет обеспечить два свойства, которые должны быть присущи стойким шифрам: рассеивание (diffusion) и перемешивание (confusion) информации.
Рассеивание и перемешивание предполагают:
- распространение влияния одного знака открытого текста, а также одного знака ключа на значительное количество знаков шифротекста;
- сложную зависимость между ключом и шифротекстом.
Наличие у шифра этих свойств:
- позволяет скрыть статистическую зависимость между знаками открытого текста, иначе говоря, перераспределить избыточность исходного языка посредством распространения ее на весь текст;
- не позволяет восстанавливать неизвестный ключ по частям;
- не позволяет на основе статистического анализа шифротекста получать информацию об использованном ключе.
Самые известные блочные шифры - DES (Data Encryption Standard), старый американский стандарт шифрования, созданный в 1974 г., де-факто многолетний неофициальный мировой стандарт шифрования; российский стандарт криптозащиты ГОСТ 28147-89 и новый американский стандарт шифрования AES (Advanced Encryption Standard), принятый в 2001 г. в результате многолетнего открытого международного конкурса.
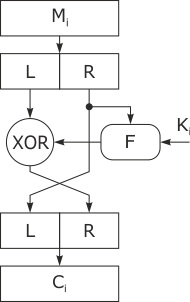
Структура раундового преобразования DES и ГОСТ носит название петли Фейстеля, схема которой приведена на рис. 3.7, а структура функций за- и расшифрования - сеть Фейстеля. Структура AES носит название "Квадрат".
DES работает с блоками данных разрядностью 64 бита с использованием 56-разрядного ключа, из которого по специальному фиксированному алгоритму, использующему перестановки и сдвиги, вырабатываются раундовые ключи. Применяемые преобразования - поразрядное сложение по модулю 2, подстановки и перестановки, число раундов равно 16, перед началом первого раунда выполняется начальная фиксированная перестановка IP, после 16-го раунда выполняется обратная перестановка 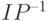 . Следуя рекомендациям Шеннона, в каждом раунде выполняется один шаг перемешивания (с использованием соответствующего раундового ключа и S-блоков (блоков замены), после которого следует шаг рассеивания, не зависящий от ключа.
. Следуя рекомендациям Шеннона, в каждом раунде выполняется один шаг перемешивания (с использованием соответствующего раундового ключа и S-блоков (блоков замены), после которого следует шаг рассеивания, не зависящий от ключа.
Интересно отметить, что в первоначальной схеме, предложенной IBM, все шестнадцать 48-разрядных раундовых ключей выбирались независимо, т.е. размер ключа был равен 768 битам. Однако по требованию Агентства национальной безопасности США (АНБ), во-первых, размер ключа был уменьшен до 64 бит, из которых только 56 являются секретными, во-вторых, в алгоритме определены перестановки лишь специального вида, не зависящие от ключа, что наводило критиков этого алгоритма на мысль, будто АНБ могла использовать известные ей слабости алгоритма для его взлома. На протяжении последних десятилетий DES подвергался интенсивному и всестороннему исследованию и по современным понятиям уже не считается надежным, в первую очередь из-за небольшой разрядности ключа.
Существует несколько предложений, направленных на усовершенствование DES. Наиболее известное из них, Triple DES, заключается в трехкратном применении алгоритма.
ГОСТ 28147-89. Ключевая информация ГОСТа представляет собой два массива данных: собственно ключ K и таблицу замен H. Ключ - это массив из восьми 32-разрядных элементов 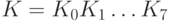 . Таким образом, размер ключа составляет 256 битов или 32 байта. Таблица замен - это набор из восьми одномерных массивов, так называемых узлов замены, каждый из которых определяет логику работы четырехразрядного блока подстановок (S-блока) и по этой причине содержит 16 четырехразрядных двоичных наборов (от 0 до 15), расположенных в произвольном порядке. Таким образом, объем таблицы замен равен 8 * 16 * 4 = 512 битов, или 64 байта. Таблица замен H в отличие от ключа К может являться долговременным ключевым элементом. Она, например, может быть общей для всех процедур шифрования в рамках одной системы криптографической защиты.
. Таким образом, размер ключа составляет 256 битов или 32 байта. Таблица замен - это набор из восьми одномерных массивов, так называемых узлов замены, каждый из которых определяет логику работы четырехразрядного блока подстановок (S-блока) и по этой причине содержит 16 четырехразрядных двоичных наборов (от 0 до 15), расположенных в произвольном порядке. Таким образом, объем таблицы замен равен 8 * 16 * 4 = 512 битов, или 64 байта. Таблица замен H в отличие от ключа К может являться долговременным ключевым элементом. Она, например, может быть общей для всех процедур шифрования в рамках одной системы криптографической защиты.
В качестве исходных данных раундовая функция шифрования ГОСТа получает 64-разрядный блок данных D = (L, R) и 32-разрядный раундовый ключ, в качестве которого используется один из элементов ключа Кi. В ходе выполнения преобразования левая L и правая R половины блока данных рассматриваются как отдельные 32-разрядные элементы данных, в качестве которых они подвергаются следующим преобразованиям:
- сложение по модулю
 полублока R и элементом ключа;
полублока R и элементом ключа; - разбиение результата S на восемь четырехбитовых блоков, поблочная замена по таблице замен, формирование из получившихся блоков нового значения S;
- циклический сдвиг результата S на 11 разрядов влево;
- поразрядное сложение по модулю 2 (XOR) результата S и полублока L;
- элемент R становится новым значением элемента L, значение результата предыдущей операции становится новым значением элемента R.
Полученные значения элементов L и R выдаются в качестве результата шага раундового преобразования.
ГОСТ 28147-89 определяет три режима шифрования данных (простая замена, гаммирование и гаммирование с обратной связью) и режим выработки имитоприставки (кода аутентификации сообщений).
3.4.4. Абсолютно стойкий шифр. Гаммирование
Простейшей и в то же время наиболее надежной из всех схем шифрования является так называемая схема однократного использования, приведенная на рис. 3.8, изобретение которой чаще всего связывают с именем Г.С. Вернама.
Формируется m-разрядная случайная двоичная последовательность - ключ шифра, известный отправителю и получателю сообщения. Отправитель производит побитовое сложение по модулю 2 ключа и m-разрядной двоичной последовательности, соответствующей пересылаемому сообщению:
| где |
 , , 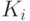 и и 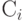
|
- | очередной i-й бит соответственно исходного сообщения, ключа и зашифрованного сообщения; |
| m | - | число битов открытого текста. |
Процесс расшифрования сводится к повторной генерации ключевой последовательности и наложения ее на зашифрованные данные. Уравнение расшифрования имеет вид:
К. Шенноном доказано, что, если ключ является фрагментом истинно случайной двоичной последовательностью с равномерным законом распределения, причем его длина равна длине исходного сообщения, и используется этот ключ только один раз, после чего уничтожается, такой шифр является абсолютно стойким, его невозможно раскрыть, даже если криптоаналитик располагает неограниченным запасом времени и неограниченным набором вычислительных ресурсов. Действительно, противнику известно только зашифрованное сообщение С, при этом все различные ключевые последовательности K возможны и равновероятны, а значит, возможны и любые сообщения M, т.е. криптоалгоритм не дает никакой информации об открытом тексте.
Целью противника может являться раскрытие криптосистемы, нахождение ключа, в крайнем случае, дешифрование какого-либо закрытого сообщения. Однако он может быть удовлетворен, получив даже некоторую вероятностную информацию об исходном тексте сообщения. Например, известный криптоаналитику факт написания текста некоторого сообщения на английском языке предоставляет ему некоторую априорную информацию об этом сообщении даже до анализа шифровки. В этом случае он заранее знает, что слово "HELLO" является более вероятным началом сообщения, чем набор букв "FGHKM". Поэтому одной из целей криптоанализа может являться увеличение информации, относящейся к каждому возможному сообщению таким образом, чтобы правильный текст был более вероятен. Предположим, противник перехватил шифровку "ABCCD" и знает (или предполагает), что использованный шифр - это шифр простой замены. Анализ шифровки позволяет сделать вывод, что исходное сообщение состоит из пяти букв, причем на третьей и четвертой позициях стоит одна и та же буква, а остальные отличны от нее и различны между собой. Противник не может считать, что это сообщение "HELLO", потому что имеются и другие возможные сообщения, например "TEDDY". Однако апостериорные вероятности таких открытых текстов возрастают относительно их априорных вероятностей. В то же время апостериорная вероятность таких открытых текстов, как "PEACE" или "GATES", снижается до нуля вне зависимости от их априорной вероятности. По К. Шеннону, в совершенно секретных криптосистемах после анализа закрытых текстов апостериорные вероятности возможных открытых текстов остаются такими же, какими были их априорные вероятности.
Необходимые и достаточные условия абсолютной стойкости шифра:
- полная случайность ключа;
- равенство длин ключа и открытого текста;
- однократное использование ключа.
Абсолютная стойкость рассмотренной схемы оплачивается слишком большой ценой, она чрезвычайно дорогая и непрактичная. Основной ее недостаток - это равенство объема ключевой информации и суммарного объема передаваемых сообщений. Применение схемы оправдано лишь в не часто используемых каналах связи для шифрования исключительно важных сообщений. Существует большое число модификаций представленной схемы, наиболее известная из которых основана на использовании одноразовых шифровальных блокнотов.
Таким образом, построить эффективный криптоалгоритм можно, лишь отказавшись от абсолютной стойкости. Возникает задача разработки такого теоретически нестойкого шифра, для вскрытия которого противнику потребовалось бы выполнить такое число операций, которое осуществимо на современных и ожидаемых в ближайшей перспективе вычислительных средствах за разумное время. В первую очередь следует иметь схему, которая использует ключ небольшой разрядности, в дальнейшем выполняющий функцию "зародыша", порождающего значительно более длинную ключевую последовательность.
Данный результат может быть достигнут при использовании гаммирования, схема которого показана на рис. 3.9.
Гаммированием называют процедуру наложения на входную информационную последовательность гаммы шифра, т.е. последовательности с выходов генератора псевдослучайных последовательностей (ПСП) G. Последовательность называется псевдослучайной, если по своим статистическим свойствам она неотличима от истинно случайной последовательности, но в отличие от последней является детерминированной, т.е. знание алгоритма ее формирования дает возможность ее повторения необходимое число раз. Если символы входной информационной последовательности и гаммы представлены в двоичном виде, наложение чаще всего реализуется с помощью операции поразрядного сложения по модулю 2. Надежность шифрования методом гаммирования определяется качеством генератора гаммы.
3.4.5. Генераторы псевдослучайных последовательностей
Качественные ПСП, являясь по своей сути детерминированными, успешно заменяют во многих приложениях (в первую очередь связанных с защитой информации) случайные последовательности, которые чрезвычайно сложно формировать.
Можно выделить следующие задачи, требующие решения при организации защиты информационных систем:
- обеспечение работоспособности компонентов и системы в целом при наличии случайных и умышленных деструктивных воздействий;
- обеспечение секретности и конфиденциальности информации или наиболее важной ее части;
- защита от НСД;
- обеспечение аутентичности информации (целостности, подлинности и пр.);
- обеспечение аутентичности участников информационного обмена;
- обеспечение юридической значимости пересылаемых электронных документов;
- обеспечение неотслеживаемости информационных потоков в системе;
- защита прав собственников информации.
Во всех рассмотренных случаях генераторы ПСП применяются либо непосредственно, либо косвенно, когда на их основе строятся генераторы случайных последовательностей, генераторы контрольных кодов и хеш-генераторы. Во всех случаях требуются последовательности с равномерным законом распределения.
Можно выделить следующие функции генераторов ПСП в системах защиты информации:
- формирование гаммы при шифровании информации в режимах гаммирования и гаммирования с обратной связью;
- формирование ключей и паролей пользователей;
- формирование случайных запросов при аутентификации удаленных абонентов;
- формирование затемняющих множителей при слепом шифровании;
- формирование контрольных кодов целостности информации;
- хеширование информации при организации парольных систем, построении протоколов электронной подписи, аутентификации по принципу запрос-ответ и др.
Требования к качественному генератору ПСП:
- непредсказуемость;
- определенные статистические свойства;
- большой период формируемых последовательностей;
- эффективная реализация.
Непредсказуемость. Данное требование означает, что для противника, имеющего возможность анализировать фрагмент ПСП конечной длины, три задачи вычислительно неразрешимы:
- предсказание следующего элемента последовательности;
- определение предыдущего элемента последовательности;
- определение использованной при генерации ключевой информации.
В первых двух случаях самая эффективная возможная стратегия - бросание жребия, в третьем - полный перебор по всему ключевому пространству.
Определенные статистические свойства. Это требование означает, что ни один из существующих статистических тестов не в состоянии обнаружить на выходе генератора какие-либо закономерности статистических зависимостей между различными последовательностями, формируемыми при инициализации генератора случайными значениями.
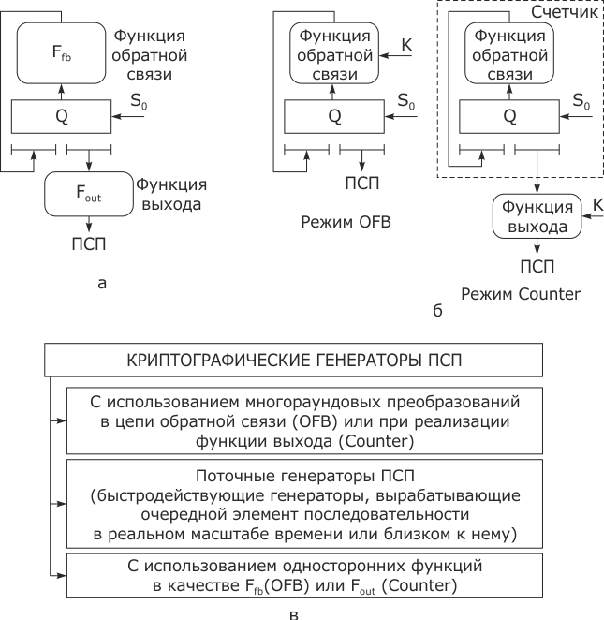
Принципы построения генераторов ПСП. Можно выделить два подхода при использовании в составе генераторов ПСП нелинейных функций: это использование нелинейной функции непосредственно в цепи обратной связи и двухступенчатая схема, в которой задача первой ступени (по сути счетчика) заключается всего лишь в обеспечении максимально большого периода при данном числе N элементов памяти Q. Во втором случае нелинейная функция является функцией выхода  . На
рис.
3.10 представлены обе вышеназванные схемы.
. На
рис.
3.10 представлены обе вышеназванные схемы.
увеличить изображение
Рис. 3.10. Генераторы ПСП: а - общая схема; б - частные случаи (режимы OFB и Counter); в - классификация криптографических генераторов ПСП
Вторую схему следует считать более предпочтительной, так как первая имеет следующие недостатки:
- преобразование
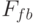 является двухпараметрическим, при этом нет никакой гарантии, что при всех значениях секретного параметра K (ключа) формируемая последовательность будет иметь достаточно большой период;
является двухпараметрическим, при этом нет никакой гарантии, что при всех значениях секретного параметра K (ключа) формируемая последовательность будет иметь достаточно большой период; - при возникновении ошибки на каком-то шаге выполнения нелинейного преобразования
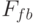 искажаются все последующие элементы ПСП.
искажаются все последующие элементы ПСП.
На
рис.
3.10в показана классификация криптографических генераторов ПСП. Роль нелинейных функций  или
или 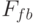 в рассматриваемой ситуации выполняет функция зашифрования E одноключевой (с секретным ключом) или двухключевой (с открытым ключом) криптосистемы. Непредсказуемость криптографических генераторов основывается на предположениях о том, что у аналитика не хватит ресурсов (вычислительных, временных или стоимостных) для того, чтобы инвертировать нелинейную функцию обратной связи или нелинейную функцию выхода генератора ПСП.
в рассматриваемой ситуации выполняет функция зашифрования E одноключевой (с секретным ключом) или двухключевой (с открытым ключом) криптосистемы. Непредсказуемость криптографических генераторов основывается на предположениях о том, что у аналитика не хватит ресурсов (вычислительных, временных или стоимостных) для того, чтобы инвертировать нелинейную функцию обратной связи или нелинейную функцию выхода генератора ПСП.
По совокупности вышеперечисленных требований наиболее приемлемое решение - генераторы ПСП, использующие многораундовые преобразования при построении функций  или
или 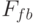 .
.
Наиболее обоснованными математически следует признать генераторы с использованием односторонних функций. Непредсказуемость данных генераторов основывается на сложности решения ряда математических задач (например, задачи дискретного логарифмирования или задачи разложения больших чисел на простые множители). Существенным недостатком генераторов этого класса является низкая производительность.
3.4.6. Поточные шифры
Шифр Вернама можно считать исторически первым поточным шифром. Так как поточные шифры в отличие от блочных осуществляют поэлементное шифрование потока данных без задержки в криптосистеме, их важнейшим достоинством является высокая скорость преобразования, соизмеримая со скоростью поступления входной информации. Таким образом обеспечивается шифрование практически в реальном масштабе времени вне зависимости от объема и разрядности потока преобразуемых данных.
В синхронных поточных шифрах (см. рис. 3.9) гамма формируется независимо от входной последовательности, каждый элемент (бит, символ, байт и т.п.) которой таким образом шифруется независимо от других элементов. В синхронных поточных шифрах отсутствует эффект размножения ошибок, т.е. число искаженных элементов в расшифрованной последовательности равно числу искаженных элементов зашифрованной последовательности, пришедшей из канала связи. Вставка или выпадение элемента зашифрованной последовательности недопустимы, так как из-за нарушения синхронизации это приведет к неправильному расшифрованию всех последующих элементов.
В самосинхронизирующихся поточных шифрах осуществляется гаммирование с обратной связью - гамма зависит от открытого текста, иначе говоря, результат шифрования каждого элемента зависит не только от позиции этого элемента (как это происходит в случае синхронного поточного шифрования), но и от значения всех предыдущих элементов открытого текста. Свойство самосинхронизации объясняется отсутствием обратной связи на принимающей стороне, в то время как в случае синхронного поточного шифрования схемы за- и расшифрования абсолютно идентичны.