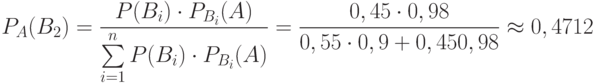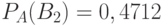Формула Байеса. Вероятность оценки гипотез
Основные теоретические сведения
Пусть событие А может наступить лишь при условии появления одного из несовместных событий (гипотез) 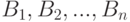 которые образуют полную группу событий. Если событие А уже произошло, то вероятности гипотез могут быть переоценены по формуле Байеса:
которые образуют полную группу событий. Если событие А уже произошло, то вероятности гипотез могут быть переоценены по формуле Байеса:
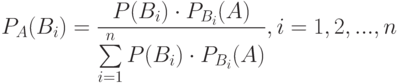 |
( 1.18) |
где  – вероятность события
– вероятность события  ,
, 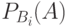 – условная вероятность события А, вычисленная при условии, что событие
– условная вероятность события А, вычисленная при условии, что событие  наступило;
наступило; 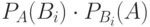 – вероятность события A;
– вероятность события A; 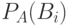 – условная вероятность события
– условная вероятность события  вычисленная при условии, что событие А произошло.
вычисленная при условии, что событие А произошло.
Формулы Бейеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.
Пример решения задачи
Задача: Изделие проверяется на стандартность одним из двух товароведов. Вероятность того, что изделие попадет к первому товароведу, равна 0,55, а ко второму – 0,45. Вероятность того, что стандартное изделие будет признано стандартным первым товароведом, равна 0,9, а вторым – 0,98. Стандартное изделие при проверке было признано стандартным. Найти вероятность того, что его проверил второй товаровед.

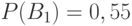
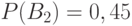
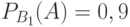
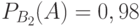
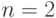
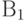 – изделие проверил первый товаровед
– изделие проверил первый товаровед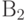 – изделие проверил первый товаровед
– изделие проверил первый товаровед