| Россия |
Анализ потока управления
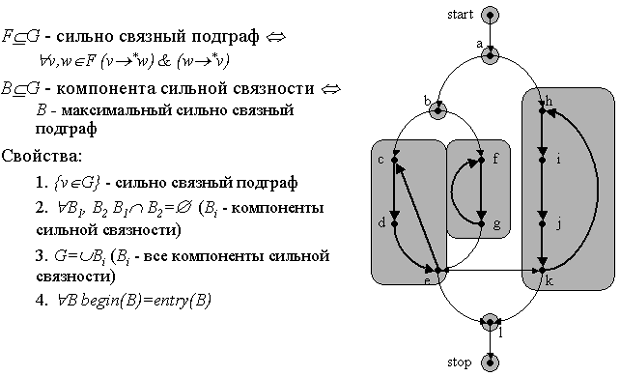
Сильно связный подграф
Сильно связный подграф - это фрагмент, состоящий из взаимно достижимых вершин. Компонента сильной связности - это максимальный сильно связный подграф.
Очевидно, произвольная вершина является сильно связным подграфом. Кроме того, легко показать, что множество компонент сильной связности задает разбиение множества вершин. Это разбиение показано на слайде.
Наконец, множества входных и начальных вершин для компонент сильной связности совпадают.
Как было показано в "Оптимизация" , выделение сильно связных подграфов имеет определяющее значение для реализации чистки циклов.
Выделение сильно связных подграфов (1)
Для выделения сильно связных подграфов введем понятие области при нумерации #, а именно, областью вершины v при нумерации # назовем множество вершин с большими номерами, из которых v достижима в подграфе, состоящем из всех вершин с большими номерами.
Можно показать, что область произвольной вершины при нумерации Post сильно связна.
Выделение сильно связных подграфов (2)
Для выделения сильно связных подграфов, таким образом, достаточно научиться выделять области. Заметим, однако, что, несмотря на то, что области при нумерации Post сильно связны, это не означает, что произвольные сильно связные подграфы будут областями при нумерации Post .
Алгоритм построения области приведен на слайде. Видно, что он осуществляет движение от текущей вершины по встречным дугам, проходя только по вершинам, имеющим большие номера, чем данная, и включает их в область.
Примеры подграфов, выделенных с помощью алгоритма, приведены на иллюстрации. Стрелочками отмечены вершины, области которых выделены.