Анализ потока управления

Построение глубинного остовного дерева

На слайде приведен алгоритм построения остовного дерева, определения типов дуг графа по отношению к нему и построения нумераций Pre и Post .

Алгоритм обходит вершины графа, начиная со start . При входе в очередную вершину ей присваивается очередной номер нумерации Pre , при этом номера Pre присваиваются в порядке возрастания. Далее рассматриваются все потомки этой вершины, которые еще не рассматривались. К каждому потомку применяется этот же самый шаг алгоритма - таким образом, обеспечивается обход в глубину. Наконец, после рассмотрения всех потомков текущей вершины ей присваивается очередной номер нумерации Post . При этом номера Post присваиваются в порядке убывания.

По ходу работы алгоритма поддерживается три состояния вершин:

• Init - вершина еще не рассматривалась алгоритмом
• InProcess - вершина еще рассматривается алгоритмом (т.е. алгоритм находится в процессе обработки вершин, достижимых из данной)
• Done - вершина уже исключена из рассмотрения (т.е. все достижимые из нее вершины уже обработаны).

Для определения типа дуги используется состояние конечной вершины и нумерация Pre . Если вершина, в которую можно попасть из данной, еще не рассматривалась, то ребро, по которому в нее можно попасть, объявляется деревянным. Для определения остальных типов дуг используются следующие очевидные утверждения:

• если в дуге (v, w) w находится в состоянии InProcess, то эта дуга - обратная
• если в дуге (v, w) w находится в состоянии Done, и Pre(w)<Pre(v), то эта дуга - поперечная
• если в дуге (v, w) w находится в состоянии Done, и Pre(w)>Pre(v), то эта дуга - прямая

Пример

увеличить изображение

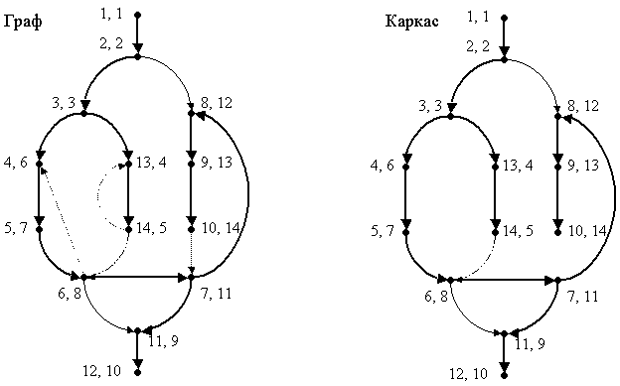
На слайде приведен пример графа потока управления и одного из его глубинных остовных деревьев. Каждая вершина помечена парой номеров, первый из которых соответствует нумерации Pre, а второй - нумерации Post . Деревянные дуги показаны толстыми линиями, прямые - тонкими, пунктирными линиями показаны обратные дуги и штрих-пунктирной - единственная поперечная дуга.

Граф, полученный удалением обратных по отношению к остовному дереву дуг, называется каркасом (показан в правой части слайда). Можно показать, что каркас графа при произвольном глубинном остовном дереве не содержит контуров.

Простейшие свойства

Граф называется сводимым тогда и только тогда, когда множество обратных дуг совпадает с множеством обратных дуг относительно глубинного остовного дерева для любого такого дерева.

Простейшие свойства нумераций Pre и Post:

• если вершина v обязательно предшествует вершине w , то Pre(v)<Pre(w), Post(v)<Post(w)
• прямые в смысле нумерации Pre дуги являются прямыми или деревянными относительно дерева
• обратные в смысле нумерации Pre дуги являются обратными или поперечными относительно дерева
• обратные в смысле нумерации Post дуги являются обратными в смысле дерева; остальные дуги являются прямыми относительно нумерации Post
• если Pre(v)>Pre(w) , то произвольный путь в графе от v до w содержит общего предка v и w в дереве
• граф сводим тогда и только тогда, когда отношение обязательного предшествования в нем и его каркасе совпадают

Сводимость является одной из основных характеристик графов потока управления. Как видно из определения, в сводимом графе обратные дуги для произвольного остовного дерева совпадают с обратными дугами относительно обязательного предшествования. Учитывая, что каждая обратная дуга определяет в графе потока управления контур (т.е. является абстракцией циклических конструкций языков программирования), циклическая структура сводимого графа является более регулярной, что упрощает анализ его свойств.