| Россия |
Анализ потока управления
Обязательное предшествование
Вершина v обязательно предшествует вершине w , если v принадлежит каждому пути в графе от start до w . В частности, любая вершина обязательно предшествует себе самой. Отношение обязательного предшествования будем обозначать символом ' < '. Легко видеть, что это отношение рефлексивно и транзитивно, но не симметрично. Таким образом, отношение обязательного предшествования задает частичный порядок на множестве вершин графа.
Вершина v строго обязательно предшествует вершине w , если она обязательно ей предшествует, но не совпадает с ней. Отношение строгого обязательного предшествования будем обозначать символом sdom .
Вершина v непосредственно предшествует вершине w , если она является ближайшей к w вершиной, которая ей строго предшествует.
Можно показать, что множество строгих обязательных предшественников для данной вершины линейно упорядочено, а непосредственный предшественник - это максимальный элемент в этом множестве. Таким образом, отношение непосредственного предшествования - это дерево. Легко показать, что корнем этого дерева является start .
Дуга (v, w) называется обратной в том и только том случае, когда w<v .
Отношение обязательного предшествования играет чрезвычайно важную роль в задачах анализа потока управления. Например, с его помощью могут быть решены задачи проверки сводимости (см. ниже), построения статической формы единственного присваивания (в этой лекции не рассматривается) и т.д.
Пример
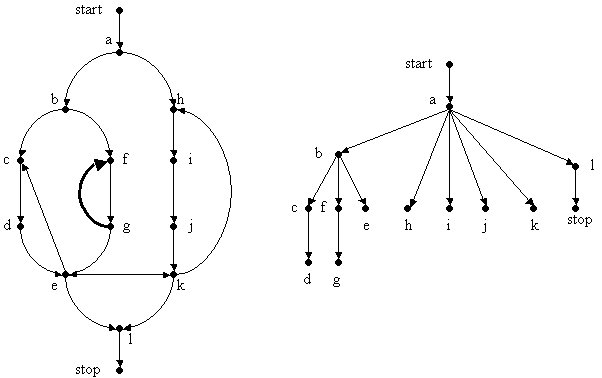
На слайде приведен пример графа потока управления и соответствующего ему дерева непосредственного предшествования. Дуга (g, f) является обратной.
Глубинное остовное дерево
Нумерацией называется взаимно однозначное отображение множества вершин графа на отрезок натурального ряда [1..|V|]. Для заданной нумерации # дуга (v, w) - прямая, если #(v)<#(w) и обратная в противном случае.
Остовное дерево - это дерево, содержащее все вершины графа и некоторые его дуги. Глубинное остовное дерево - это остовное дерево, полученное при обходе в глубину. Данный обход начинается в вершине start и заключается в последовательном включении вершин и ребер графа в дерево, если их еще там нет. При этом следующий сын вершины посещается лишь тогда, когда посещены все вершины, достижимые из предыдущего сына вершины.
Существует четыре типа дуг графа по отношению к данному глубинному остовному дереву: деревянные, прямые, обратные и поперечные. Следует отличать просто обратные дуги в графе (для определения которых было использовано отношение обязательного предшествования) и обратные дуги по отношению к глубинному остовному дереву.
- К деревянным относятся те дуги, которые входят в состав остовного дерева.
- К прямым дугам относятся те, чей конец достижим из начала в остовном дереве.
- К обратным дугам относятся те, чье начало достижимо из конца в остовном дереве.
- К поперечным дугам относятся все остальные.
Легко видеть, что при построении остовного дерева возникает порядок, в котором вершины графа включаются в рассмотрение. Нумерация, которая описывает этот порядок, называется прямой ( Pre ).
Аналогично, существует порядок, в котором вершины графа исключаются из рассмотрения. Нумерация, описывающая порядок, обратный к нему, называется обратной ( Post ).